Category: perception

Turn it down half-way…

#81 in a series of articles about the technology behind Bang & Olufsen loudspeakers

Bertrand Russell once said, “In all affairs it’s a healthy thing now and then to hang a question mark on the things you have long taken for granted.”

This article is a discussion, both philosophical and technical about what a volume control is, and what can be expected of it. This seems like a rather banal topic, but I find it surprising how often I’m required to explain it.

Why am I writing this?

I often get questions from colleagues and customers that sound something like the following:

  • Why does my Beovision television’s volume control only go to 90%? Why can’t I go to 100%?
  • I set the volume on my TV to 40, so why is it so quiet (or loud)?

The first question comes from people who think that the number on the screen is in percent – but it’s not. The speedometer in your car displays your speed in kilometres per hour (km/h), the tachometer is in revolutions of the engine per minute (RPM) the temperature on your thermostat is in degrees Celsius (ºC), and the display on your Beovision television is on a scale based on decibels (dB). None of these things are in percent (imagine if the speed limit on the highway was 80% of your car’s maximum speed… we’d have more accidents…)

The short reason we use decibels instead of percent is that it means that we can use subtraction instead of division – which is harder to do. The shortcut rule-of-thumb to remember is that, every time you drop by 6 dB on the volume control, you drop by 50% of the output. So, for example, going from Volume step 90 to Volume step 84 is going from 100% to 50%. If I keep going down, then the table of equivalents looks like this:

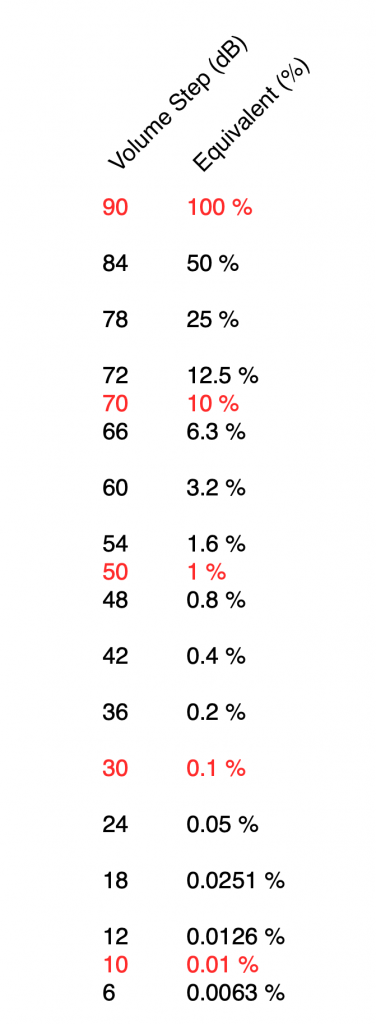
I’ve used two colours there to illustrate two things:

  • Every time you drop by 6 volume steps, you cut the percentage in half. For example, 60 is five drops of 6 steps, which is 1/2 of 1/2 of 1/2 of 1/2 of 1/2 of 100%, or 3.2% (notice the five halves there…)
  • Every time you drop by 20, you cut the percentage to 1/10. So, Volume Step 50 is 1% of Volume Step 90 because it’s two drops of 20 on the volume control.

If I graph this, showing the percentage equivalent of all 91 volume steps (from 0 to 90) then it looks like this:

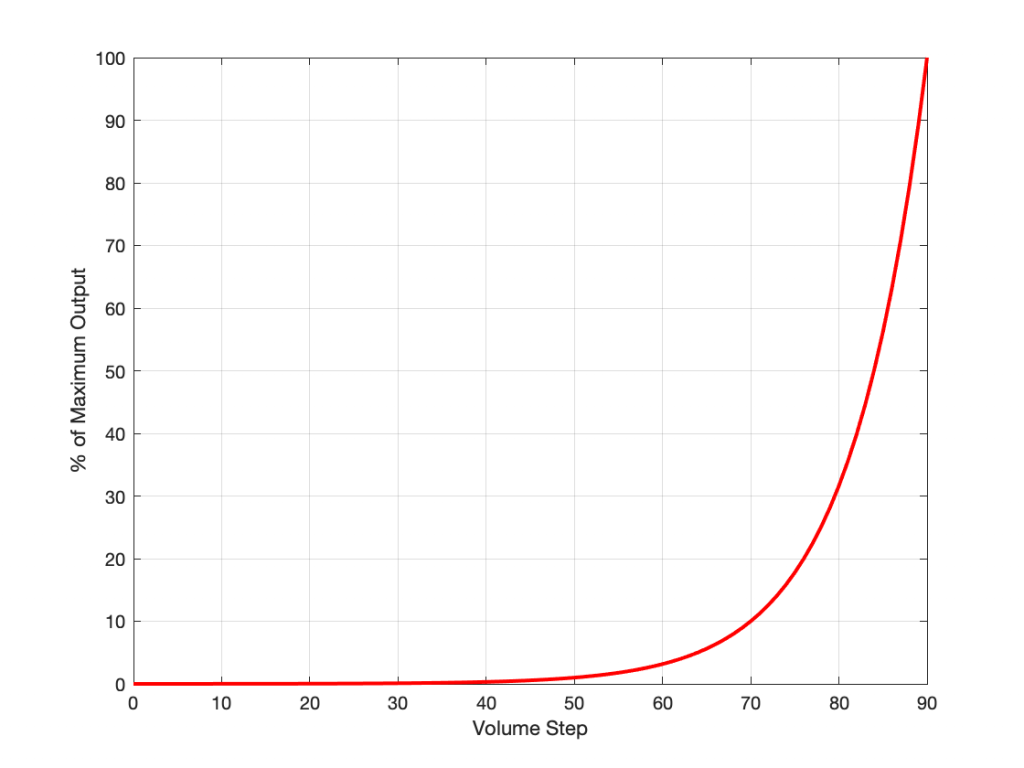
Of course, the problem this plot is that everything from about Volume Step 40 and lower looks like 0% because the plot doesn’t have enough detail. But I can fix that by changing the way the vertical axis is displayed, as shown below.

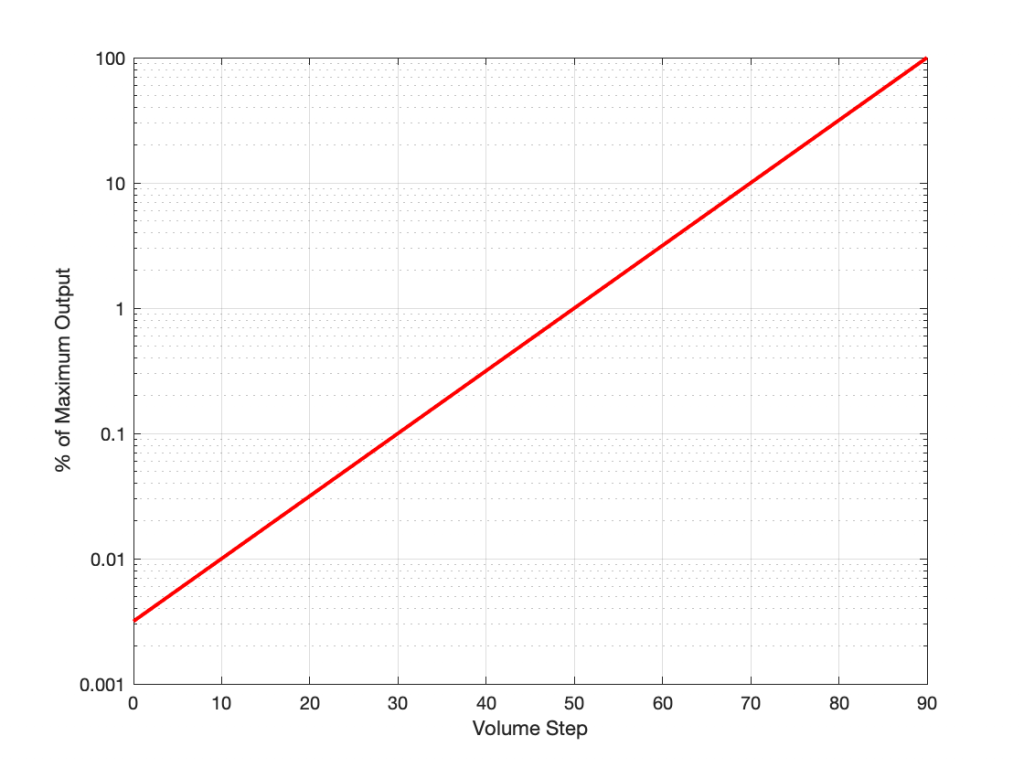
That plot shows exactly the same information. The only difference is that the vertical scale is no longer linearly counting from 0% to 100% in equal steps.

Why do we (and every other audio company) do it this way? The simple reason is that we want to make a volume slider (or knob) where an equal distance (or rotation) corresponds to an equal change in output level. We humans don’t perceive things like change in level in percent – so it doesn’t make sense to use a percent scale.

For the longer explanation, read on…

Basic concepts

We need to start at the very beginning, so here goes:

Volume control and gain

  1. An audio signal is (at least in a digital audio world) just a long list of numbers for each audio channel.
  2. The level of the audio signal can be changed by multiplying it by a number (called the gain).
    1. If you multiply by a value larger than 1, the audio signal gets louder.
    2. If you multiply by a number between 0 and 1, the audio signal gets quieter.
    3. If you multiply by zero, you mute the audio signal.
  3. Therefore, at its simplest core, a volume control implemented in a digital audio system is a multiplication by a gain. You turn up the volume, the gain value increases, and the audio is multiplied by a bigger number producing a bigger result.

That’s the first thing. Now we move on to how we perceive things…

Perception of Level

Speaking very generally, our senses (that we use to perceive the world around us) scale logarithmically instead of linearly. What does this mean? Let’s take an example:

Let’s say that you have $100 in your bank account. If I then told you that you’d won $100, you’d probably be pretty excited about it.

However, if you have $1,000,000 in your bank account, and I told you that you’re won $100, you probably wouldn’t even bother to collect your prize.

This can be seen as strange; the second $100 prize is not less money than the first $100 prize. However, it’s perceived to be very different.

If, instead of being $100, the cash prize were “equal to whatever you have in your bank account” – so the person with $100 gets $100 and the person with $1,000,000 gets $1,000,000, then they would both be equally excited.

The way we perceive audio signals is similar. Let’s say that you are listening to a song by Metallica at some level, and I ask you to turn it down, and you do. Then I ask you to turn it down by the same amount again, and you do. Then I ask you to turn it down by the same amount again, and you do… If I were to measure what just happened to the gain value, what would I find?

Well, let’s say that, the first time, you dropped the gain to 70% of the original level, so (for example) you went from multiplying the audio signal by 1 to multiplying the audio signal by 0.7 (a reduction of 0.3, if we were subtracting, which we’re not). The second time, you would drop by the same amount – which is 70% of that – so from 0.7 to 0.49 (notice that you did not subtract 0.3 to get to 0.4). The third time, you would drop from 0.49 to 0.343. (not subtracting 0.3 from 0.4 to get to 0.1).

In other words, each time you change the volume level by the “same amount”, you’re doing a multiplication in your head (although you don’t know it) – in this example, by 0.7. The important thing to note here is that you are NOT subtracting 0.3 from the gain in each of the above steps – you’re multiplying by 0.7 each time.

What happens if I were to express the above as percentages? Then our volume steps (and some additional ones) would look like this:

100%
70%
49%
34%
24%
17%
12%
8%

Notice that there is a different “distance” between each of those steps if we’re looking at it linearly (if we’re just subtracting adjacent values to find the difference between them). However, each of those steps is a reduction to 70% of the previous value.

This is a case where the numbers (as I’ve expressed them there) don’t match our experience. We hear each reduction in level as the same as the other steps, but they don’t look like they’re the same step size when we write them all down the way I’ve done above. (In other words, the numerical “distance” between 100 and 70 is not the same as the numerical “distance” between 49 and 34, but these steps would sound like the same difference in audio level.)

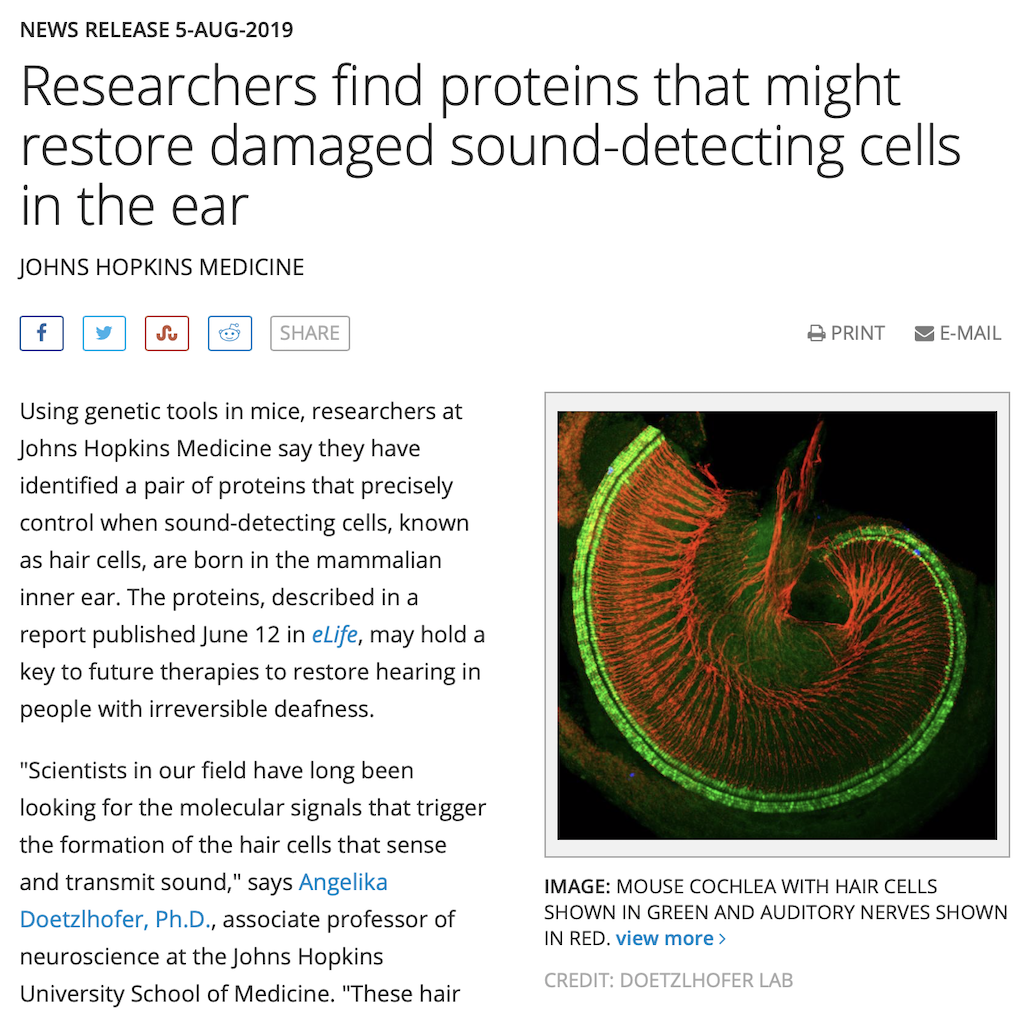
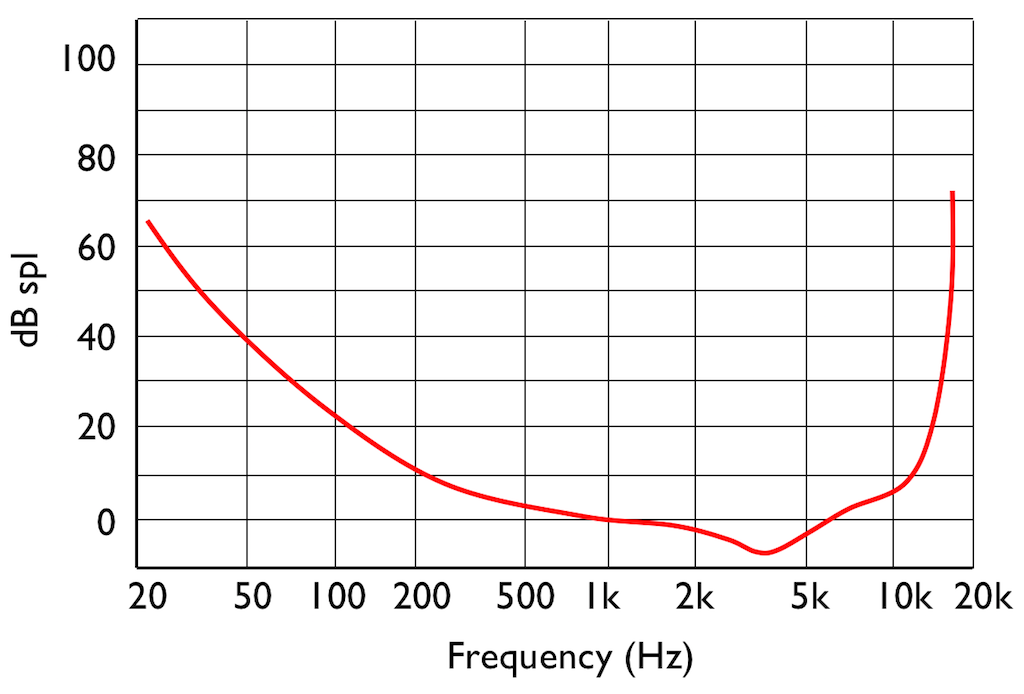
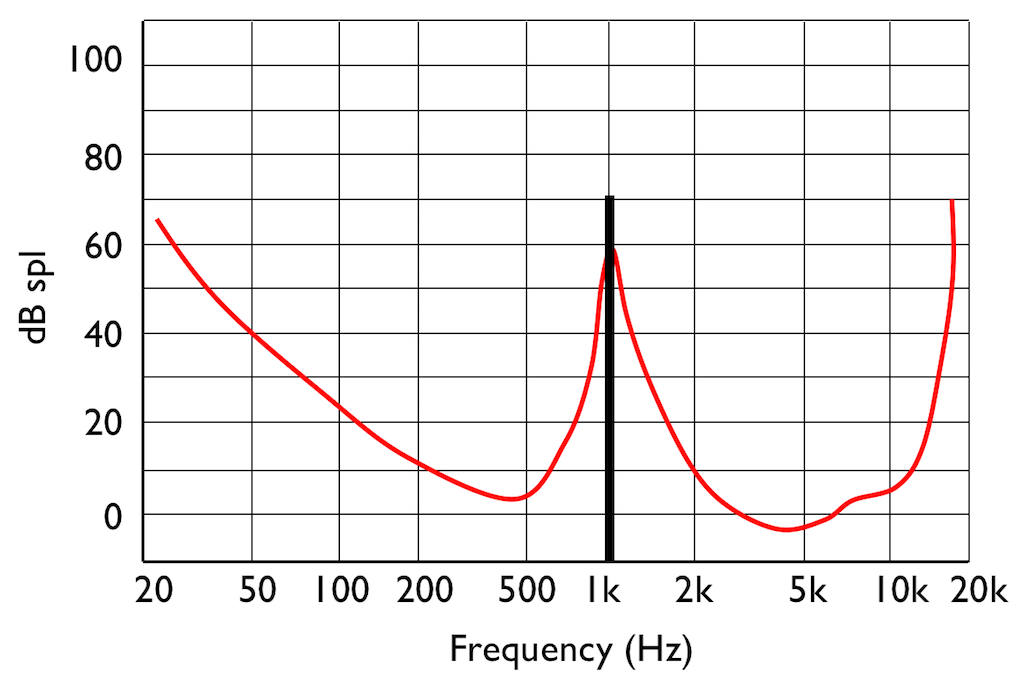
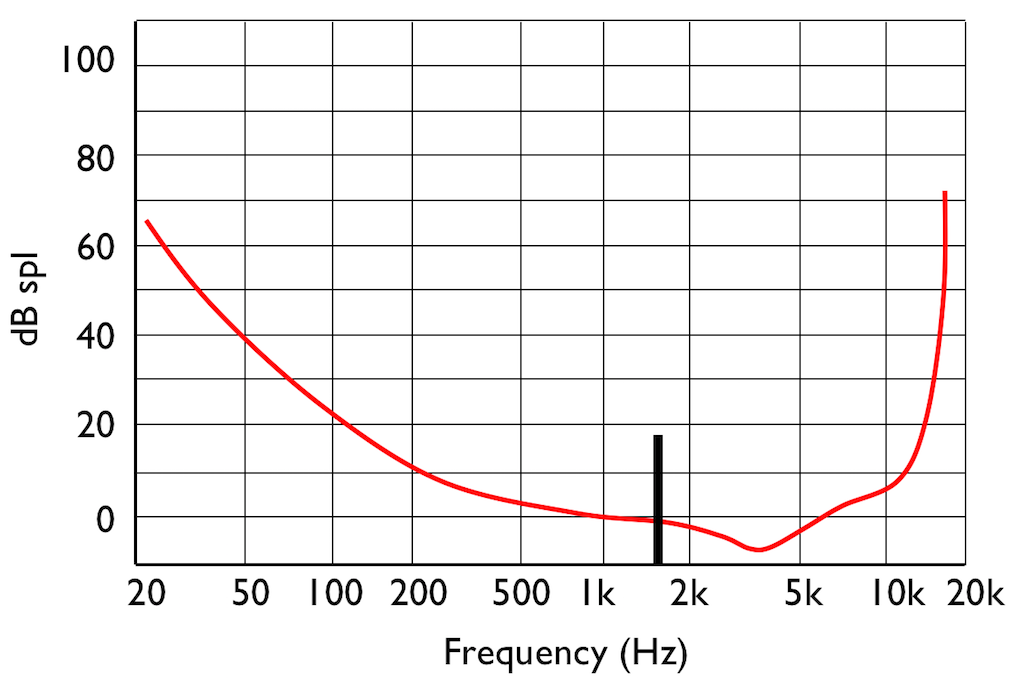
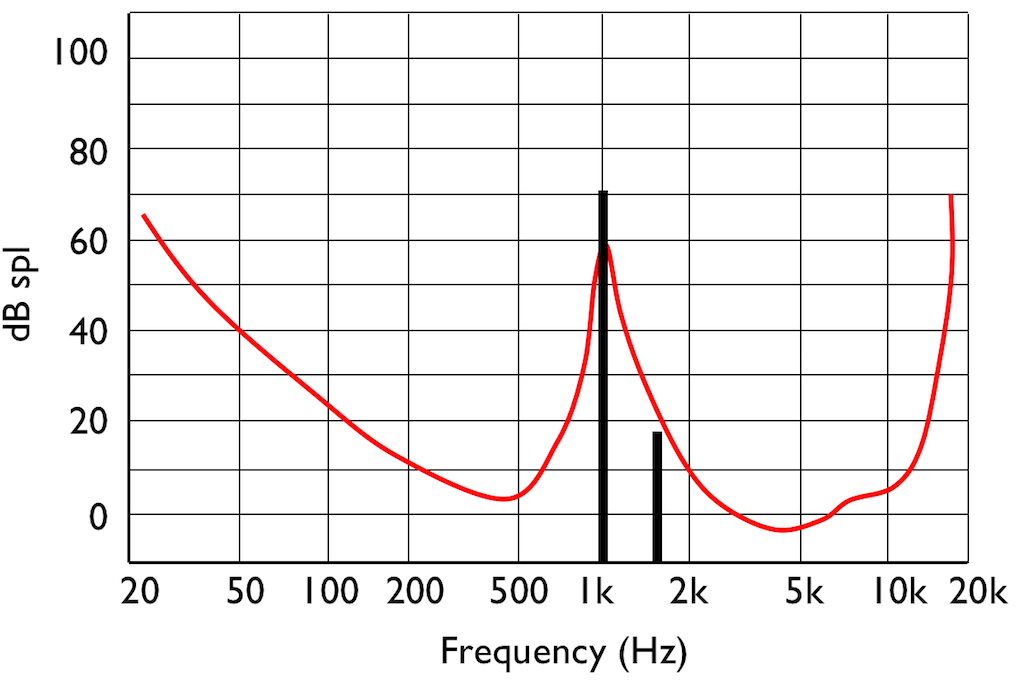
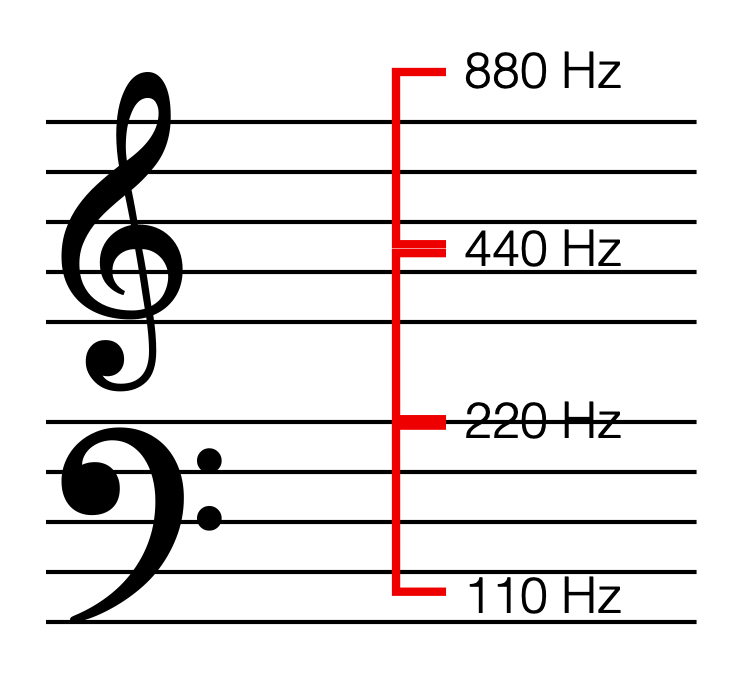
SIDEBAR: This is very similar / identical to the way we hear and express frequency changes. For example, the figure below shows a musical staff. The red brackets on the left show 3 spacings of one octave each; the distance between each of the marked frequencies sound the same to us. However, as you can see by the frequency indications, each of those octaves has a very different “width” in terms of frequency. Seen another way, the distance in Hertz in the octave from 440 Hz to 880 Hz is equal to the distance from 440 Hz all the way down to 0 Hz (both have a width of 440 Hz). However, to us, these sound like very different intervals.

SIDEBAR to the SIDEBAR: This also means that the distance in Hertz covered by the top octave on a piano is larger than the the distance covered by all of the other keys.

SIDEBAR to the SIDEBAR to the SIDEBAR: This also means that changing your sampling rate from 48 kHz to 96 kHz doubles your bandwidth, but only gives you an extra octave. However, this is not an argument against high-resolution audio, since the frequency range of the output is a small part of the list of pro’s and con’s.)

This is why people who deal with audio don’t use percent – ever. Instead, we use an extra bit of math that uses an evil concept called a logarithm to help to make things make more sense.

What is a logarithm?

If I say the following, you should not raise your eyebrows:

2*3 = 6, therefore 6/2 = 3 and 6/3 = 2

In other words, division is just multiplication done backwards. This can be generalised to the following:

if a*b=c, then c/a=b and c/b=a

Logarithms are similar; they’re just exponents done backwards. For example:

102 = 100, therefore Log10(100) = 2

and generally:

AB=C, therefore LogA(C) = B

Why use a logarithm?

The nice thing about logarithms is that they are a convenient way for a mathematician to do addition instead of multiplication.

For example, if I have the following sequence of numbers:

2, 4, 8, 16, 32, 64, and so on…

It’s easy to see that I’m just multiplying by 2 to get the next number.

What if I were to express the number sequence above as a series of exponents? Then it would look like this:

21, 22, 23, 24, 25, 26

Not useful yet…

What if I asked you to multiply two numbers in that sequence? Say, for example, 1024 * 8192. This would take some work (or at least some scrambling, looking for the calculator app on your phone…). However, it helps to know that this is the same as asking you to multiply 210 * 213 – to which the answer is 223. Notice that 23 is merely 10+13. So, I’ve used exponents to convert the problem from multiplication (1024*8192) to addition (210 * 213 = 2(10+13)).

How did I find out that 8192 = 213? By using a logarithm : Log2(8192) = 13.

In the old days, you would have been given a book of logarithmic tables in school, which was a way of looking up the logarithm of 8192. (Actually, those books were in base 10 and not base 2, so you would have found out that Log10(8192) = 3.9013, which would have made this discussion more confusing…) Nowadays, you can use an antique device called a “calculator” – a simulacrum of which is probably on a device you call a “phone” but is rarely used as such.

I will leave it to the reader to figure out why this quality of logarithms (that they convert multiplication into addition) is why slide rules work.

So what?

Let’s go back to the problem: We want to make a volume slider (or knob) where an equal distance (or rotation) corresponds to an equal change in level. Let’s do a simple one that has 10 steps. Coming down from “maximum” (which we’ll say is a gain of 1 or 100%), it could look like these:

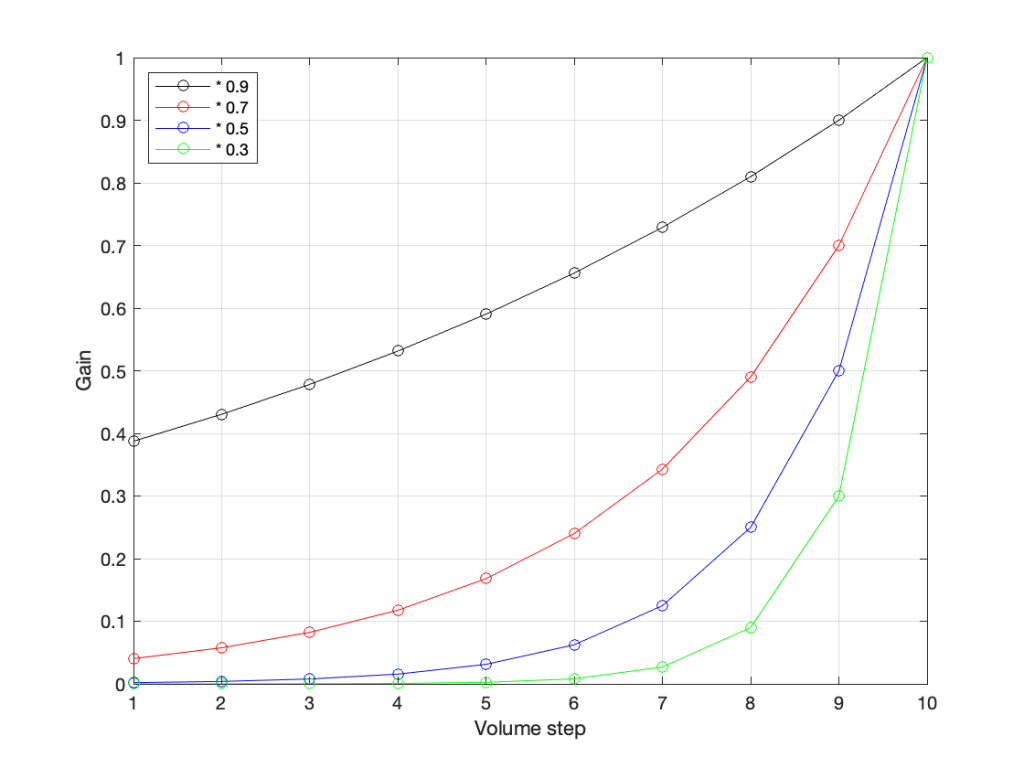
The gain values for four different versions of a 10-step volume control.

The plot above shows four different options for our volume controller. Starting at the maximum (volume step 10) and working downwards to the left, each one drops by the same perceived amount per step. The Black plot shows a drop of 90% per step, the red plot shows a drop of 70% per step (which matches the list of values I put above), Blue is 50% per step, and green is 30% per step.

As you can see, these lines are curved. As you can also see, as you get lower and lower, they get to the point where it gets harder to see the value (for example, the green curve looks like it has the same gain value for Volume steps 1 through 4).

However, we can view this a different way. If we change the scale of our graph’s Y-Axis to a logarithmic one instead of a linear one, the exact same information will look like this:

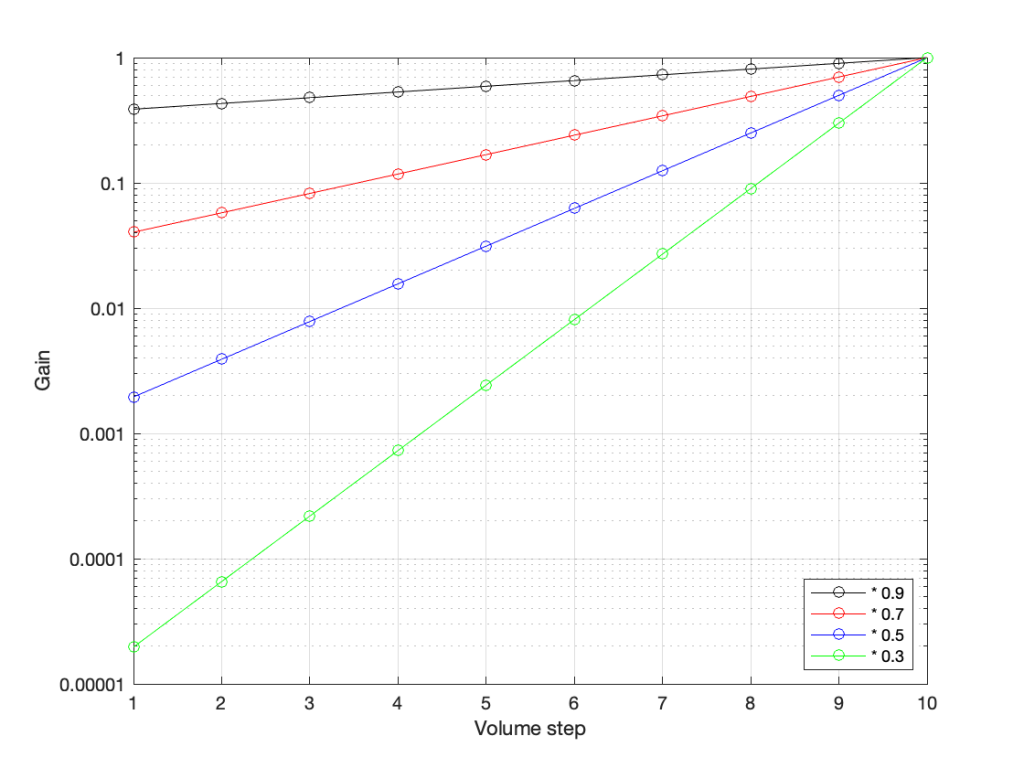
The same data plotted using a different scale for the Y-Axis.

Notice now that the Y-axis has an equal distance upwards every time the gain multiplies by 10 (the same way the music staff had the same distance every time we multiplied the frequency by 2). By doing this, we now see our gain curves as straight lines instead of curved ones. This makes it easy to read the values both when they’re really small and when they’re (comparatively) big (those first 4 steps on the green curve don’t look the same on that plot).

So, one way to view the values for our Volume controller is to calculate the gains, and then plot them on a logarithmic graph. The other way is to build the logarithm into the gain itself, which is what we do. Instead of reading out gain values in percent, we use Bels (named after Alexander Graham Bell). However, since a Bel is a big step, we we use tenths of a Bel or “decibels” instead. (… In the same way that I tell people that my house is 4,000 km, and not 4,000,000 m from my Mom’s house because a metre is too small a division for a big distance. I also buy 0.5 mm pencil leads – not 0.0005 m pencil leads. There are many times when the basic unit of measurement is not the right scale for the thing you’re talking about.)

In order to convert our gain value (say, of 0.7) to decibels, we do the following equation:

20 * Log10(gain) = Gain in dB

So, we would say

20 * Log10(0.7) = -3.01 dB

I won’t explain why we say 20 * the logarithm, since this is (only a little) complicated.

I will explain why it’s small-d and capital-B when you write “dB”. The small-d is the convention for “deci-“, so 1 decimetre is 1 dm. The capital-B is there because the Bel is named after Alexander Graham Bell. This is similar to the reason we capitalize Hz, V, A, and so on…

So, if you know the linear gain value, you can calculate the equivalent in decibels. If I do this for all of the values in the plots above, it will look like this:

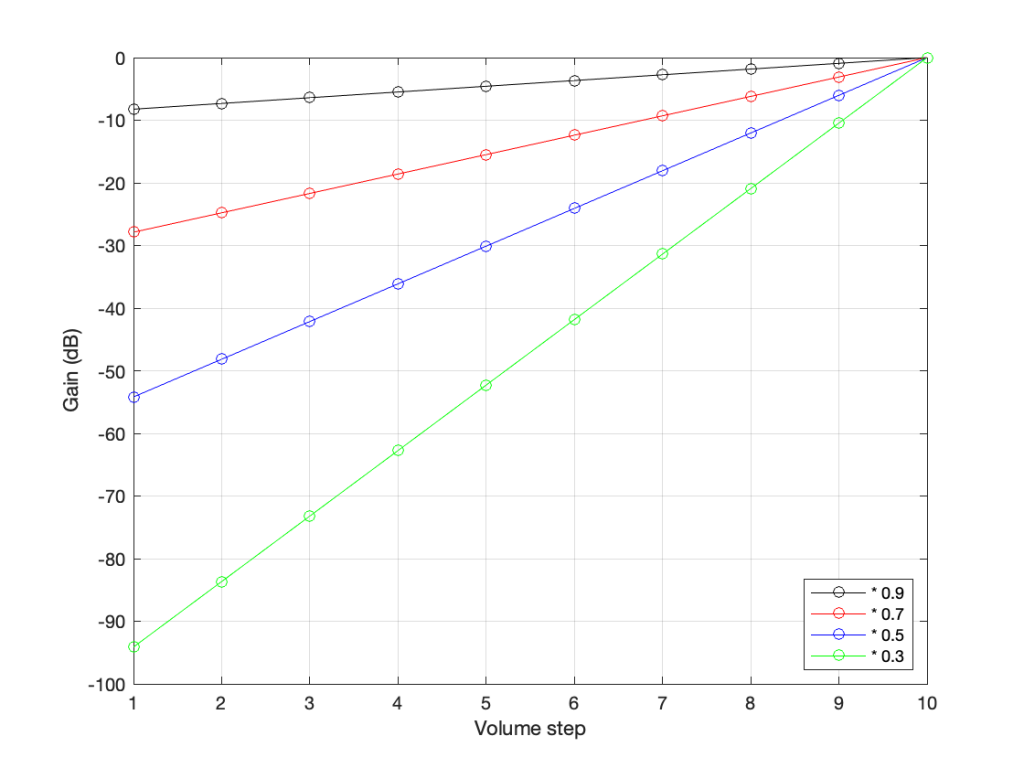
Notice that, on first glance, this looks exactly like the plot in the previous figure (with the logarithmic Y-Axis), however, the Y-Axis on this plot is linear (counting from -100 to 0 in equal distances per step) because the logarithmic scaling is already “built into” the values that we’re plotting.

For example, if we re-do the list of gains above (with a little rounding), it becomes

100% = 0 dB
70% = -3 dB
49% = -6 dB
34% = -9 dB
24% = -12 dB
17% = -15 dB
12% = -18 dB
8% = -21 dB

Notice coming down that list that each time we multiplied the linear gain by 0.7, we just subtracted 3 from the decibel value, because, as we see in the equation above, these mean the same thing.

This means that we can make a volume control – whether it’s a slider or a rotating knob – where the amount that you move or turn it corresponds to the change in level. In other words, if you move the slider by 1 cm or rotate the knob by 10º – NO MATTER WHERE YOU ARE WITHIN THE RANGE – the change is level will be the same as if you made the same movement somewhere else.

This is why Bang & Olufsen devices made since about 1990 (give or take) have a volume control in decibels. In older models, there were 79 steps (0 to 78) or 73 steps (0 to 72), which was expanded to 91 steps (0 to 90) around the year 2000, and expanded again recently to 101 steps (0 to 100). Each step on the volume control corresponds to a 1 dB change in the gain. So, if you change the volume from step 30 to step 40, the change in level will appear to be the same as changing from step 50 to step 60.

Volume Step ≠ Output Level

Up to now, all I’ve said can be condensed into two bullet points:

  • Volume control is a change in the gain value that is multiplied by the incoming signal
  • We express that gain value in decibels to better match the way we hear changes in level

Notice that I didn’t say anything in those two statements about how loud things actually are… This is because the volume setting has almost nothing to do with the level of the output, which, admittedly, is a very strange thing to say…

For example, get a DVD or Blu-ray player, connect it to a television, set the volume of the TV to something and don’t touch it for the rest of this experiment. Now, put in a DVD copy of any movie that has ONLY dialogue, and listen to how loud it sounds. Then, take out the DVD and put in a CD of Metallica’s Death Magnetic, press play. This will be much, much louder. In fact, if you own a B&O TV, the difference in level between those two things is the same as turning up the volume by 31 steps, which corresponds to 31 dB. Why?

When re-recording engineers mix a movie, they aim to make the dialogue sit around a level of 31 dB below maximum (better known as -31 dB FS or “31 decibels below Full Scale”). This gives them enough “headroom” to get much louder for explosions and gunshots to be exciting.

When a mixing engineer and a mastering engineer work on a pop or rock album, it’s not uncommon for them to make it as loud as possible, aiming for maximum (better known as 0 dB FS).

This means that a movie’s dialogue is much quieter than Metallica or Billie Eilish or whomever is popular when you’re reading this, because Metallica is as loud as the explosions in the movie.

The volume setting is just a value that changes that input level… So, If I listen to music at volume step 42 on a Beovision television, and you watch a movie at volume step 73 on the same Beovision television, it’s possible that we’re both hearing the same sound pressure level in our living rooms, because the music is 31 dB louder than the movie, which is the same amount that I’ve turned down my TV relative to yours (73-42 = 31).

In other words, the Volume Setting is not a predictor of how loud it is. A Volume Setting is a little like the accelerator pedal in your car. You can use the pedal to go faster or slower, but there’s no way of knowing how fast you’re driving if you only know how hard you’re pushing on the pedal.

What about other brands and devices?

This is where things get really random:

  • take any device (or computer or audio software)
  • play a sine wave (because thats easy to measure)
  • measure the change in output level as you change the volume setting
  • graph the result
  • Repeat everything above for different devices

You’ll see something like this:

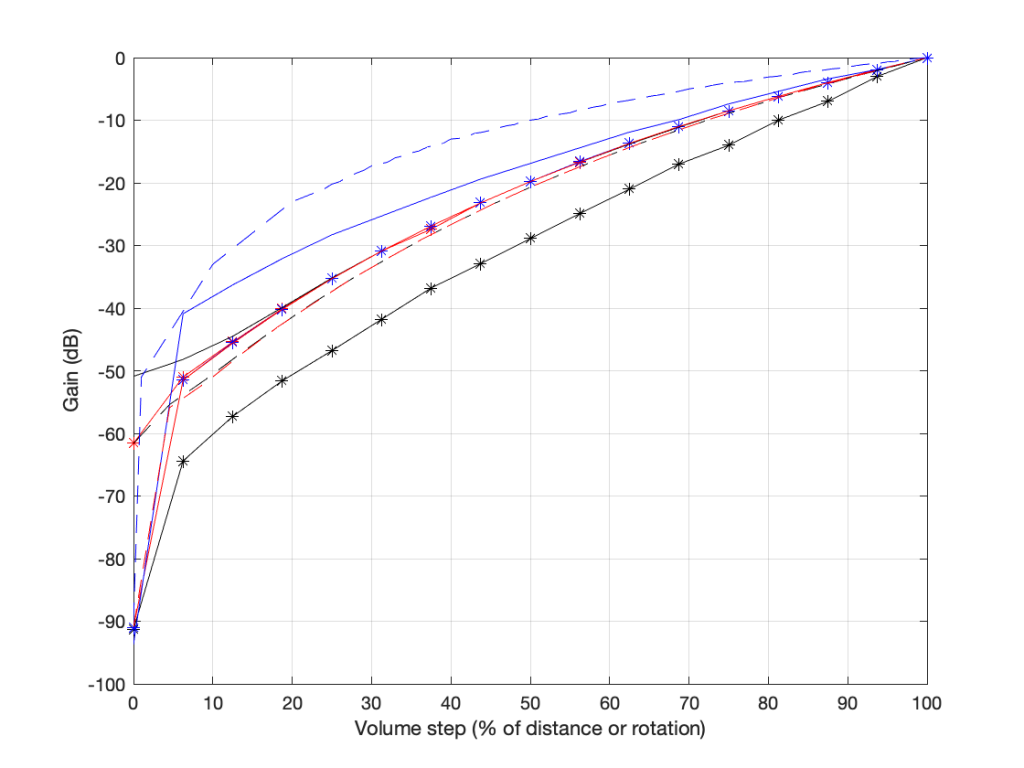
The gain vs. Volume step behaviours of 8 different devices / software players

there are two important things to note in the above plot.

  1. These are the measurements of 8 different devices (or software players or “apps”) and you get 8 different results (although some of them overlap, but this is because those are just different version numbers of the same apps).
    • Notice as well that there’s a big difference here. At a volume setting of “50%” there’s a 20 dB difference between the blue dashed line and the black one with the asterisk markings. 20 dB is a LOT.
  2. None of them look like the straight lines seen in the previous plot, despite the fact that the Y-axis is in decibels. In ALL of these cases, the biggest jumps in level happen at the beginning of the volume control (some are worse than others). This is not only because they’re coming up from a MUTE state – but because they’re designed that way to fool you. How?

Think about using any of these controllers: you turn it 25% of the way up, and it’s already THIS loud! Cool! This speaker has LOTS of power! I’m only at 25%! I’ll definitely buy it! But the truth is, when the slider / knob is at 25% of the way up, you’re already pushing close to the maximum it can deliver.

These are all the equivalent of a car that has high acceleration when starting from 0 km/h, but if you’re doing 100 km/h on the highway, and you push on the accelerator, nothing happens.

First impressions are important…

On the other hand (in support of thee engineers who designed these curves), all of these devices are “one-offs” (meaning that they’re all stand-alone devices) made by companies who make (or expect to be connected to) small loudspeakers. This is part of the reason why the curves look the way they do.

If B&O used those style of gain curves for a Beovision television connected to a pair of Beolab 90s, you’d either

  • be listening at very loud levels, even at low volume settings;
  • or you wouldn’t be able to turn it up enough for music with high dynamic range.

Some quick conclusions

Hopefully, if you’ve read this far and you’re still awake:

  • you will never again use “percent” to describe your volume level
  • you will never again expect that the output level can be predicted by the volume setting
  • you will never expect two devices of two different brands to output the same level when set to the same volume setting
  • you understand why B&O devices have so many volume steps over such a large range.

Typical Errors in Digital Audio: Part 8 – The Weakest Link

As a setup for this posting, I have to start with some background information…

Back when I was doing my bachelor’s of music degree, I used to make some pocket money playing background music for things like wedding receptions. One of the good things about playing such a gig was that, for the most part, no one is listening to you… You’re just filling in as part of the background noise. So, as the evening went on, and I grew more and more tired, I would change to simpler and simpler arrangements of the tunes. Leaving some notes out meant I didn’t have to think as quickly, and, since no one was really listening, I could get away with it.

If you watch the short video above, you’ll hear the same composition played 3 times (the 4th is just a copy of the first, for comparison). The first arrangement contains a total of 71 notes, as shown below.

Fig 1. Arrangement #1 – a total of 71 notes.

The second arrangement uses only 38 notes, as you can see in Figure 2, below.

Fig 2. Arrangement #2 – a total of 38 notes. A reduction in “data” of 46%.

The third arrangement uses even fewer notes – a total of only 27 notes, shown in Figure 3, below.

Fig 3. Arrangement #3 – a total of 27 notes. A reduction in “data” of 62% compared to the original.

 

The point of this story is that, in all three arrangements, the piece of music is easily recognisable. And, if it’s late in the night and you’ve had too much to drink at the wedding reception, I’d probably get away with not playing the full arrangement without you even noticing the difference…

A psychoacoustic CODEC (Compression DECompression) algorithm works in a very similar way. I’ll explain…

If you do an “audiometry test”, you’ll be put in a very, very quiet room and given a pair of headphones and a button. in an adjacent room is a person who sees a light when you press the button and controls a tone generator. You’ll be told that you’ll hear a tone in one ear from the headphones, and when you do, you should push the button. When you do this, the tone will get quieter, and you’ll push the button again. This will happen over and over until you can’t hear the tone. This is repeated in your two ears at different frequencies (and, of course, the whole thing is randomised so that you can’t predict a response…)

If you do this test, and if you have textbook-quality hearing, then you’ll find out that your threshold of hearing is different at different frequencies. In fact, a plot of the quietest tones you can hear at different frequencies it will look something like that shown in Figure 4.

 

Fig 4. A hand-drawn representation of a typical threshold of hearing curve.

 

This red curve shows a typical curve for a threshold of hearing. Any frequency that was played at a level that would be below this red curve would not be audible. Note that the threshold is very different at different frequencies.

Fig 5. A 1 kHz tone played at 70 dB SPL will obviously be audible, since it’s above the red line.

Interestingly, if you do play this tone shown in Figure 5, then your threshold of hearing will change, as is shown in Figure 6.

Fig 6. The threshold of hearing changes when an audible tone is played.

IF you were not playing that loud 1 kHz tone, and, instead, you played a quieter tone just below 2 kHz, it would also be audible, since it’s also above the threshold of hearing (shown in Figure 7.

Fig 7. A quieter tone at a higher frequency is also audible.

However, if you play those two tones simultaneously, what happens?

Fig 8. The higher frequency quieter tone is not audible in the presence of the louder, lower-frequency tone.

 

This effect is called “psychoacoustic masking” – the quieter tone is masked by the louder tone if the two area reasonably close together in frequency. This is essentially the same reason that you can’t hear someone whispering to you at an AC/DC concert… Normal people call it being “drowned out” by the guitar solo. Scientists will call it “psychoacoustic masking”.

 

Let’s pull these two stories together… The reason I started leaving notes out when I was playing background music was that my processing power was getting limited (because I was getting tired) and the people listening weren’t able to tell the difference. This is how I got away with it. Of course, if you were listening, you would have noticed – but that’s just a chance I had to take.

If you want to record, store, or transmit an audio signal and you don’t have enough processing power, storage area, or bandwidth, you need to leave stuff out. There are lots of strategies for doing this – but one of them is to get a computer to analyse the frequency content of the signal and try to predict what components of the signal will be psychoacoustically masked and leave those components out. So, essentially, just like I was trying to predict which notes you wouldn’t miss, a computer is trying to predict what you won’t be able to hear…

This process is a general description of what is done in all the psychoacoustic CODECs like MP3, Ogg Vorbis, AC-3, AAC, SBC, and so on and so on. These are all called “lossy” CODECs because some components of the audio signal are lost in the encoding process. Of course, these CODECs have different perceived qualities because they all have different prediction algorithms, and some are better at predicting what you can’t hear than others. Also, depending on what bitrate is available, the algorithms may be more or less aggressive in making their decisions about your abilities.

 

There’s just one small problem… If you remove some components of the audio signal, then you create an error, and the creation of that error generates noise. However, the algorithm has an trick up its sleeve. It knows the error it has created, it knows the frequency content of the signal that it’s keeping (and therefore it knows the resulting elevated masking threshold). So it uses that “knowledge” to  shape the frequency spectrum of the error to sit under the resulting threshold of hearing, as shown by the gray area in Figure 9.

Fig 9. The black vertical line is the content that is kept by the encoder. The red line is the resulting elevated threshold of hearing. The gray area is the noise-shaped error caused by the omission of some frequency components in the original signal.

 

Let’s assume that this system works. (In fact, some of the algorithms work very well, if you consider how much data is being eliminated… There’s no need to be snobbish…)

 

Now to the real part of the story…

Okay – everything above was just the “setup” for this posting.

For this test, I put two .wav files on a NAS drive. Both files had a sampling rate of 48 kHz, one file was a 16-bit file and the other was a 24-bit file.

On the NAS drive, I have two different applications that act as audio servers. These two applications come from two different companies, and each one has an associated “player” app that I’ve put on my phone. However, the app on the phone is really just acting as a remote control in this case.

The two audio server applications on the NAS drive are able to stream via my 2.4 GHz WiFi to an audio device acting as a receiver. I captured the output from that receiver playing the two files using the two server applications. (therefore there were 4 tests run)

Fig 10. A block diagram of the system under test.

The content of the signal in the two .wav files was a swept sine tone, going from 20 Hz to 90% of Nyquist, at 0 dB FS. I captured the output of the audio device in Figure 10 and ran a spectrogram of the result, analysing the signal down to 100 dB below the signal’s level. The results are shown below.

Fig 11. A spectrogram of the output signal from the audio device using “Audio Server SW 1” playing the 48 kHz, 16-bit WAV file. This is good, since it shows only the signal, and no extraneous artefacts within 100 dB.

 

Fig 12. A spectrogram of the output signal from the audio device using “Audio Server SW 1” playing the 48 kHz, 24-bit WAV file. This is also good, since it shows only the signal, and no extraneous artefacts within 100 dB.

 

Fig 13. A spectrogram of the output signal from the audio device using “Audio Server SW 2” playing the 48 kHz, 16-bit WAV file. This is also good, since it shows only the signal, and no extraneous artefacts within 100 dB.

Fig 14. A spectrogram of the output signal from the audio device using “Audio Server SW 2” playing the 48 kHz, 24-bit WAV file. This is obviously not good…

So, Figures 11 and 13 show the same file (the 16-bit version) played to the same output device over the same network, using two different audio server applications on my NAS drive.

Figures 12 and 14 also show the same file (the 24-bit version). As is immediately obvious, the “Audio Server SW 2” is not nearly as happy about playing the 24-bit file. There is harmonic distortion (the diagonal lines parallel with the signal), probably caused by clipping. This also generates aliasing, as we saw in a previous posting.

However, there is also a lot of visible noise around the signal – the “fuzzy blobs” that surround the signal. This has the same appearance as what you would see from the output of a psychoacoustic CODEC – it’s the noise that the encoder tries to “fit under” the signal, as shown in Figure 9… One give-away that this is probably the case is that the vertical width (the frequency spread) of that noise appears to be much wider when the signal is a low-frequency. This is because this plot has a logarithmic frequency scale, but a CODEC encoder “thinks” on a linear frequency scale. So, frequency bands of equal widths on a linear scale will appear to be wider in the low end on a log scale. (Another way to think of this is that there are as many “Hertz’s” from 0 Hz to 10 kHz as there are from 10 kHz to 20 kHz. The width of both of these bands is 10000 Hz. However, those of us who are still young enough to hear up there will only hear the second of these as the top octave – and there are lots of octaves in the first one. (I know, if we go all the way to 0 Hz, then there are an infinite number of octaves, but I don’t want to discuss Zeno today…))

 

Conclusion

So, it appears that “Audio Server SW 2” on my NAS drive doesn’t like sending 24 bits directly to my audio device. Instead, it probably decodes the wav file, and transcodes the lossless LPCM format into a lossy CODEC (clipping the signal in the process) and sends that instead. So, by playing a “high resolution” audio file using that application, I get poorer quality at the output.

As always, I’m not going to discuss whether this effect is audible or not. That’s irrelevant, since it’s dependent on too many other factors.

And, as always, I’m not going to put brand or model names on any of the software or hardware tested here. If, for no other reason, this is because this problem may have already been corrected in a firmware update that has come out since I tested it.

The take-home messages here are:

  • an entire audio signal path can be brought down by one piece of software in the audio chain
  • you can’t test a system with one audio file and assume that it will work for all other sampling rates, bit depths and formats
    • Normally, when I run this test, I do it for all combinations of 6 sampling rates, 2 bit depths, and 2 formats (WAV and FLAC), at at least 2 different signal levels – meaning 48 tests per DUT
    • What I often see is that a system that is “bit perfect” in one format / sampling rate / bit depth is not necessarily behaving in another, as I showed above..

So, if you read a test involving a particular NAS drive, or a particular Audio Server application, or a particular audio device using a file format with a sampling rate and a bit depth and the reviewer says “This system worked perfectly.” You cannot assume that your system will also work perfectly unless all aspects of your system are identical to the tested system. Changing one link in the chain (even upgrading the software version) can wreck everything…

This makes life confusing, unfortunately. However, it does mean that, if someone sounds wrong to you with your own system, there’s no need to chase down excruciating minutiae like how many nanoseconds of jitter you have at your DAC’s input, or whether the cat sleeping on your amplifier is absorbing enough cosmic rays. It could be because your high-res file is getting clipped, aliased, and converted to MP3 before sending to your speakers…

Addendum

Just in case you’re wondering, I tested these two systems above with all 6 standard sampling rates (44.1, 48, 88.2, 96, 176.4, and 192 kHz), 2 bit depths (16 & 24). I also did two formats (WAV and FLAC) and three signal levels (0, -1, and -60 dB FS) – although that doesn’t matter for this last comment.

“Audio Server SW 2” had the same behaviour in the case of all sampling rates – 16 bit files played without artefacts within 100 dB of the 0 dB FS signal, whereas 24-bit files in all sampling rates exhibited the same errors as are shown in Figure 14.