Category: loudspeakers

Mixing closed and ported cabinets: Part 6

As I showed in Part 5, the phase response of a loudspeaker driver in a closed cabinet is different from one in a ported cabinet in the low frequency region because, the low frequency output of the ported system is actually coming from the port, not the driver.

If we take the phase response plots from the two systems shown in Part 5 and put them on the same graph, the result is Figure 1.

Figure 1

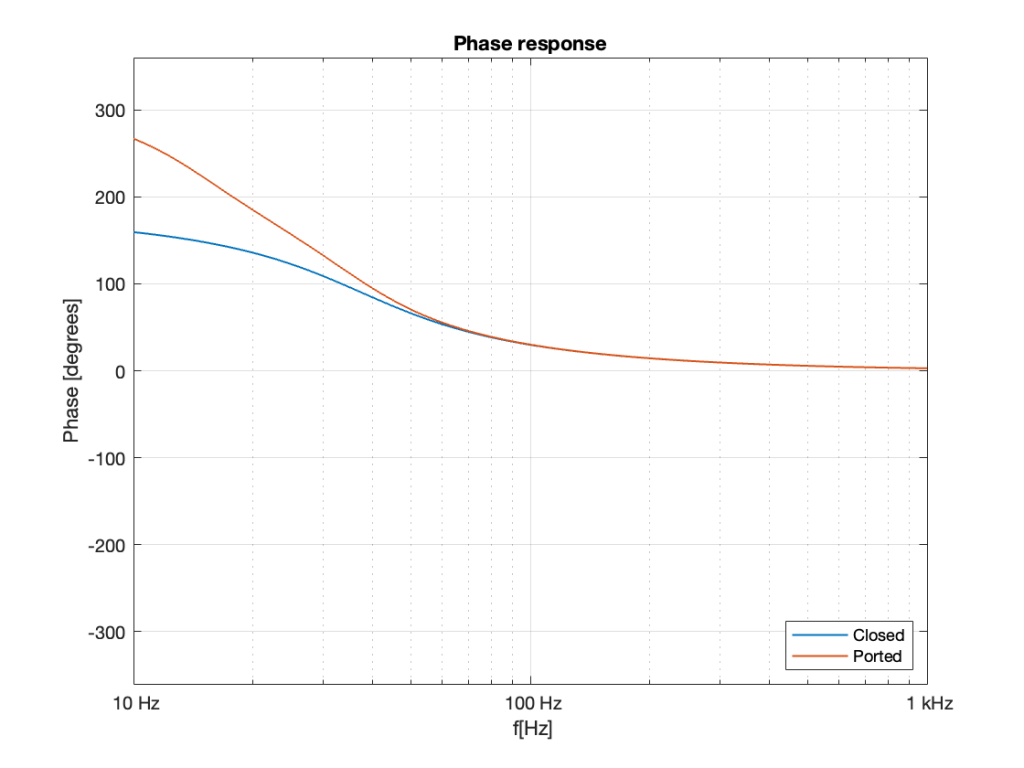
If we calculate the difference in these two plots by subtracting the blue curve from the red curve at each frequency then we can see that a ported cabinet is increasingly out of phase relative to a sealed cabinet as you go lower and lower in frequency. This difference is shown in Figure 2.

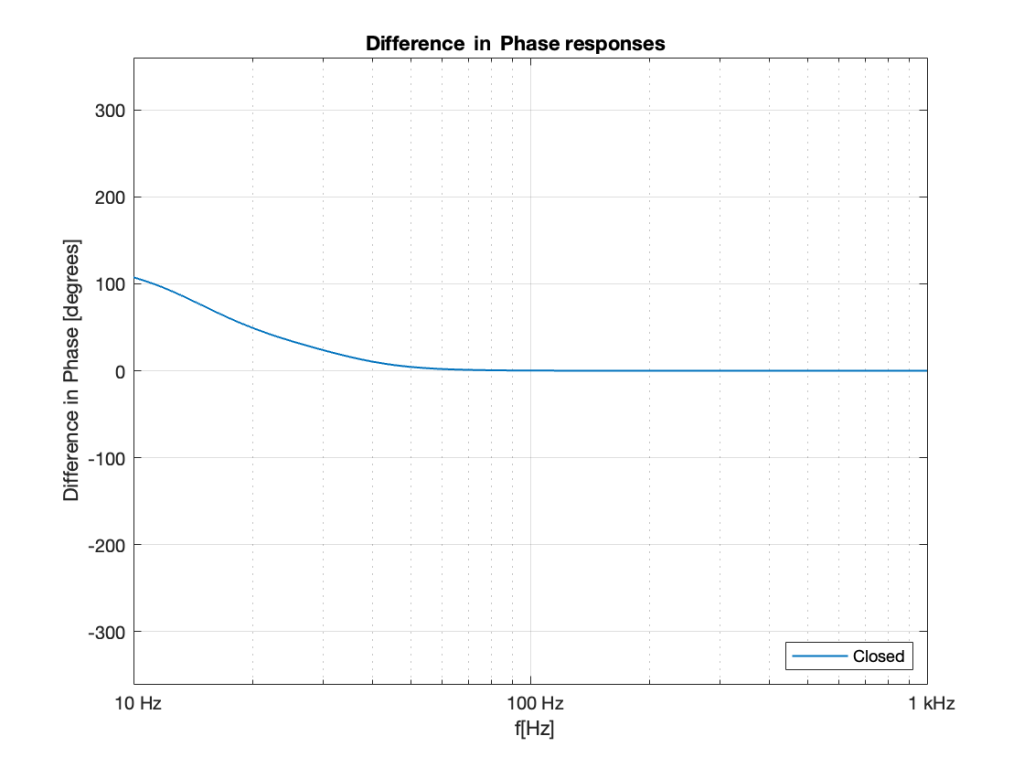
Now, don’t look at that graph and say “but you never get to 180º so what’s the problem?” All of the plots I’ve shown in this series are for one specific driver in one specific enclosure, with and without a port of one specific diameter and length. I could have been more careful and designed two different enclosures (with and without a port) that does get to 180º (or something else up to 180º).

In other words: “results may vary”. Every loudspeaker in every cabinet has some magnitude response and some phase response (these are directly related to each other), and they’ll all be different by different amounts. (This is also the reason why I’m neglecting to talk about the fact that, as you go lower in frequency, the ported loudspeaker also drops faster in output level, so even if it were a full 180º out of phase, it would cancel less and less when combined with the sealed cabinet loudspeaker.)

The point of all of this was to show that, if you take two different loudspeakers with two different enclosure types, you get two different phase responses, particularly in the low frequency region.

This means that if you take those two loudspeaker types (the original question that inspired this series was specifically about mixing Beolab 9, Beolab 20, and Beolab 2 in a system where all of those loudspeakers are “helping” to produce the bass) and play identical signals from them in the same room, it’s not only possible, but highly likely that they will wind up cancelling each other. This results in LESS bass instead of MORE, ignoring all other effects like loudspeaker placement, room modes, and so on.

But Beolab 2 has slave drivers, not ports…

Figure 3

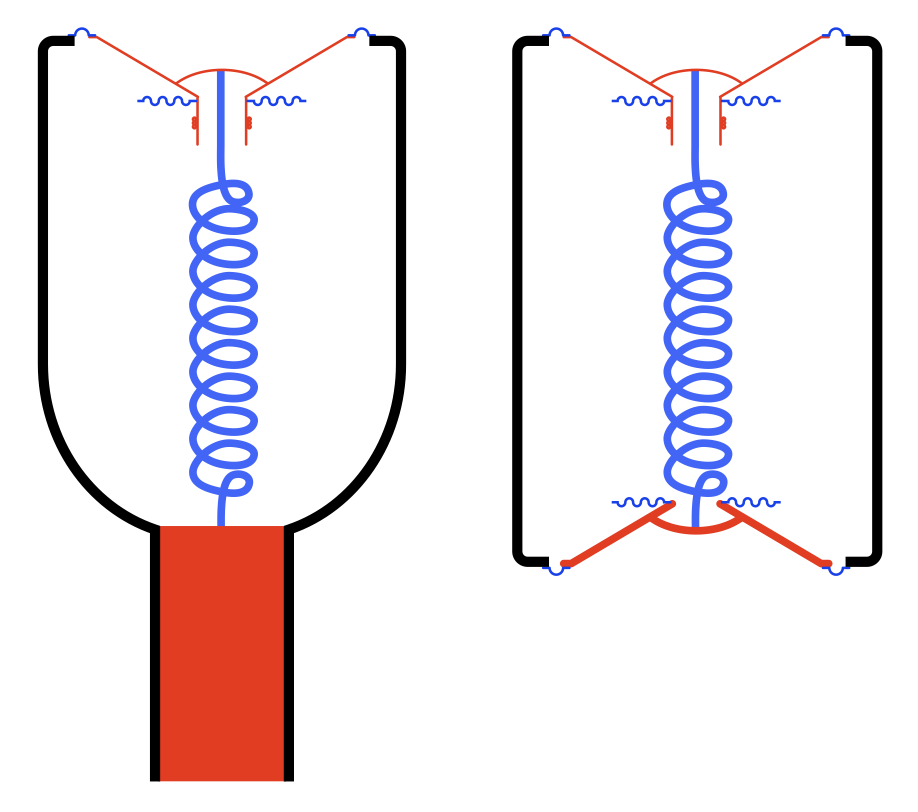
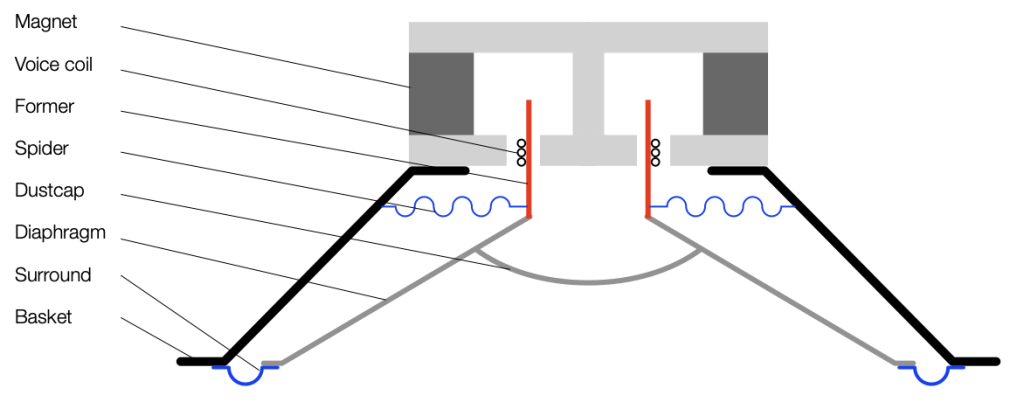
Take a look at Figure 3. I’ve shown a conceptual drawing of a ported loudspeaker (showing the mass of the air in the port as a red rectangle) on the left and a loudspeaker with a slave driver (on the bottom – notice it’s missing a former and voice coil, and the diaphragm is thicker to make it heavy) on the right.

This should make it intuitively obvious that a ported loudspeaker and an enclosure with a slave driver are effectively identical. This raises the question of why you would do one rather than the other.

The advantages of using a port instead of a slave driver is that a port will be more “stable” on a production line (since all of the ports on all the loudspeakers you make will be identical in size) and they’ve very cheap to make. The disadvantage of a port is that if the velocity of the air moving in and out of it is too high, then you hear it “chuffing”, which is a noise caused by turbulence around the edges of the port. (If you blow across the top of a wine bottle, you don’t hear a perfect sine wave, you hear a very noisy “breathy” one. The noise is the chuffing.)

The advantage of a slave driver is that you don’t get any turbulence, and therefore no chuffing. A slave driver can also be heavier than the air in a port in a smaller space, so you can get the response of a large port in a smaller loudspeaker. There is a small disadvantage in the fact that there will be production line tolerance variations (but this is not really a big worry), and then there’s the price, which is much higher than a hole in a box.

This means that if you take anything I’ve said above about ported loudspeakers, and replace the word “port” with “slave driver” then it’s still true.

P.S.

If you do have a surround system that not only has a bass management system, but is also capable of re-directing the bass to more loudspeakers than just your subwoofer (as is the case with all current Bang & Olfusen surround processors in the televisions), then all of this is important to remember. You can’t just send the bass to more loudspeakers and expect to get more output. You might get less.

This is true unless you have a Beosound Theatre. This is because the Theatre has an extra bit of processing in the signal path called “Phase Compensation” which applies an allpass filter to the outputs, compensating for the phase differences between loudspeakers in the low frequency region. So, in this one particular case, you should expect to get more output from more loudspeakers.

Mixing closed and ported cabinets: Part 5

Let’s build a ported box and put a woofer in it. If we measure the magnitude responses of the individual outputs of the driver and the port as well as the total output of the entire loudspeaker, they might look like the three curves shown in Figure 1.

Figure 1

If you take a look at the curves at 1 kHz, you can see that the total output (the blue curve) is the same as the woofer’s output (the red curve) because the port’s output (the yellow curve) is so low that it’s not contributing anything.

As we come down in frequency, we see the output of the port coming up and the output of the driver coming down. At around 20 Hz, the port reaches its maximum output and the woofer reaches its minimum as a result. In fact that woofer’s output is about 15 dB lower than the port’s at that frequency.

As we go farther down in frequency, we can see that the woofer comes up and then starts to drop again, but the port just drops in level the lower we go.

Now look at the total output (the blue curve) from 20 Hz and down. Notice that the total output of the system from 20 Hz down to about 15 Hz is LOWER than the output of the port alone. As you go below about 15 Hz, you can see that the total output is lower than either the woofer or the port.

This means that the port and the woofer are cancelling each other, just like I described in the previous part in this series. This can be seen when we look at their respective phase responses, shown in the middle plot in Figure 2. I’ve also plotted the difference in the woofer and the port phase responses in the bottom plot.

Figure 2

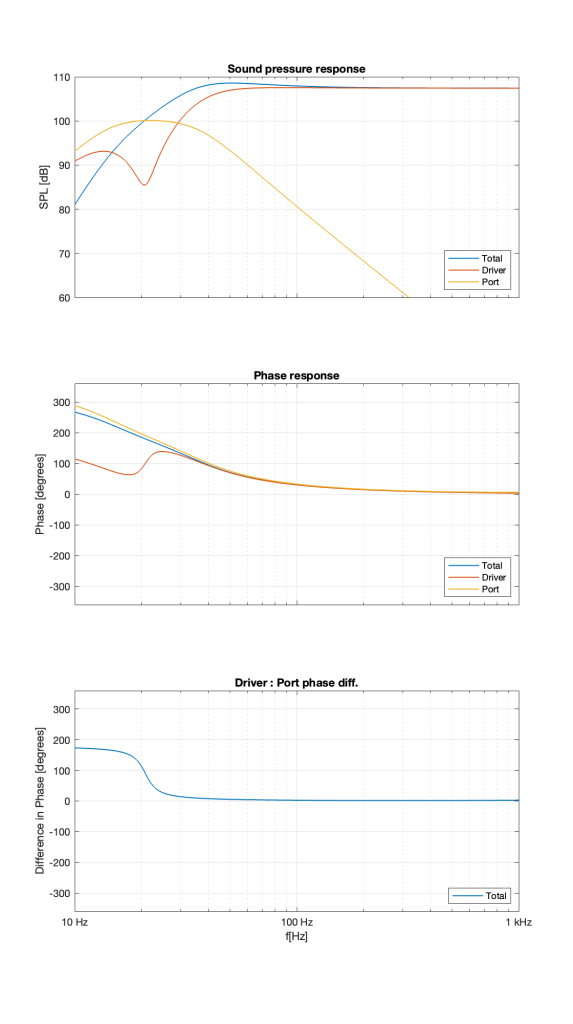
Notice that, below 20 Hz, the woofer and the port are about 180º apart. So, as the woofer moves out of the enclosure, the air in the port moves inwards, and the total sum is less than either of the two individual outputs.

What happens when you put a woofer in a sealed enclosure instead of one with a port? The responses from this kind of system are shown below in Figure 3.

Figure 3

The first thing that you’ll notice in the plots in Figure 3 is that there is only one curve in each graph. This is because the total output is the driver output.

You’ll also notice in the top plot that a woofer in a cabinet acts as a second-order high-pass filter because the cabinet is not too small for the driver. If the cabinet were smaller, then you’d see a peak in the response, but let’s say that I’m not that dumb…

Because it’s a second-order high-pass filter, it has a phase response that approaches 180º as you go down in frequency.

Now, compare that phase response in the low end of Figure 3 to the phase response of the low end in Figure 2. This is where we’re headed, since the purpose of all of this discussion is to talk about what happens when you have a system that combines sealed enclosures with ported ones. That brings us to Part 6.

Mixing closed and ported cabinets: Part 4

In Part 1, I showed how a wine bottle behaves exactly like a mass on a spring where the mass is the cylinder of air in the bottle’s neck and the spring is the air inside the bottle itself.

Figure 1

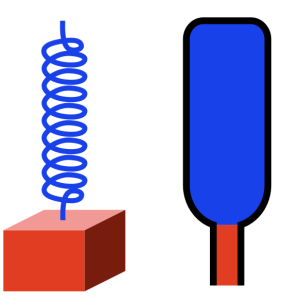
I also showed how a loudspeaker driver (like a woofer) in a closed box is the same thing, where the spring is the combination of the surround, the spider and the air in the box.

Figure 2

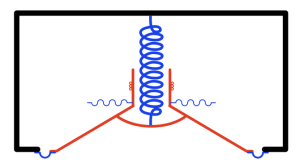
But what happens if the speaker enclosure is not sealed, but instead is open to the outside world through a “port” which is another way of saying “a tube”. Then, conceptually, you are combining the loudspeaker driver with the wine bottle like I’ve shown in Figure 3.

Figure 3

If I were to show this with all the masses in red and all the springs in blue, it would look like Figure 4.

Figure 4

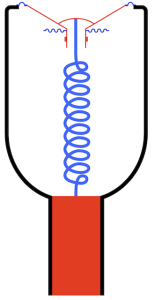
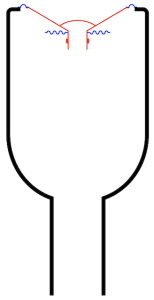
Now things are getting a little complicated, so let’s take things slowly… literally.

If the loudspeaker driver in Figure 4 moves into the cabinet very slowly (say, you push it with your fingers or you play a very low frequency with an electrical signal), then the air that it displaces in of the bottle (the enclosure) will just push the plug of air out the bottle’s neck (the port). The opposite will happen if you pull the driver out of the enclosure: you’ll suck air into the port.

If, instead you move the driver back and forth very quickly (by playing a very high frequency) then the inertia of the air inside the cabinet (shown as the big blue spring in the middle) prevents it from moving down near the port. In fact, if the frequency is high enough, then the air at the entrance of the port doesn’t move at all. This means that, for very high frequencies, the system will behave exactly the same as if the enclosure were sealed.

But somewhere between the very low frequencies and the very high frequencies, there is a “magic” frequency where the air in the port resonates, and there, things don’t behave intuitively. At that frequency, whenever the driver is trying to move into the enclosure, the air in the port is also moving into the enclosure. And, although the air has less mass than the driver, it’s free to move more. The end result is that, at the port’s resonant frequency, the driver (in theory) doesn’t move at all*, and the air in the port is moving a lot.**

In other words, you can think of a single driver in a ported cabinet as being basically the same as a two-way loudspeaker, where the woofer (for example) is one driver and the port is the other “driver”.

  • At high frequencies, the sound is only coming out of the woofer (for example).
  • As you come down in frequency and get closer to the port’s resonance, you get less and less from the woofer and more and more from the port.
  • At the port’s resonant frequency, all* of the sound is coming from the movement of the air in and out of the port
  • As you go lower than the port’s resonant frequency, the woofer starts working again, but now as the woofer moves out of the enclosure (making a positive pressure) it sucks air into the port (making a negative pressure). So, at very low frequencies, the woofer is working very hard, but you get very little sound output because the port cancels it out.

If you look at this as a magnitude response (the correct term for “frequency response” for this discussion), you can think of the woofer having one response, the port having a different response, and the two adding together somehow to produce a total response for the entire loudspeaker.

However, as you can see from the short 4-point list above, something happens with the phase of the signal at different frequencies. This is most obvious in the “very low frequency” part, where the woofer’s and the port’s outputs are 180º out of phase with each other.

In Part 5 we’ll look at these different components of the total output separately, both in terms of magnitude and phase responses (which, combined are the frequency response).

* Okay okay…. I say “the driver (in theory) doesn’t move at all” and “all of the sound is coming from the movement of the air in and out of the port” which is a bit of an exaggeration. But it’s not MUCH of an exaggeration…

** This is an oversimplified explanation. The slightly less simplified version is that the air inside the cabinet is acting like a spring that’s getting squeezed from two sides: the driver and the air in the port. The driver “sees” the “spring” (the air in the box) as pushing and pulling on it just as much as its pulling and pushing, so it can’t move (very much…).

Mixing closed and ported cabinets: Part 3

Before starting on this portion of the series, I’ll ask you to think about how little energy (or movement) it takes to get a resonant system oscillating. For example, if you have a child on a swing, a series of very gentle pushes at the right times can result in them swinging very high. Also, once the child is swinging back and forth, it takes a lot of effort to stop them quickly.

Moving onwards…

So far, we’ve seen that a loudspeaker driver in a closed cabinet can be thought of as just a mass on a spring, and, as a result, it has some natural resonance where it will oscillate at some frequency.

The driver is normally moved by sending an electrical signal into its voice coil. This causes the coil to produce a magnetic field and, since it’s already sitting in the magnetic field of a permanent magnet, it moves. The surround and spider prevent it from moving sideways, so it can only move outwards (if we send electrical current in one direction) or inwards (if we send current in the other direction).

When you try to move the driver, you’re working against a number of things:

  • the inertia of the mass of the moving parts
    Pick up a heavy book, for example, and try to push and pull it back and forth. It’s hard work!
  • the inertia of the air directly in front of and behind the driver
    Pick up a big sheet of stiff plastic (like the thing you put on the floor under an office chair) and try to push it back and forth. It’s also hard work!
  • the compliance (springiness) of the surround, spider, and air trapped in the cabinet behind the driver
    Blow up a ballon, and use your two hands to squeeze it repeatedly. It’s also hard work!

These three things can be considered separately from each other as a static effect. In other words:

  • It’s hard work to pick up a book or push a car that’s broken down (forget about pushing-and-pulling – just push OR pull)
  • It’s hard work to run into a headwind with that big piece of stiff plastic
  • It’s hard work to squeeze a balloon and keep it compressed

But, if you’re pushing AND pulling the loudspeaker driver there is another effect that’s dynamic.

When you’re moving the driver at a VERY low frequency, you’re mostly working against the “spring” which is probably quite easy to do. So, at a low frequency, the driver is pretty easy to move, and it’s moving so slowly that it doesn’t push back electrically. So, it does not impede the flow of current through the voice coil.

When you’re moving the driver at a VERY high frequency, you’re mostly working against the inertia of the moving parts and the adjacent air molecules. The higher the frequency, the harder it is to move the driver.

However, when you’re trying to moving the driver at exactly the resonant frequency of the driver, you don’t need much energy at all because it “wants” to move at that same rate. However, at that frequency, the voice coil is moving in the magnetic field of the permanent magnet, and it generates electricity that is trying to move current in the opposite direction of what your amp is going. In other words, at the driver’s resonant frequency, when you’re trying to push current into the voice coil, it generates a current that pushes back. When you try to pull current out of the voice coil, it generates a current that pulls back.

In other words, at the driver’s resonant frequency, your amplifier “sees” the driver as as a thing that is trying to impede the flow of electrical current. This means that you get a lot of movement with only a little electrical current; just like the child on the swing gets to go high with only a little effort – but only at one frequency.

This is a nice, simple case where you have a moving mass (the moving parts of the driver) and a spring (the surround, spider, and air in the sealed box). But what happens when the speaker has a port?

On to Part 4…

Mixing closed and ported cabinets: Part 2

Let’s look at a typical moving coil loudspeaker driver like the woofer shown in Figure 1.

Figure 1.

If I were to draw a cross-section of this and display it upside-down, it would look like Figure 2.

Figure 2.

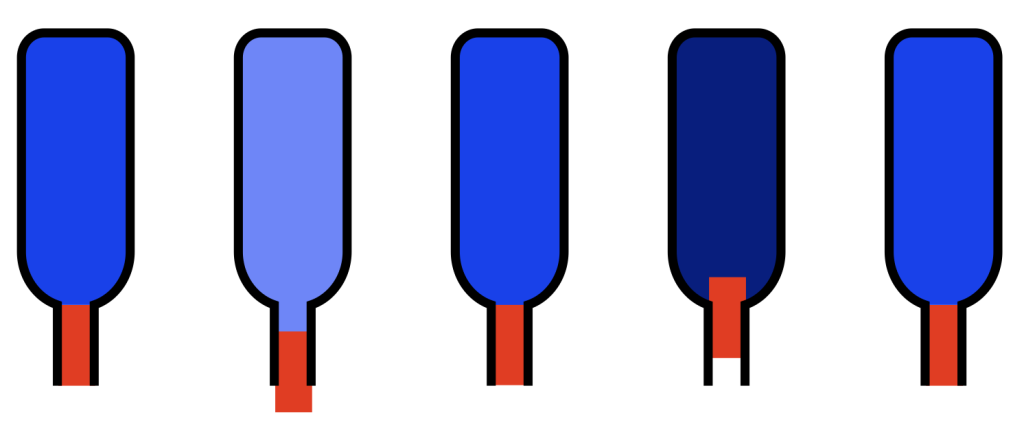
Typically, if we send a positive voltage/current signal to a driver (say, the attack of a kick drum to a woofer) then it moves “forwards” or “outwards” (from the cabinet, for example). It then returns to the rest position. If we send it a negative signal, then it moves “backwards” or “inwards”. This movement is shown in Figure 3.

Figure 3.

Notice in Figure 3 that I left out all of the parts that don’t move: the basket, the magnet and the pole piece. That’s because those aren’t important for this discussion.

Also notice that I used only two colours: red for the moving parts that don’t move relative to each other (because they’re all glued together) and blue for the stretchy parts that act as a spring. These colours relate directly to the colours I used in Part 1, because they’re doing exactly the same thing. In other words, if you hold a woofer by the basket or magnet, and tap it, it will “bounce” up and down because it’s just a mass suspended by a spring. And, just like I talked about in Part 1, this means that it will oscillate at some frequency that’s determined by the relationship of the mass to the spring’s compliance (a fancy word for “springiness” or “stiffness” of a spring. The more compliant it is, the less stiff.) In other words, I’m trying to make it obvious that Figure 3, above is exactly the same as Figures 3 and 5 in Part 1.

However, it’s very rare to see a loudspeaker where the driver is suspended without an enclosure. Yes, there are some companies that do this, but that’s outside the limits of this discussion. So, what happens when we put a loudspeaker driver in a sealed cabinet? For the purposes of this discussion, all it means is that we add an extra spring attached to the moving parts.

Figure 4

I’ve shown the “spring” that the air provides as a blue coil attached to the back of the dust cap. Of course, this is not true; the air is pushing against all surfaces inside the loudspeaker. However, from the outside, if you were actually pushing on the front of the driver with your fingers, you would not be able to tell the difference.

This means that the spring that pushes or pulls the loudspeaker diaphragm back into position is some combination of the surround (typically made of rubber nowadays), the spider (which might be made of different things…) and the air in the sealed cabinet. Those three springs are in parallel, so if you make one REALLY stiff (or lower its compliance) then it becomes the important spring, and the other two make less of a difference.

So, if you make the cabinet too small, then you have less air inside it, and it becomes the predominant spring, making the surround and spider irrelevant. The bigger the cabinet, the more significant a role the surround and spider play in the oscillation of the system.

Sidebar: If you are planning on making a lot of loudspeakers on a production line, then you can use this to your advantage. Since there is some variation in the compliance of the surround and spider from driver-to-driver, then your loudspeakers will behave differently. However, if you make the cabinet small, then it becomes the most important spring in the system, and you get loudspeakers that are more like each other because their volumes are all the same.

Remember from part 1 that if you increase the stiffness of the spring, then the resonant frequency of the oscillation will increase. It will also ring for longer in time. In practical terms, if you put a woofer in a big sealed cabinet and tap it, it will sound like a short “thump”. But if the cabinet is too small, then it will sound like a higher-pitched and longer-ringing “bonnnnnnnggggg”.

So far, we’ve only been talking about physical things: masses and springs. In the next part, we’ll connect the loudspeaker driver to an amplifier and try to push and pull it with electrical signals.

Mixing closed and ported cabinets: Part 1

I made a comment on a forum this week, commenting that, if you mix loudspeakers with closed cabinets with loudspeakers with ported cabinets (or slave drivers), the end result can be a reduction in total output: less sound from more loudspeakers. Of course, the question is “why?” and the short answer is “due to the phase mismatching of the loudspeakers”.

This is the long answer.

Before we begin, we have to get an intuitive understanding of what a ported loudspeaker is. (Note that I’ll keep saying “ported loudspeaker”, but the principle also applies to loudspeakers with slave drivers, as I’ll explain later.) Before we get to a ported loudspeaker, we need to talk about Helmholtz resonators.

Take a block that’s reasonably heavy and hang it using a spring so that it looks like this:

Figure 1.

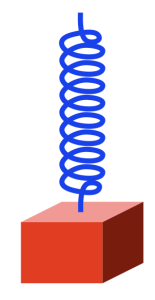
The spring is a little stretched because the weight of the block (which is the result of its mass and the Earth’s gravity) is pulling downwards. (We’ll ignore the fact that the spring is also holding up its own weight. Let’s keep this simple…) However, it doesn’t fall to the floor because the spring is pulling upwards.

Now pull downwards on the block, so it will look like the example on the right in the figure below.

Figure 2.

The spring is stretched because we’re pulling down on the block. The spring is also pulling upwards more, since it’s pulling against the weight of the block PLUS the force that you’re adding in a downwards direction.

Now you let go of the block. What happens?

The spring is pulling “too hard” on the block, so the block starts rising back to where it started (we’ll call that the “resting position”). However, when it gets there, it has inertia (a body in motion tends to stay in motion… until it hits something big…) so it doesn’t stop. As a result, it moves upwards, higher than the resting position. This squeezes the spring until it gets to some point, at which time the block stops, and then starts going back downwards. When it returns to the resting position, it still has inertia, so it passes that point and goes too far down again. I’ve shown this as a series of positions from left to right in the figure below.

Figure 3

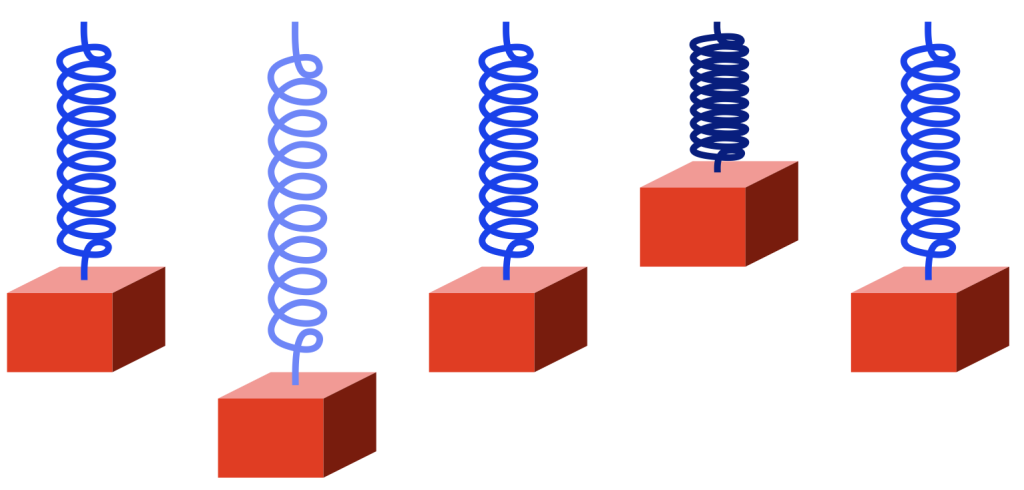
If there were no friction, no air around the block, and no friction within the metal molecules of the spring, then this would bounce up and down forever.

However, there is friction, so some of the movement (“kinetic energy”) is turned into heat and lost. So, each bounce gets smaller and smaller and the maximum velocity of the block (as it passes the resting position) gets lower and lower, until, eventually, it stops moving (at the resting position, where it started).

Notice that I changed the colour of the spring to show when it’s more stretched (lighter blue) and when it’s more compressed (darker blue).

If everything were behaving perfectly, then the RATE at which the bounce repeats wouldn’t change. Only its amplitude (or the excursion of the block, or the height of the bounce) would reduce over time. That bounce rate (let’s say 1 bounce per second, and by “bounce” I mean a full cycle of moment down, up, and back down to where it started again) is the frequency of the repetition (or oscillation).

If you make the weight lighter, then it will bounce faster (because the spring can pull the weight more “easily”). If you make the spring stiffer, then it will bounce faster (because the spring can pull the weight more “easily”). So, we can change the frequency of the oscillation by changing the weight of the block or the stiffness of the spring.

Now take a look at the same weight on a spring next to an up-side down wine bottle that (sadly) has been emptied of wine.

Figure 4.

Notice that I’ve added some colours to the air inside the bottle. The air in the bottle itself is blue, just like the colour of the spring. This is because, if we pull air out of the bottle (downwards), the air inside it will pull back (upwards; just like the metal spring pulling back upwards on the block). I’ve made the small cylinder of air in the neck of the bottle red, just like the block. This is because that air has some mass, and it’s free to move upwards (into the bottle) and downwards (out of the bottle) just like the block.

If I were somehow able to pull the “plug” of air out of the neck of the bottle, the air inside would try to pull it back in. If I then “let go”, the plug would move inwards, go too far (because it also has inertia), squeezing (or compressing) the air inside the bottle, which would then push the plug back out. This is shown in the figure below.

Figure 5.

At the level we’re dealing with, this behaviour is practically identical to the behaviour of the block on the spring. In other words, although the block and the plug are made of different materials, and although the metal spring and the air inside the bottle are different materials, Figures 3 and 5 show the same behaviour of the same kind of system.

How do you pull the plug of air out of the bottle? It’s probably easier to start by pushing it inwards instead, by blowing across the top.

When you do this, a little air leaks into the opening, pushing the plug inwards. The “spring” in the bottle then pushes the plug outwards, and your cycle has started. If you wanted to do the same thing with the block, you’d lift it and let go to start the oscillation.

However, you don’t need to blow across the bottle to make it oscillate. You can just tap it with the palm of your hand, for example. Or, if you put the bottle next to your ear and listen carefully, you’ll hear a note “singing along” with the sound in the room. This is because the air in the bottle resonates; it moves back and forth very easily at the frequency that’s determined by the mass of the air in the neck and the volume of air in of the bottle (the spring).

However, remember that friction can make the oscillation decay (or die away) faster, by turning the movement into heat.

One last thing…

There’s another way to get either the block or the wine bottle oscillating:

You can move the TOP of the spring (for example, if you pull it up, then the spring will pull the block upwards, and it’ll start bouncing). Or, you could tap the bottom of the wine bottle (which is on the top in my drawings).

This method of starting the oscillation will come in handy in part 2.

Internal vs. External Volume Control

#93 in a series of articles about the technology behind Bang & Olufsen

A question came to my desk this week from a customer who would like to connect a third-party streaming device to his Beolab 50s. He plans to use a USB-Audio connection and his question was “Should I control the volume of the audio signal in the streamer or in the Beolab 50s?” There are three different ways to configure these two options:

  1. Control the volume in the streamer using its interface, and send a signal that has been volume-regulated to the Beolab 50s, which should then be set to have a start up default volume such that the maximum volume on the streamer results in a level that is as loud as the customer will ever want it to be. In order to do this, the Beolab 50s need to be set to ignore the volume information that is received on the USB-Audio connection.
  2. Set the streamer to output an unregulated signal, and set the Beolab 50s to obey the volume information that is received on the USB-Audio connection, then use the streamer’s interface for the volume control (which would actually be happening inside the Beolab 50s).
  3. Set the streamer to output an unregulated signal, and set the Beolab 50s to disobey the volume information that is received on the USB-Audio connection, then use the Beolab 50’s interface for the volume control (which would actually be happening inside the Beolab 50s).

Of course, one way to answer the question is “where do you want to control the volume?” For example, if it’s with a remote control for the Beolab 50s, then the answer is “use option #3”. If you’d prefer to use the streamer’s app, for example, then the answer is “use option #1 or #2”.

However, the question came to my desk because it was specifically about the technical performance of the audio signal. Which of these three options results in the highest audio “quality”? (I put the word “quality” in quotation marks because it is a loaded term, and might mean different things to different persons…)

The simplest answer without getting into any details is “it probably doesn’t matter“. However, that answer is based on a couple of assumptions that may or may not be wrong.

Hypothetically, the Beolab 50 can output an audio signal that peaks at about 122 dB SPL measured at 1 m in a free field, albeit not at all frequencies present at its output. (This is because there are some physical limitations of how far the woofers can move, which means that you can’t get 122 dB SPL at 20 Hz, for example.) The noise floor of the Beolab 50s is about 0 dB SPL measured in the same place (again, this is frequency-dependent). So, it has a total dynamic range at its output of about 122 dB.

The maximum output level is a result of a combination of the loudspeaker drivers, the amplifiers, and the power supply, however, these have all been chosen to reach their maximum outputs approximately simultaneously, so changing one of the three won’t make a big difference.

The noise floor is a result of the combination of the loudspeaker drivers’ sensitivities, the amplifiers’ noise floors, and the signal that feeds the amplifiers: the DAC outputs’ noise floors. For the purposes of this discussion, I’m sticking with a digital input, so we don’t need to worry about the noise floor of the ADC at the loudspeaker’s input.

If you have an audio signal at one of the digital inputs of the Beolab 50, and that signal is at its loudest possible level (for a sine wave, that’s 0 dB FS; or 0 dB relative to Full Scale). At Beolab 50’s maximum volume setting, this will produce a peak output level of 122 dB SPL (depending on the frequency as I mentioned above).

All digital inputs of the Beolab 50 accept at least a 24 bit word length. This means that the dynamic range of the digital input signal itself is about 6 * 24 – 3 = 141 dB. This in turn means that the hypothetical noise floor of a correctly-dithered 24-bit signal is 19 dB below the noise floor of the loudspeakers even at their maximum volume setting. (because 122 – 141 = -19)

In other words, if we assume that the streamer has a correctly-implemented gain function for its volume control, using TPDF dither implemented at the 24-bit level, then its noise floor will be 19 dB below the “natural” noise floor of the Beolab 50. Therefore, if the volume is controlled in the streamer, any artefacts will be masked by the 50s themselves.

On the other hand, the Beolab 50s volume control is done using a gain function that is performed in a 32-bit floating point calculation, which means that it has a dynamic range of 144 to 150 dB. (See this posting for an explanation and comparison of fixed point and floating point systems.) So the noise generated by the internal volume control will be somewhere between 22 and 26 dB below the “natural” noise floor of the Beolab 50.

So, (assuming my assumptions are correct) the noise floor that is produced by controlling the volume control in either the streamer or the Beolab 50s is FAR below the constant noise floor of the DAC / amplifiers.

In addition, the noise floors have roughly the same spectra (in other words, you don’t have pink noise in one case but white noise in the other; they’re all producing white noise). And since both are so far below, it really doesn’t matter. Arguing about whether the noise is 19 dB lower or 22 dB lower is a waste of good argument time, unless you paid for the four-and-a-half-hour argument instead of the five-minute one…

Important Notes

If the customer was asking about using the analogue input, then the answer MIGHT have been different.

Also, if my assumption about a 24-bit signal coming from the streamer, or that it has a correctly-implemented gain function for its volume control are incorrect, the this answer MIGHT be incorrect as well.

Excursion vs. Frequency

Last week, I was doing a lecture about the basics of audio and I happened to mention one of the rules of thumb that we use in loudspeaker development:

If you have a single loudspeaker driver and you want to keep the same Sound Pressure Level (or output level) as you change the frequency, then if you go down one octave, you need to increase the excursion of the driver 4 times.

One of the people attending the presentation asked “why?” which is a really good question, and as I was answering it, I realised that it could be that many people don’t know this.

Let’s take this step-by-step and keep things simple. We’ll assume for this posting that a loudspeaker driver is a circular piston that moves in and out of a sealed cabinet. It is perfectly flat, and we’ll pretend that it really acts like a piston (so there’s no rubber or foam surround that’s stretching back and forth to make us argue about changes in the diameter of the circle). Also, we’ll assume that the face of the loudspeaker cabinet is infinite to get rid of diffraction. Finally, we’ll say that the space in front of the driver is infinite and has no reflective surfaces in it, so the waveform just radiates from the front of the driver outwards forever. Simple!

Then, we’ll push and pull the loudspeaker driver in and out using electrical current from a power amplifier that is connected to a sine wave generator. So, the driver moves in and out of the “box” with a sinusoidal motion. This can be graphed like this:

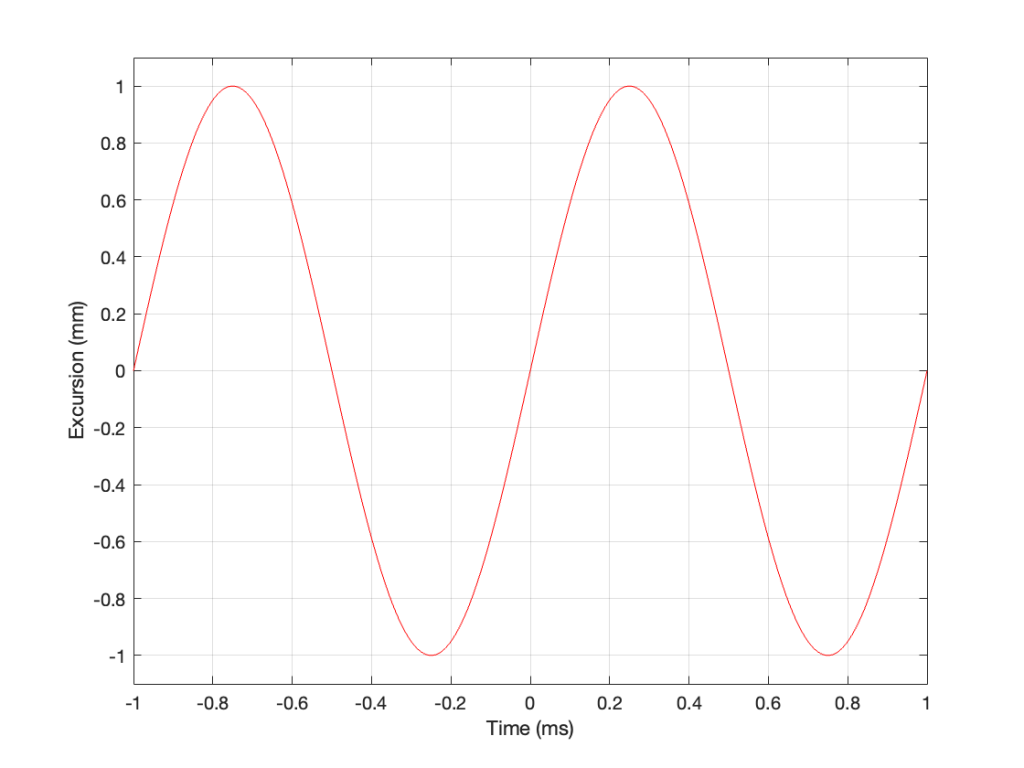
Figure 1: The excursion of a loudspeaker driver playing a 1 kHz sine wave at some output level.

As you can see there, we have one cycle per millisecond, therefore 1000 cycles per second (or 1 kHz), and the driver has a peak excursion of 1 mm. It moves to a maximum of 1 mm out of the box, and 1 mm into the box.

Consider the wave at Time = 0. The driver is passing the 0 mm line, going as fast as it can moving outwards until it gets to 1 mm (at Time = 0.25 ms) by which time it has slowed down and stopped, and then starts moving back in towards the box.

So, the velocity of the driver is the slope of the line in Figure 1, as shown in Figure 2.

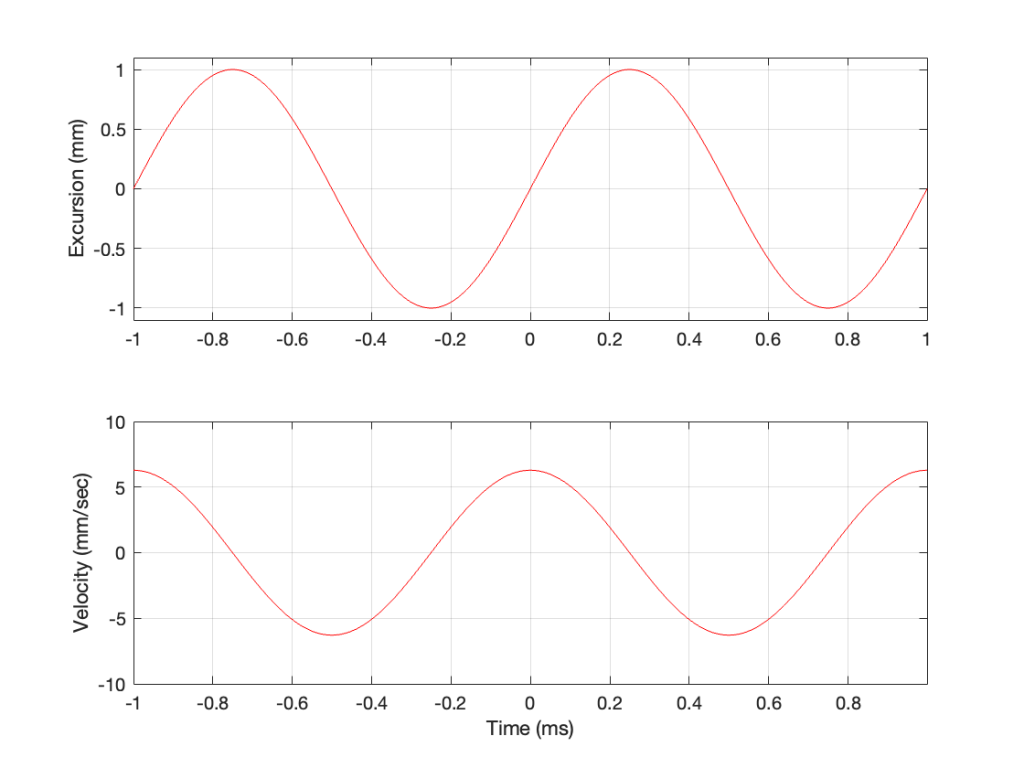
Figure 2: The excursion and velocity of the same loudspeaker driver playing the same signal.

As the loudspeaker driver moves in and out of the box, it’s pushing and pulling the air molecules in front of it. Since we’ve over-simplified our system, we can think of the air molecules that are getting pushed and pulled as the cylinder of air that is outlined by the face of the moving piston. In other words, its a “can” of air with the same diameter as the loudspeaker driver, and the same height as the peak-to-peak excursion of the driver (in this case, 2 mm, since it moves 1 mm inwards and 1 mm outwards).

However, sound pressure (which is how loud sounds are) is a measurement of how much the air molecules are compressed and decompressed by the movement of the driver. This is proportional to the acceleration of the driver (neither the velocity nor the excursion, directly…). Luckily, however, we can calculate the driver’s acceleration from the velocity curve. If you look at the bottom plot in Figure 2, you can see that, leading up to Time = 0, the velocity has increased to a maximum (so the acceleration was positive). At Time = 0, the velocity is starting to drop (because the excursion is on its was up to where it will stop at maximum excursion at time = 0.25 ms).

In other words, the acceleration is the slope of the velocity curve, the line in the bottom plot in Figure 2. If we plot this, it looks like Figure 3.

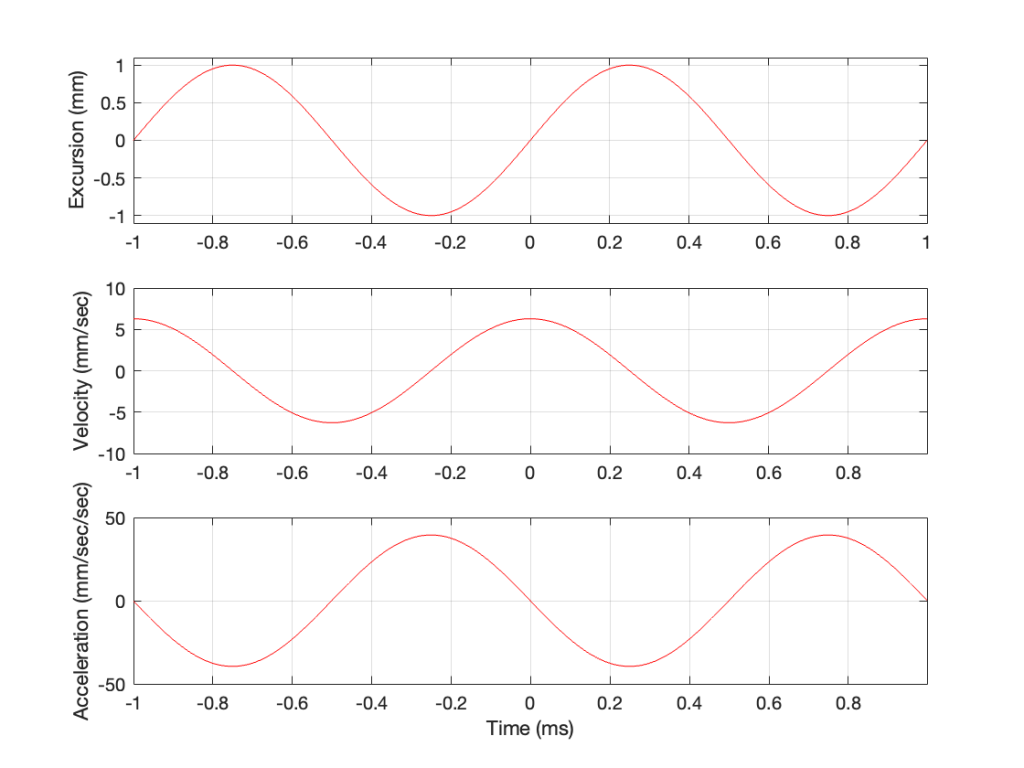
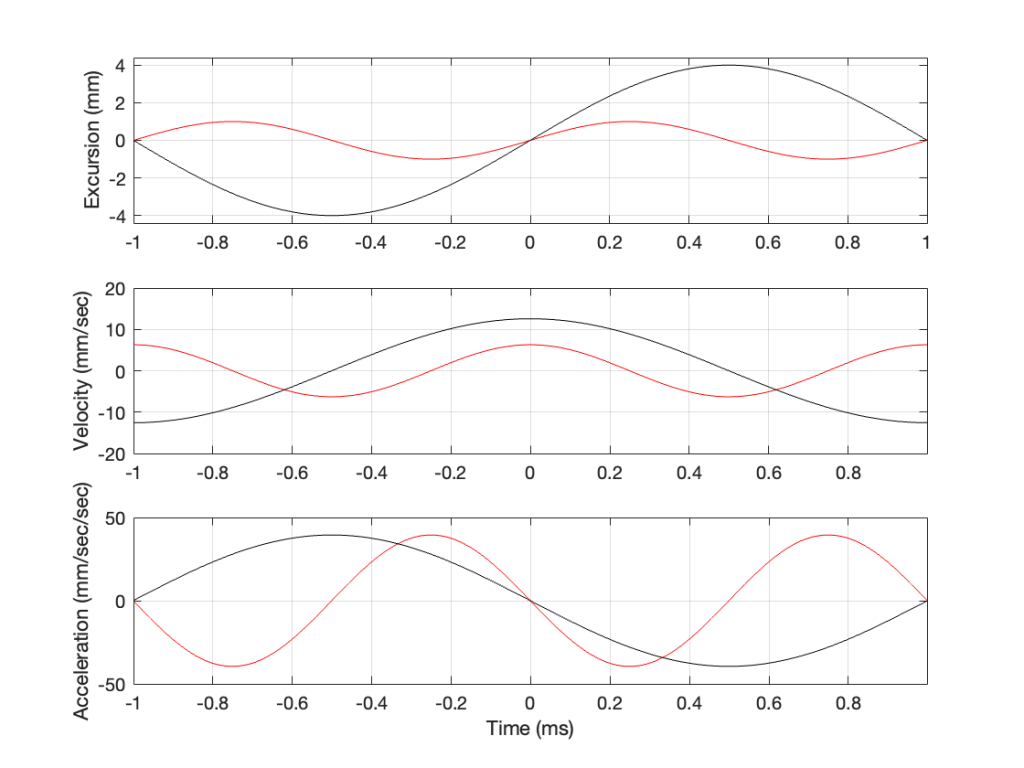
Figure 3: The excursion, velocity and acceleration of the same loudspeaker driver playing the same signal.

Now we have something useful. Since the bottom plot in Figure 3 shows us the acceleration of the driver, then it can be used to compare to a different frequency. For example, if we get the same driver to play a signal that has half of the frequency, and the same excursion, what happens?

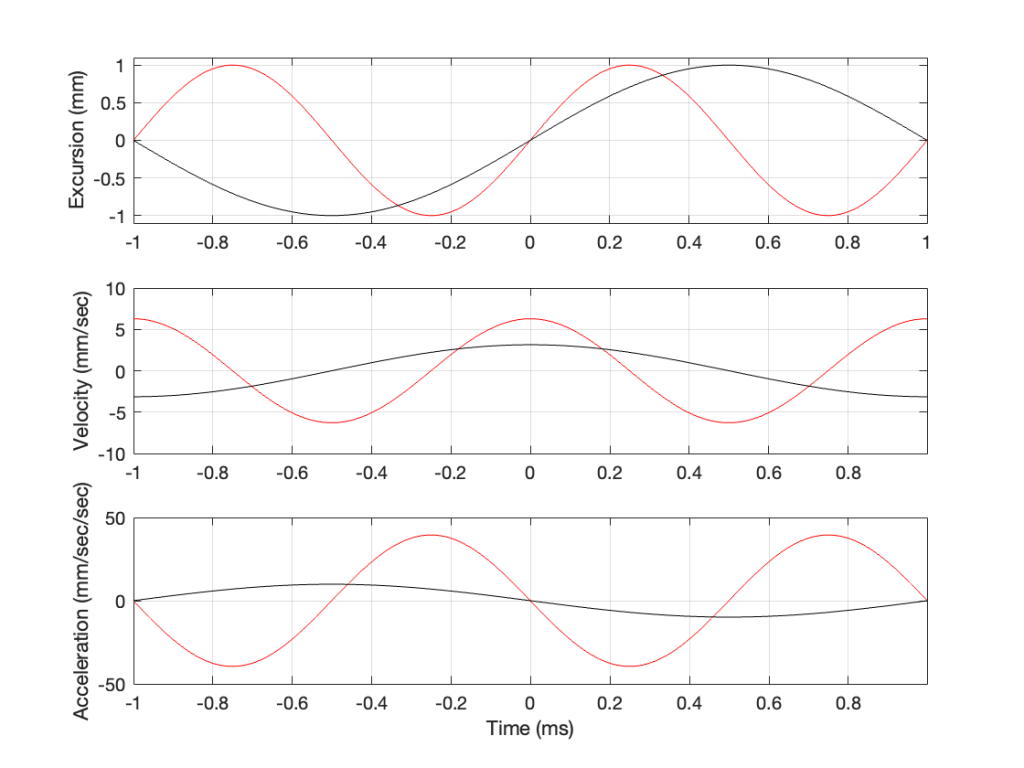
Figure 4: Comparing the excursion, velocity and acceleration of the same loudspeaker driver playing two different signals with the same excursion. (The red line is the same in Figure 4 as in Figure 3.)

In Figure 4, two sine waves are shown: the black line is 1/2 of the frequency of the red line, but they both have the same excursion. If you take a look at where both lines cross the Time = 0 point, then you can see that the slopes are different: the red line is steeper than the black. This is why the peak of the red line in the velocity curve is higher, since this is the same thing. Since the maximum slope of the red line in the middle plot is higher than the maximum slope of the black line, then its acceleration must be higher, which is what we see in the bottom plot.

Since the sound pressure level is proportional to the acceleration of the driver, then we can see in the top and bottom plots in Figure 4 that, if we halve the frequency (go down one octave) but maintain the same excursion, then the acceleration drops to 25% of the previous amount, and therefore, so does the sound pressure level (20*log10(0.25) = -12 dB, which is another way to express the drop in level…)

This raises the question: “how much do we have to increase the excursion to maintain the acceleration (and therefore the sound pressure level)?” The answer is in the “25%” in the previous paragraph. Since maintaining the same excursion and multiplying the frequency by 0.5 resulted in multiplying the acceleration by 0.25, we’ll have to increase the excursion by 4 to maintain the same acceleration.

Figure 5: Comparing the excursion, velocity and acceleration of the same loudspeaker driver playing two different signals at two different excursions. Notice that some of the vertical scales in the plots have changed. (The red line is the same in Figure 5 as in Figures 4 and 3.)

Looking at Figure 5: The black line is 1/2 the frequency of the red line. Their accelerations (the bottom plots) have the same peak values (which means that they produce the same sound pressure level). This, means that the slopes of their velocities are the same at their maxima, which, in turn, means that the peak velocity of the black line (the lower frequency) is higher. Since the peak velocity of the black line is higher (by a factor of 2) then the slope of the excursion plot is also twice as steep, which means that the peak of the excursion of the black line is 4x that of the red line. All of that is explained again in Figure 6.

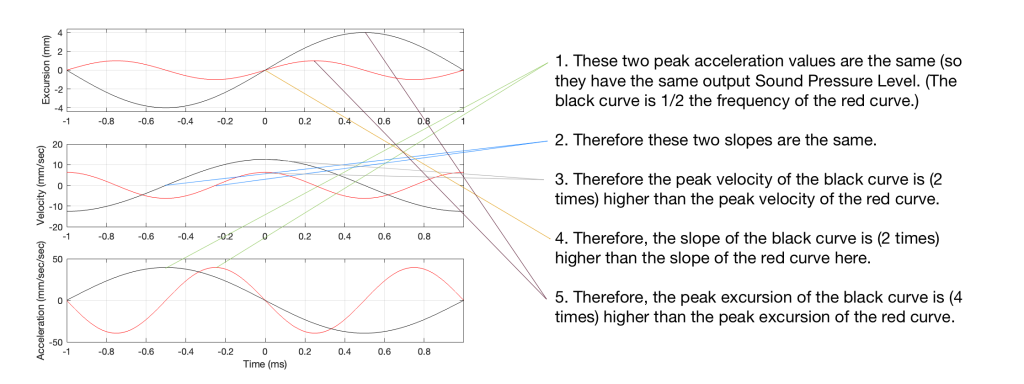
Figure 6. A repeat of Figure 5 with some explanations that (hopefully) help.

Therefore, assuming that we’re using the same loudspeaker driver, we have to increase the excursion by a factor of 4 when we drop the frequency by a factor of 2, in order to maintain a constant sound pressure level.

However, we can play a little trick… what we’re really doing here is increasing the volume of our “cylinder” of air by a factor of 4. Since we don’t change the size of the driver, we have to move it 4 times farther.

However, the volume of a cylinder is

π r2 * height

and we’re just playing with the “height” in that equation. A different way would be to use a different driver with a bigger surface area to play the lower frequency. For example, if we multiply the radius of the driver by 2, and we don’t change the excursion (the “height” of the cylinder) then the total volume increases by a factor of 4 (because the radius is squared in the equation, and 2*2 = 4).

Another way to think of this: if our loudspeaker driver was a square instead of a circle, we could either move it in and out 4 times farther OR we would make the width and the length of the square each twice as big to get the a cube with the same volume. That “r2” in the equation above is basically just the “width * length” of a circle…

This is why woofers are bigger than tweeters. In a hypothetical world, a tweeter can play the same low frequencies as a woofer – but it would have to move REALLY far in and out to do it.

Loud speaker

I live in Denmark where people speak Danish. One interesting word that I use every day is “højtaler” which is the Danish word for “loudspeaker”. I say that this word is “interesting” because, just like “loudspeaker” it is actually two words glued together. “Høj” means “high” or “loud” and “taler” means “talker” or “speaker” (as in “the person who is doing the talking”).

Sometimes, when I have a couple of minutes to spare, instead of looking at cat videos on YouTube, I sift through old audio and electronics magazines for fun. One really good source for these is the collection at worldradiohistory.com. (archive.org is also good!). Today I stumbled across the December, 1921 edition of Practical Electrics Magazine (which changed its name to The Experimenter in November of 1924 and then to Amazing Stories in April 1926*) It had a short description of a stage trick called the “Haunted Violin”, an excerpt from which is shown below.

The trick was that a violin, held by a woman walking around the aisle of the theatre would appear to play itself. In fact, as you can see above, there was an incognito violinist with a “detectophone” that was transmitting through wires connected to metal plates under the carpet in the theatre. The woman was wearing shoes with heels pointy enough to pierce the carpet and make contact with the plates. The heels were then connected with wires running through her dress to a “loud talker” hidden inside the violin.

Seems that, in 1921, it would have been easier to learn at least one word in Danish…

Side note: This is why, when I’m writing about audio systems I try as hard as possible to always use the word “loudspeaker” instead of “speaker”. To me, a “speaker” is a person giving a speech. A “loudspeaker” is a thing I complain about every day at work.

* That April 1926 edition of Amazing Stories had short stories by Jules Verne, H.G. Wells, and Edgar Allan Poe!

Post Script:
My wife reminded me that it’s the same in French: “haut-parleur”. It’s a reminder that the original loudspeakers were never intended for music, I suppose…

Volume controls vs. Output levels

#92 in a series of articles about the technology behind Bang & Olufsen

One question people often ask about B&O loudspeakers is something like ”Why doesn’t the volume control work above 50%?”.

This is usually asked by someone using a small loudspeaker listening to pop music.

There are two reasons for this, related to the facts that there is such a wide range of capabilities in different Bang & Olufsen loudspeakers AND you can use them together in a surround or multiroom system. In other words for example, a Beolab 90 is capable of playing much, much more loudly than a Beolab 12; but they still have to play together.

Let’s use the example of a Beolab 90 and a Beolab 12, both playing in a surround configuration or a multiroom setup. In both cases, if the volume control is set to a low enough level, then these two types of loudspeakers should play at the same output level. This is true for quiet recordings (shown on the left in the figure below) and louder recordings (shown on the right).

However, if you turn up the volume control, you will reach an output level that exceeds the capability of the Beolab 12 for the loud song (but not for the quiet song), shown in the figure below. At this point, for the loud song, the Beolab 12 has already begun to protect itself.

Once a B&O loudspeaker starts protecting itself, no matter how much more you turn it up, it will turn itself down by the same amount; so it won’t get louder. If it did get louder, it would either distort the sound or stop working – or distort the sound and then stop working.

If you ONLY own Beolab 12s and you ONLY listen to loud songs (e.g. pop and rock) then you might ask “why should I be able to turn up the volume higher than this?”.

The first answer is “because you might also own Beolab 90s” which can go louder, as you can see in the right hand side of the figure above.

The second answer is that you might want to listen to quieter recording (like a violin solo or a podcast). In this case, you haven’t reached the maximum output of even the Beolab 12 yet, as you can see in the left hand side of the figure above. So, you should be able to increase the volume setting to make even the quiet recording reach the limits of the less-capable loudspeaker, as shown below.

Notice, however, that at this high volume setting, both the quiet recording and the loud recording have the same output level on the Beolab 12.

So, the volume allows you to push the output higher; either because you might also own more capable loudspeakers (maybe not today – but some day) OR because you’re playing a quiet recording and you want to hear it over the sound of the exhaust fan above your stove or the noise from your shower.

It’s also good to remember that the volume control isn’t an indicator of how loud the output should be. It’s an indicator of how much quieter or louder you’re making the input signal.

The volume control is more like how far down you’re pushing the accelerator in your car – not the indication of the speedometer. If you push down the accelerator 50% of the way, your actual speed is dependent on many things like what gear you’re in, whether you’re going uphill or downhill, and whether you’re towing a heavy trailer. Similarly Metallica at volume step 70 will be much louder than a solo violin recording at the same volume step, unless you are playing it through a loudspeaker that reached its maximum possible output at volume step 50, in which case the Metallica and the violin might be the same level.

Note 1: For all of the above, I’ve said “quiet song” and “loud song” or “quiet recording” and “loud recording” – but I could just have easily as said “quiet part of the song” and “loud part of the song”. The issue is not just related to mastering levels (the overall level of the recording) but the dynamic range (the “distance” between the quietest and the loudest moment of a recording).

Note 2: I’ve written a longer, more detailed explanation of this in Posting #81: Turn it down half-way.