I made a comment on a forum this week, commenting that, if you mix loudspeakers with closed cabinets with loudspeakers with ported cabinets (or slave drivers), the end result can be a reduction in total output: less sound from more loudspeakers. Of course, the question is “why?” and the short answer is “due to the phase mismatching of the loudspeakers”.

This is the long answer.

Before we begin, we have to get an intuitive understanding of what a ported loudspeaker is. (Note that I’ll keep saying “ported loudspeaker”, but the principle also applies to loudspeakers with slave drivers, as I’ll explain later.) Before we get to a ported loudspeaker, we need to talk about Helmholtz resonators.

Take a block that’s reasonably heavy and hang it using a spring so that it looks like this:

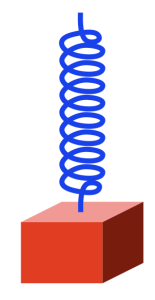
The spring is a little stretched because the weight of the block (which is the result of its mass and the Earth’s gravity) is pulling downwards. (We’ll ignore the fact that the spring is also holding up its own weight. Let’s keep this simple…) However, it doesn’t fall to the floor because the spring is pulling upwards.

Now pull downwards on the block, so it will look like the example on the right in the figure below.

The spring is stretched because we’re pulling down on the block. The spring is also pulling upwards more, since it’s pulling against the weight of the block PLUS the force that you’re adding in a downwards direction.

Now you let go of the block. What happens?

The spring is pulling “too hard” on the block, so the block starts rising back to where it started (we’ll call that the “resting position”). However, when it gets there, it has inertia (a body in motion tends to stay in motion… until it hits something big…) so it doesn’t stop. As a result, it moves upwards, higher than the resting position. This squeezes the spring until it gets to some point, at which time the block stops, and then starts going back downwards. When it returns to the resting position, it still has inertia, so it passes that point and goes too far down again. I’ve shown this as a series of positions from left to right in the figure below.

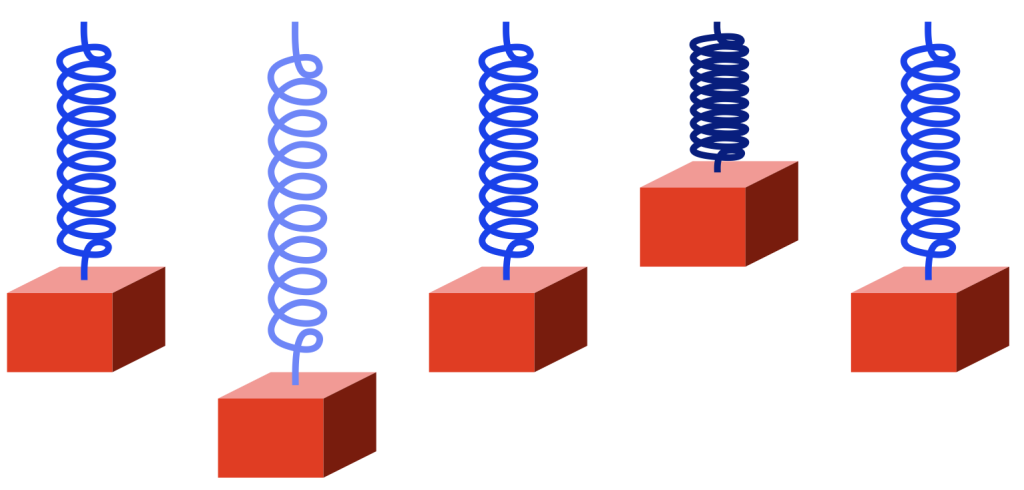
If there were no friction, no air around the block, and no friction within the metal molecules of the spring, then this would bounce up and down forever.

However, there is friction, so some of the movement (“kinetic energy”) is turned into heat and lost. So, each bounce gets smaller and smaller and the maximum velocity of the block (as it passes the resting position) gets lower and lower, until, eventually, it stops moving (at the resting position, where it started).

Notice that I changed the colour of the spring to show when it’s more stretched (lighter blue) and when it’s more compressed (darker blue).

If everything were behaving perfectly, then the RATE at which the bounce repeats wouldn’t change. Only its amplitude (or the excursion of the block, or the height of the bounce) would reduce over time. That bounce rate (let’s say 1 bounce per second, and by “bounce” I mean a full cycle of moment down, up, and back down to where it started again) is the frequency of the repetition (or oscillation).

If you make the weight lighter, then it will bounce faster (because the spring can pull the weight more “easily”). If you make the spring stiffer, then it will bounce faster (because the spring can pull the weight more “easily”). So, we can change the frequency of the oscillation by changing the weight of the block or the stiffness of the spring.

Now take a look at the same weight on a spring next to an up-side down wine bottle that (sadly) has been emptied of wine.

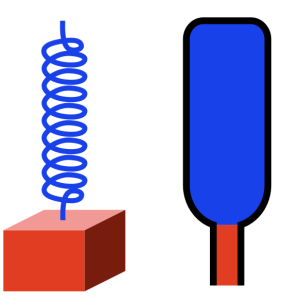
Notice that I’ve added some colours to the air inside the bottle. The air in the bottle itself is blue, just like the colour of the spring. This is because, if we pull air out of the bottle (downwards), the air inside it will pull back (upwards; just like the metal spring pulling back upwards on the block). I’ve made the small cylinder of air in the neck of the bottle red, just like the block. This is because that air has some mass, and it’s free to move upwards (into the bottle) and downwards (out of the bottle) just like the block.

If I were somehow able to pull the “plug” of air out of the neck of the bottle, the air inside would try to pull it back in. If I then “let go”, the plug would move inwards, go too far (because it also has inertia), squeezing (or compressing) the air inside the bottle, which would then push the plug back out. This is shown in the figure below.

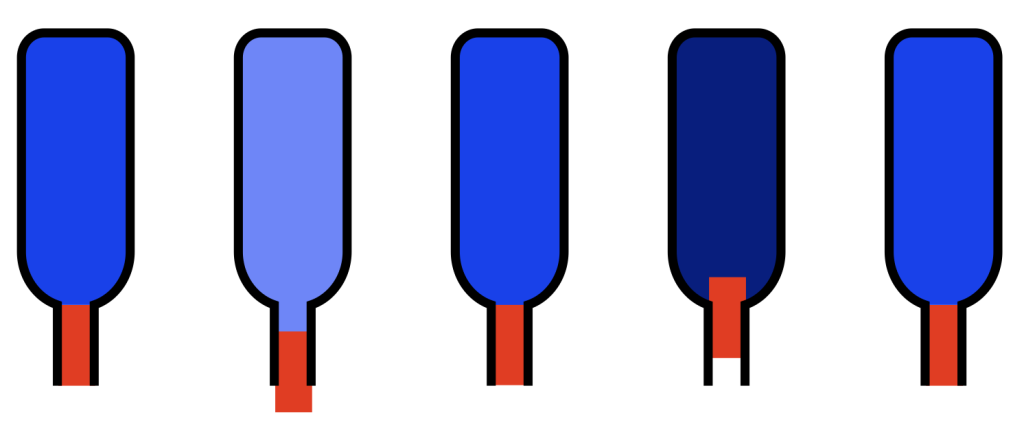
At the level we’re dealing with, this behaviour is practically identical to the behaviour of the block on the spring. In other words, although the block and the plug are made of different materials, and although the metal spring and the air inside the bottle are different materials, Figures 3 and 5 show the same behaviour of the same kind of system.

How do you pull the plug of air out of the bottle? It’s probably easier to start by pushing it inwards instead, by blowing across the top.

When you do this, a little air leaks into the opening, pushing the plug inwards. The “spring” in the bottle then pushes the plug outwards, and your cycle has started. If you wanted to do the same thing with the block, you’d lift it and let go to start the oscillation.

However, you don’t need to blow across the bottle to make it oscillate. You can just tap it with the palm of your hand, for example. Or, if you put the bottle next to your ear and listen carefully, you’ll hear a note “singing along” with the sound in the room. This is because the air in the bottle resonates; it moves back and forth very easily at the frequency that’s determined by the mass of the air in the neck and the volume of air in of the bottle (the spring).

However, remember that friction can make the oscillation decay (or die away) faster, by turning the movement into heat.

One last thing…

There’s another way to get either the block or the wine bottle oscillating:

You can move the TOP of the spring (for example, if you pull it up, then the spring will pull the block upwards, and it’ll start bouncing). Or, you could tap the bottom of the wine bottle (which is on the top in my drawings).

This method of starting the oscillation will come in handy in part 2.