In the last posting, I reviewed the math for calculating the tracking error for a radial tonearm. The question associated with this is “who cares?”
In the March, 1945 issue of Electronics Magazine, Benjamin Bauer supplied the answer. An error in the tracking angle results in a distortion of the audio signal. (This was also discussed in a 3-part article by Dr. John D. Seagrave in Audiocraft Magazine in December 1956, January 1957, and August 1957)
If the signal is a sine wave, then the distortion is almost entirely 2nd-order (meaning that you get the sine wave fundamental, plus one octave above it). If the signal is not a sine wave, then things are more complicated, so I will not discuss this.
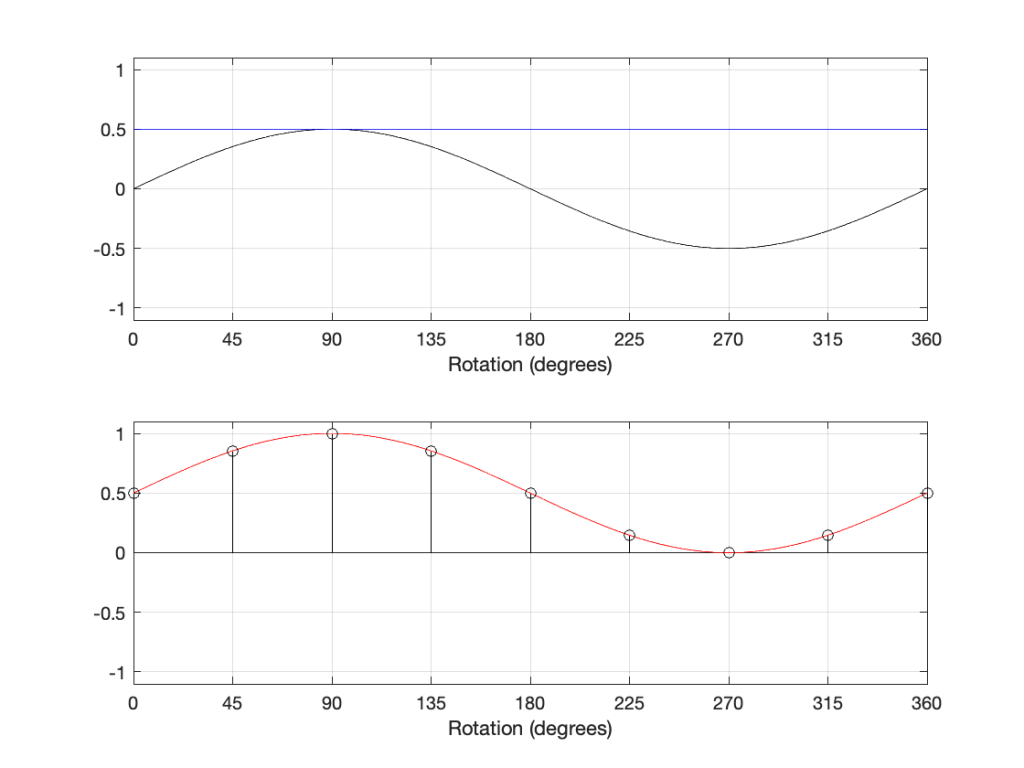
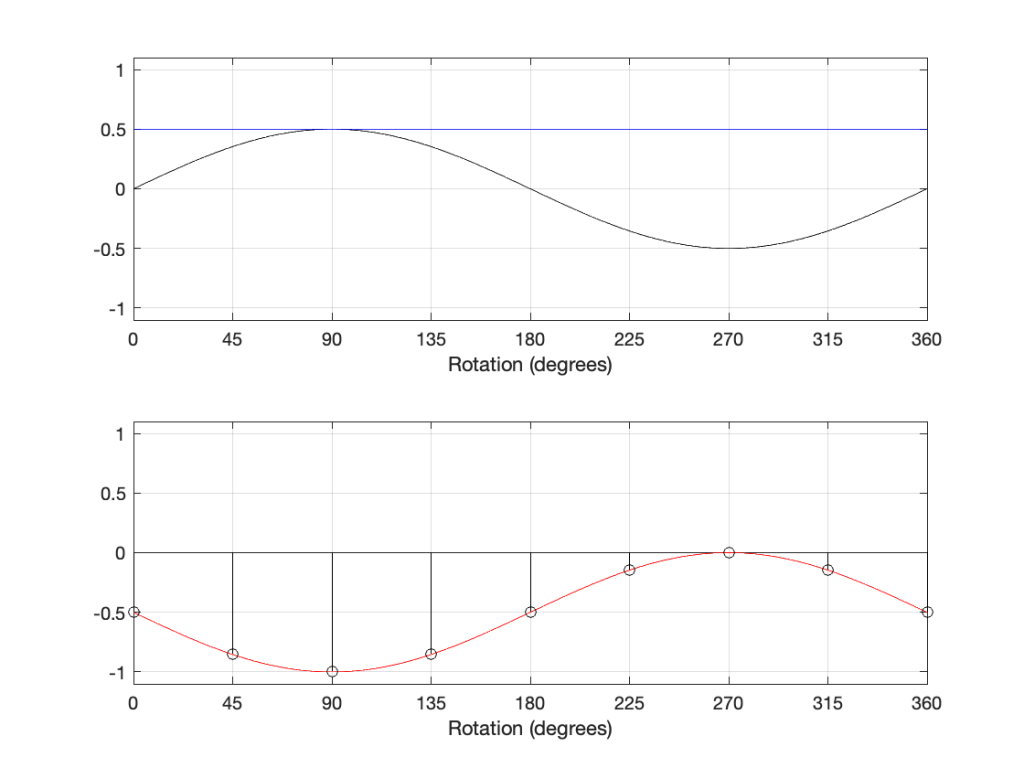
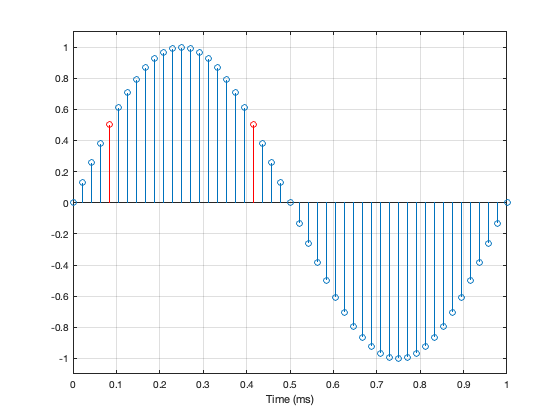
Let’s take a quick look at how the signal is distorted. An example of this is shown below.
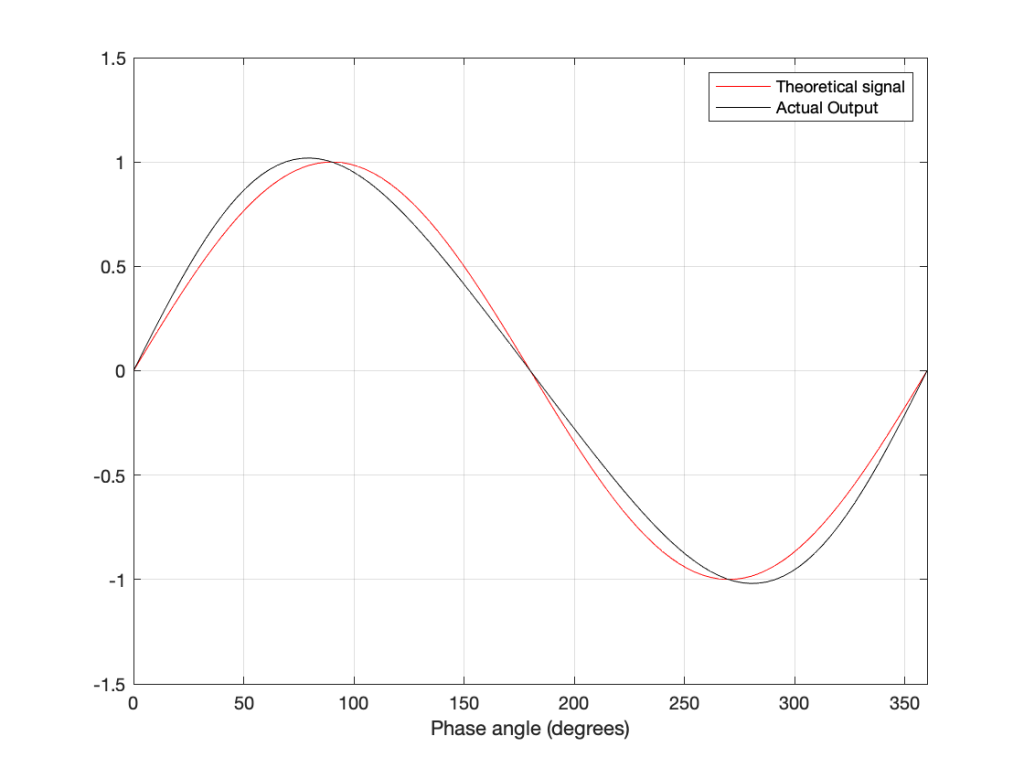
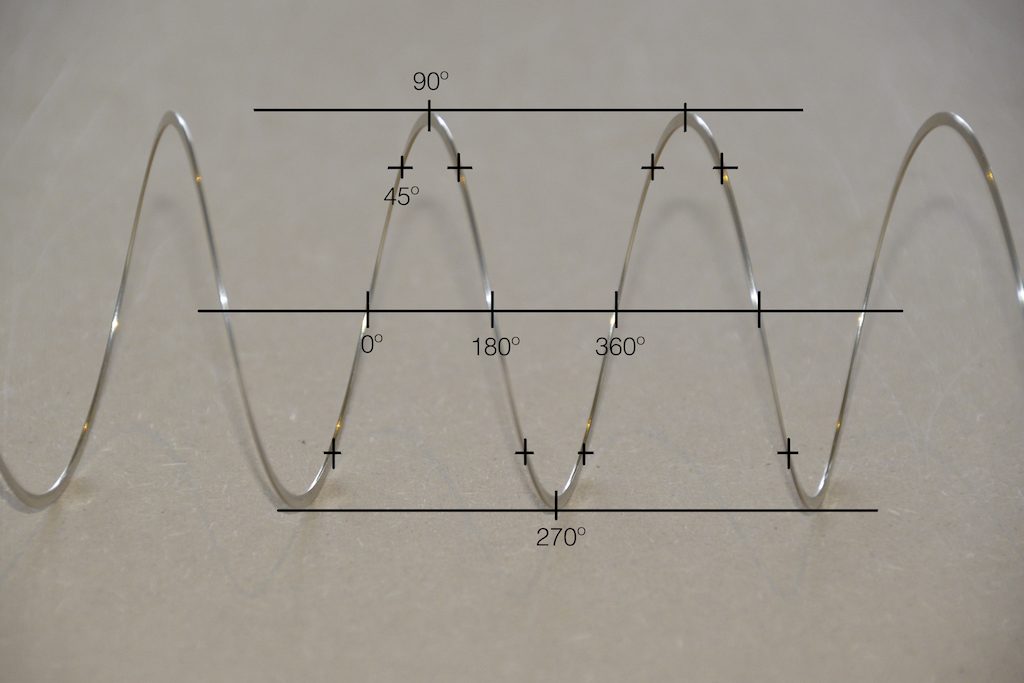
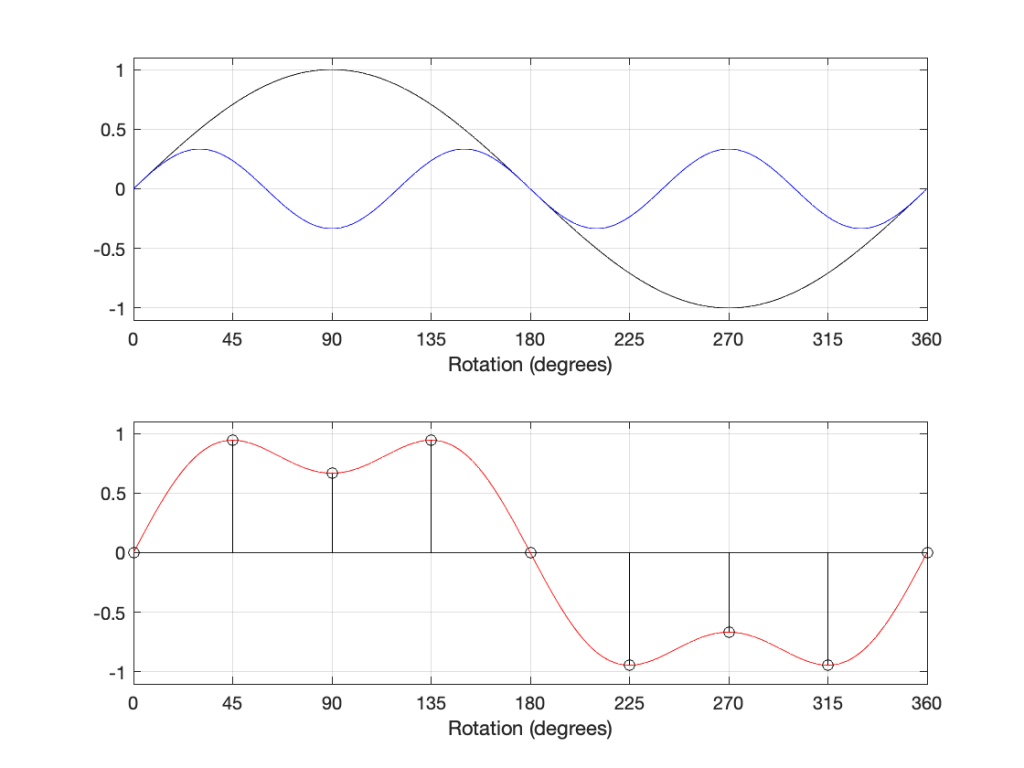
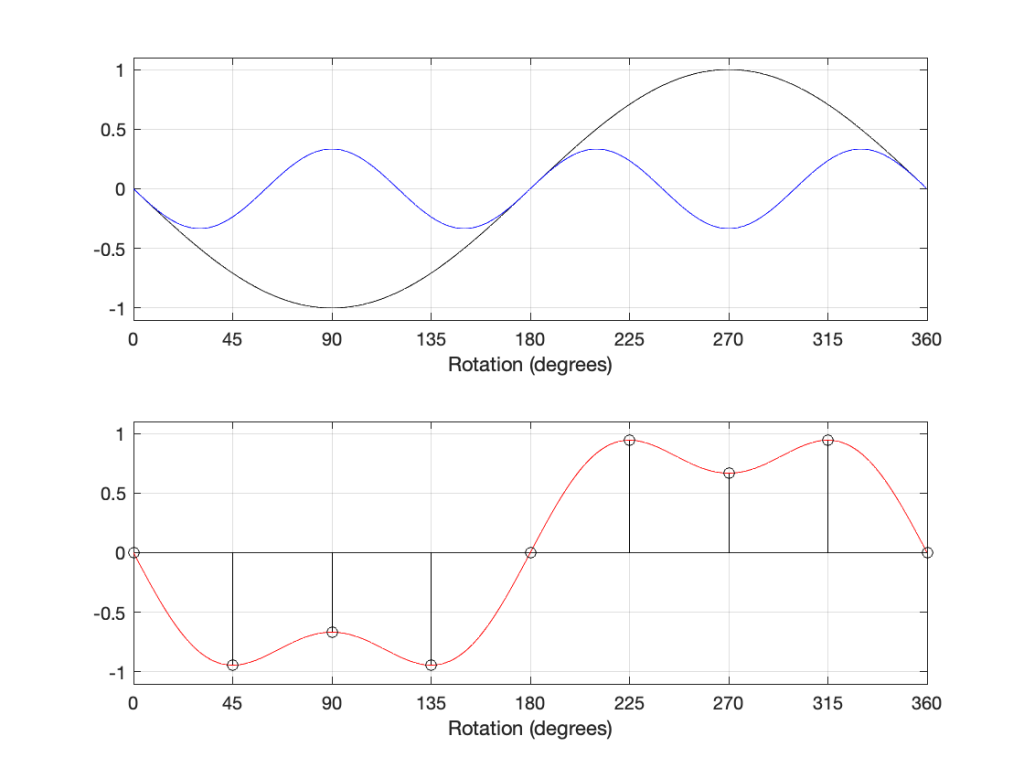
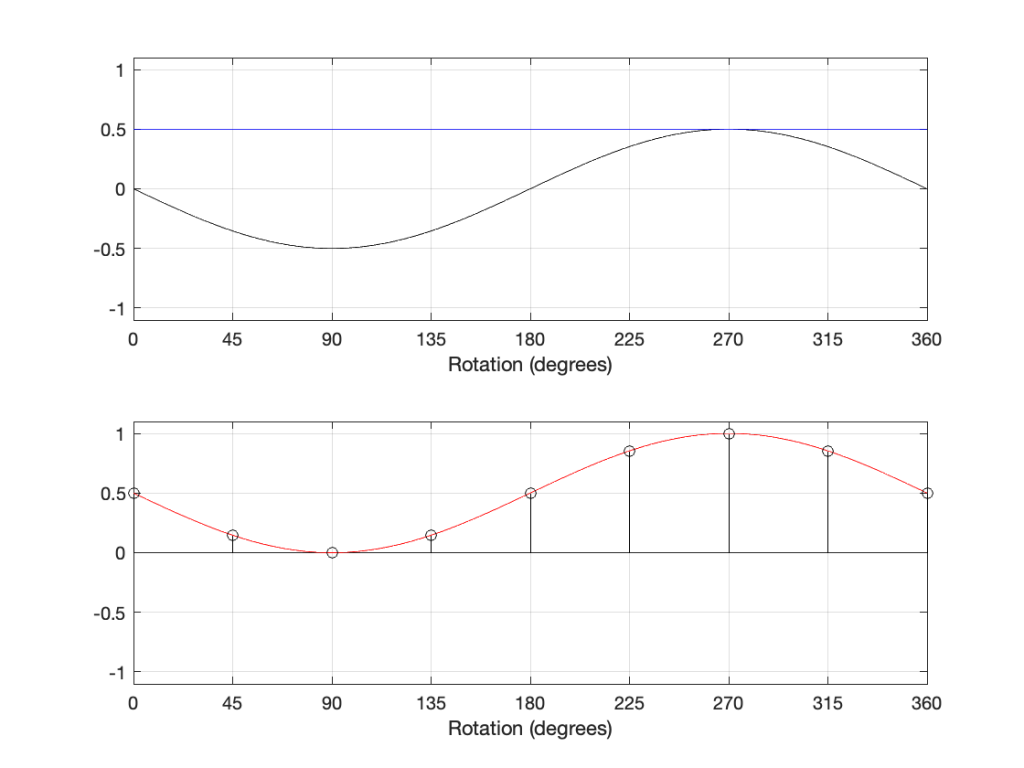
In that plot, you can see that the actual output from the stylus with a tracking error (the black curve) precedes the theoretical output that’s actually on the vinyl surface (the red curve) when the signal is positive, and lags when it’s negative. An intuitive way of thinking of this to consider the tracking error as an angular rotation, so the stylus “reads” the signal in the groove at the wrong place. This is shown below, which is merely zooming in on the figure above.
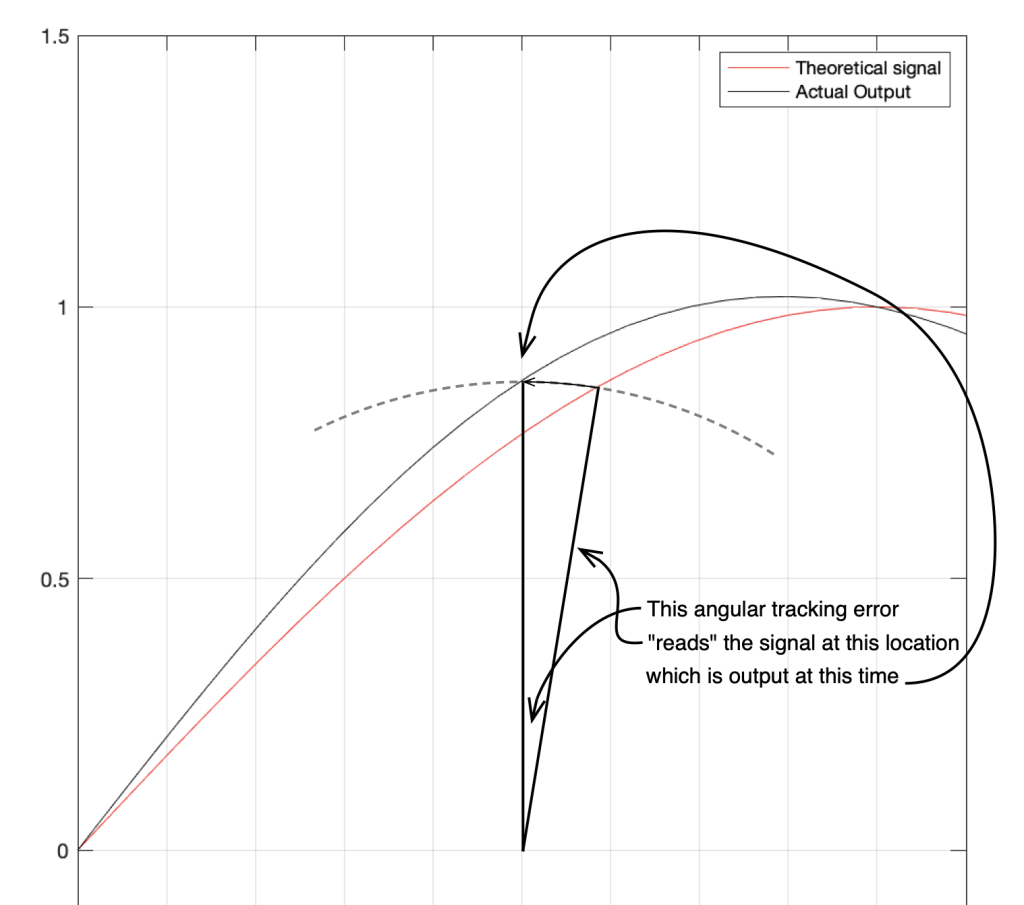
Here, you can see that the rotation (tracking error) of the stylus is getting its output from the wrong place in the groove and therefore has the wrong output at any given moment. However, the amount by which it’s wrong is dependent not only on the tracking error but the amplitude of the signal. When the signal is at 0, then the error is also 0. This is not only the reason why the distortion creates a harmonic of the sine wave, but it also explains why (as we’ll see below) the level of distortion is dependent on the level of the signal.
This intuitive explanation is helpful, but life is unfortunately, more complicated. This is because (as we saw in the previous posting), the tracking error is not constant; it changes according to where the stylus is on the surface of the vinyl.
If you dig into Bauer’s article, you’ll find a bunch of equations to help you calculate how bad things get. There are some minor hurdles to overcome, however. Since he was writing in the USA in 1945, his reference was 78 RPM records and his examples are all in inches. However, if you spend some time, you can convert this to something more useful. Or, you could just trust me and use the information below.
In the case of a sinusoidal signal the level of the 2nd harmonic distortion (in percent) can be calculated with the following equation:
PercentDistortion = 100 * (ω Αpeak α) / (ωr r)
where
- ω is 2 * pi * the audio frequency in Hz
- Apeak is the peak amplitude of the modulation (the “height” of the groove) in mm
- α is the tracking error in radians
- ωr is the rotational speed of the record in radians per second, calculated using 2 * pi * (RPM / 60)
- r is the radius of the groove; the distance from the centre spindle to the stylus in mm
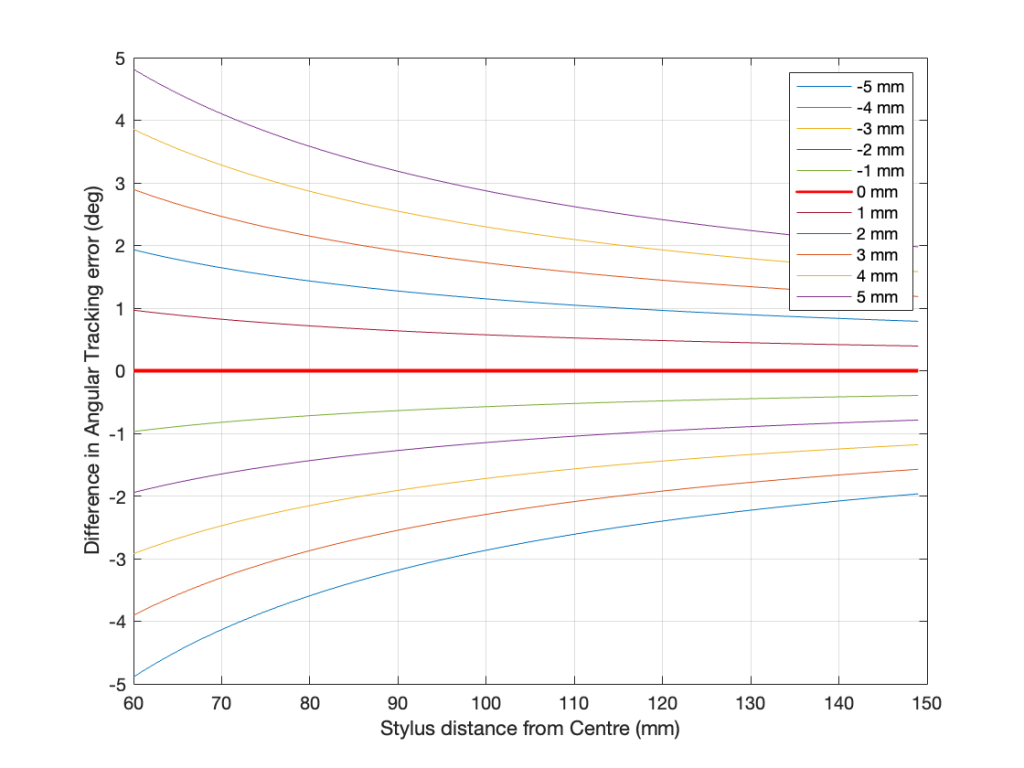
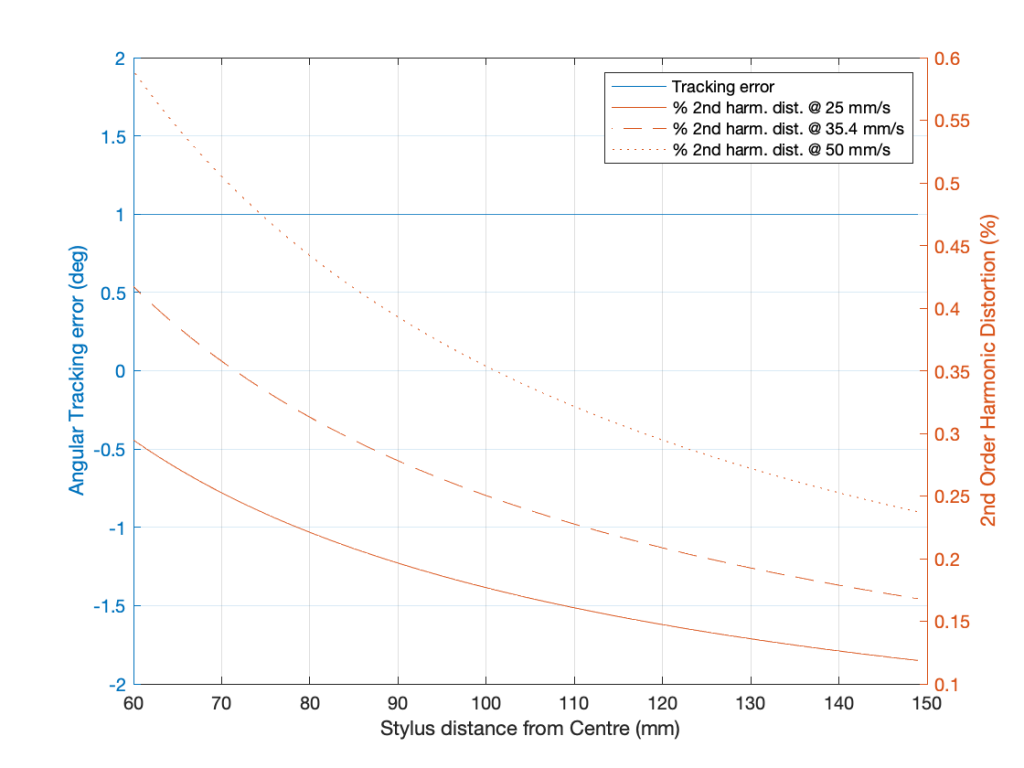
Let’s invent a case where you have a constant tracking error of 1º, with a rotational speed of 33 1/3 RPM, and a frequency of 1 kHz. Even though the tracking error remains constant, the signal’s distortion will change as the needle moves across the surface of the record because the wavelength of the signal on the vinyl surface changes (the rotational speed is the same, but the circumference is bigger at the outside edge of the record than the inside edge). The amount of error increases as the wavelength gets smaller, so the distortion is worse as you get closer to the centre of the record. This can be see in the shapes of the curves in the plot below. (Remember that, as you play the record, the needle is moving from right to left in those plots.)

You can also see in those plots that the percentage of distortion changes significantly with the amplitude of the signal. In this case, I’ve calculated using three different modulation velocities. The middle plot is 35.4 mm / sec, which is a typical accepted standard reference level, which we’ll call 0 dB. The other two plots have modulation velocities of -3 dB (25 mm / sec) and + 3 dB (50 mm / sec).
Sidebar: If you want to calculate the Amplitude of the modulation
Apeak = (ModulationVelocity * sqrt(2)) / (2 * pi * FrequencyInHz)
Note that this simplifies the equation for calculating the distortion somewhat.
Also, if you need to convert radians to degrees, then you can multiply by 180/pi. (about 57.3)
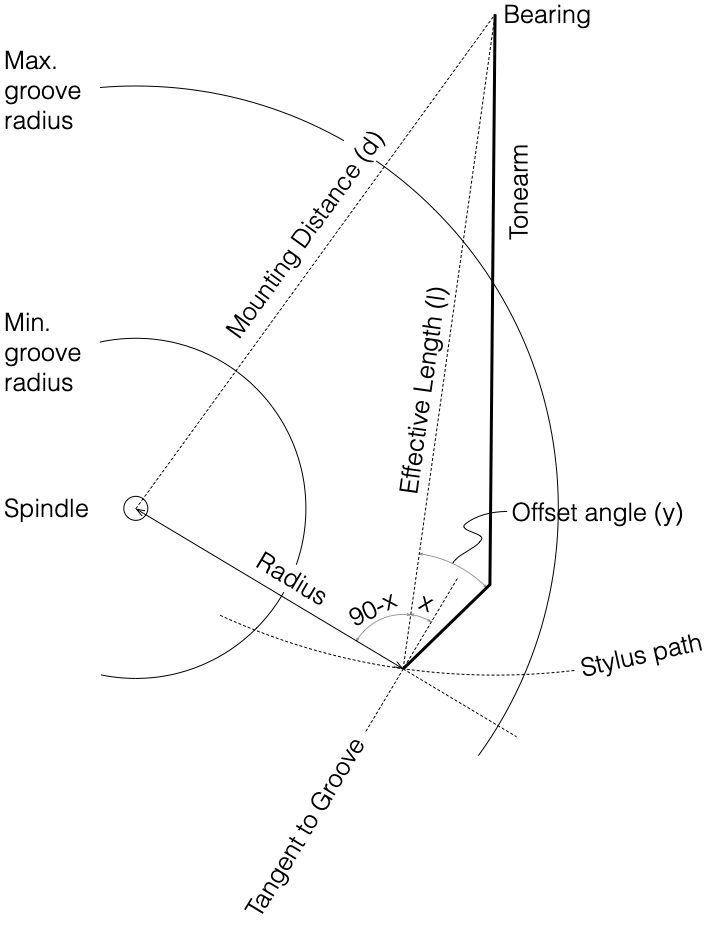
Of course, unless you have a very badly-constructed linear tracking turntable, you will never have a constant tracking error. The tracking error of a radial tonearm is a little more complicated. Using the recommended values for the “well known tonearm” that I used in the last posting:
- Effective Length (l) : 233.20 mm
- Mounting Distance (d) : 215.50 mm
- Offset angle (y) : 23.63º
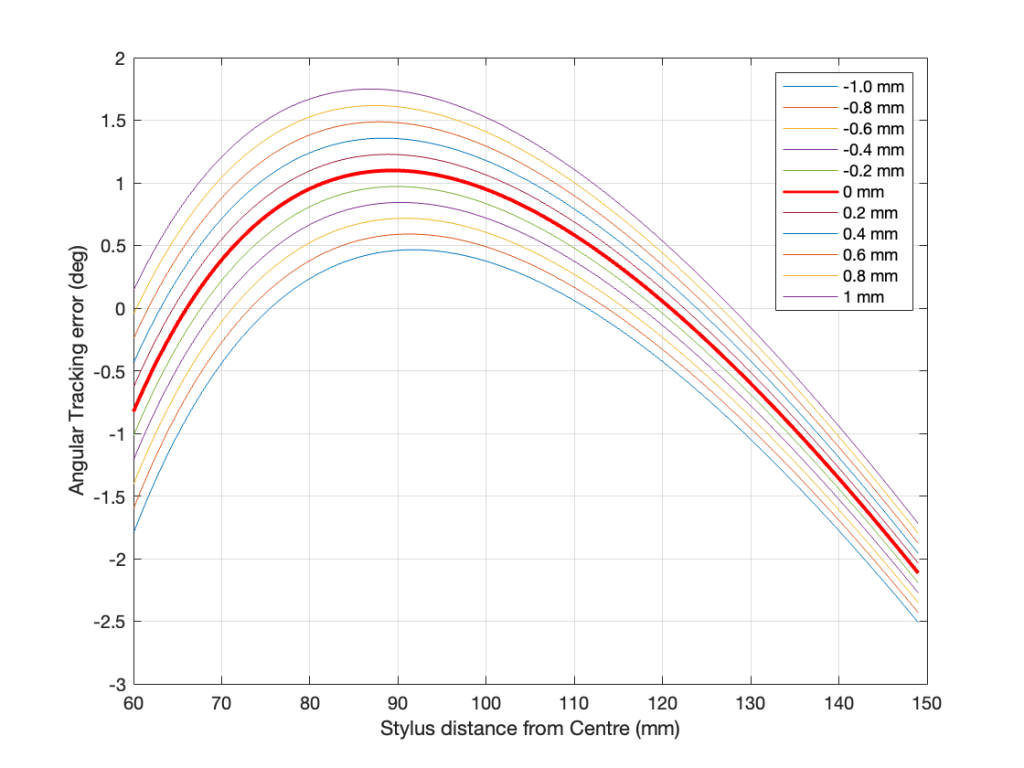
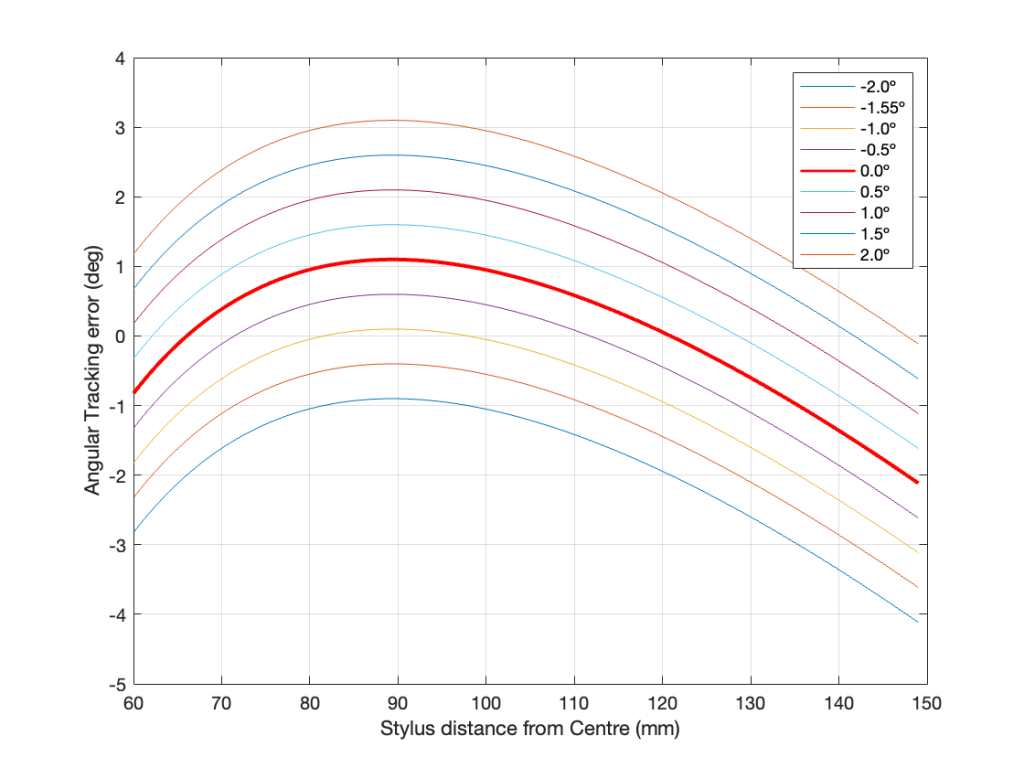
and assuming that this was done perfectly, we get the following result for a 33 1/3 RPM album.
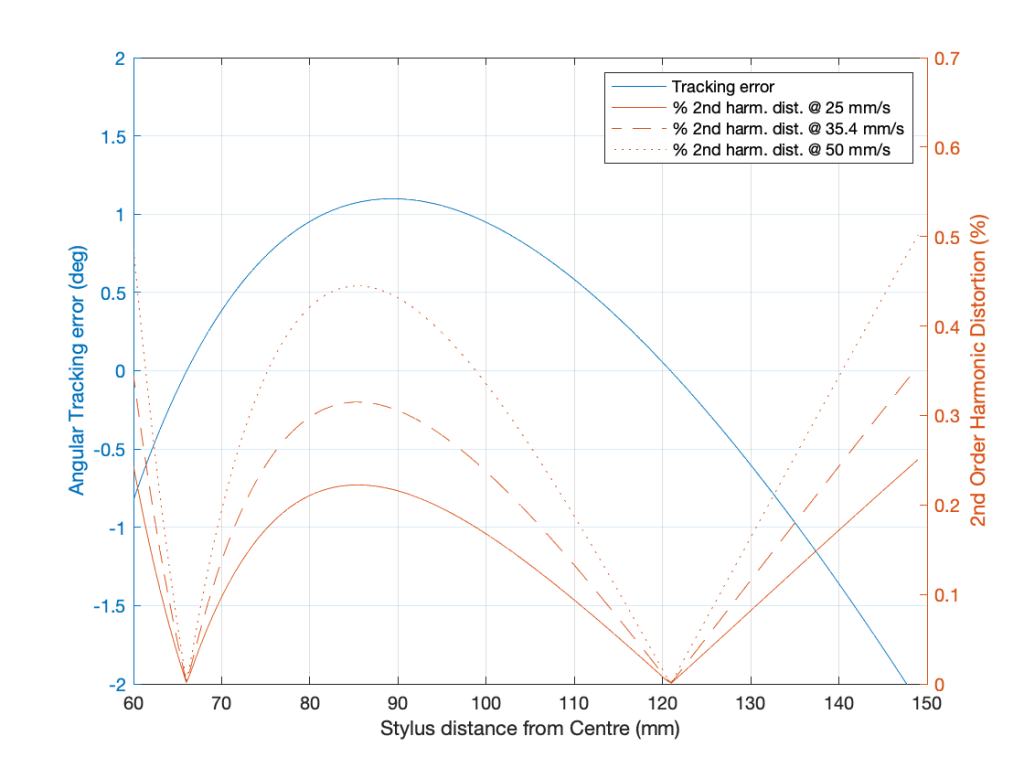
You can see here that the distortion drops to 0% when the tracking error is 0º, which (in this case) happens at two radii (distances between the centre spindle and the stylus).
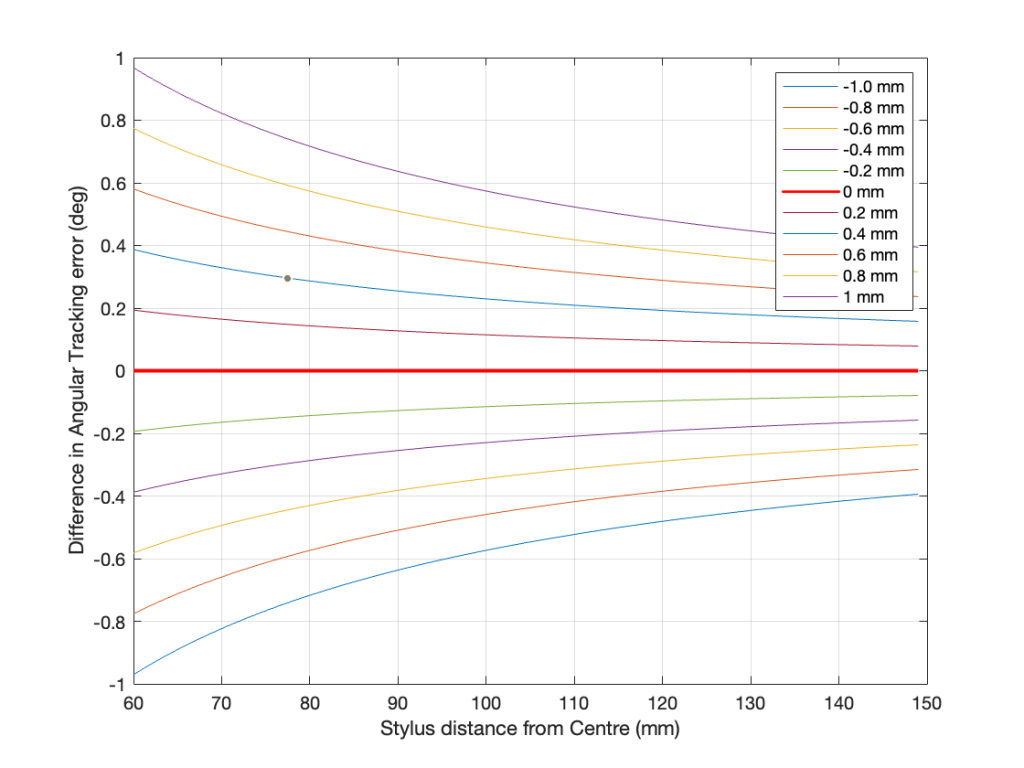
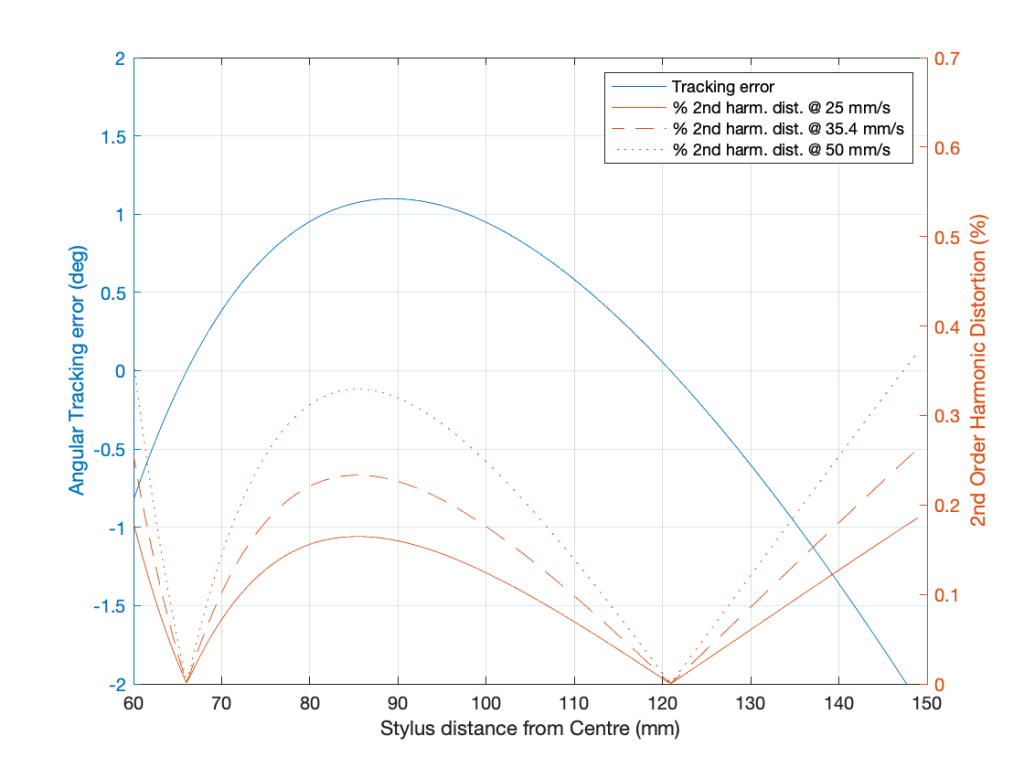
If we do exactly the same calculation at 45 RPM, you’ll see that the distortion level drops (because the value of ωr increases), as shown below. (But good luck finding a 12″ 45 RPM record… I only have two in my collection, and one of those is a test record.)
Important notes:
Everything I’ve shown above is not to be used as proof of anything. It’s merely to provide some intuitive understanding of the relationship between radial tracking tonearms, tracking error, and the resulting distortion. There is one additional important reason why all this should be taken with a grain of salt. Remember that the math that I’ve given above is for 78 RPM records in 1945. This means that they were for laterally-modulated monophonic grooves; not modern two-channel stereophonic grooves. This means that the math above isn’t accurate for a modern turntable, since the tracking error will be 45º off-axis to the axis of modulation of the groove wall. This rotation can be built into the math as a modification applied to the variable α, however, I’m not going to complicate things further today…
In addition, the RIAA equalisation curve didn’t get standardised until 1954 (although other pre-emphasis curves were being used in the 1940s). Strictly speaking, the inclusion of a pre-emphasis curve doesn’t really affect the math above, however, in real life, this equalisation makes it a little more complicated to find out what the modulation velocity (and therefore the amplitude) of the signal is, since it adds a frequency-dependent scaling factor on things. On the down-side, RIAA pre-emphasis will increase the modulation velocity of the signal on the vinyl, resulting in an increase in the distortion effects caused by tracking error. On the up-side, the RIAA de-emphasis filtering is applied not only to the fundamentals, but the distortion components as well, so the higher the order of the unwanted harmonics, the more they’ll be attenuated by the RIAA filtering. How much these two effects negate each other could be the subject of a future posting; if I can wrap my own head around the problem…
One extra comment for the truly geeky:
You may be looking at the last two plots above and being confused in the same way that I was when I made them the first time. If you look at the equation, you can see that the PercentDistortion is related to α: the tracking error. However, if you look at the plots, you’ll see that I’ve shown it as being related to | α |: the absolute value of the tracking error instead. This took me a while to deal with, since my first versions of the plots were showing a negative value for the distortion. “How can a negative tracking result in distortion being removed?” I asked myself. The answer is that it doesn’t. When the tracking error is negative, then the angle shown in the second figure above rotates counter-clockwise to the left of the vertical line. In this case, then the output of the stylus lags for positive values and precedes for negative values (opposite to the example I gave above), meaning that the 2nd-order harmonic flips in polarity. SINCE you cannot compare the phase of two sine tones that do not have the same frequency, and SINCE (for these small levels of distortion) it’ll sound the same regardless of the polarity of the 2nd-order harmonic, and SINCE (in real-life) we don’t listen to sine tones so we get higher-order THN and IMD artefacts, not just a frequency doubling, THEN I chose to simplify things and use the absolute value.
Post Script to the comment for geeks: This conclusion was confirmed by J.K. Stevenson’s article called “Pickup Arm Design” in the May, 1966 edition of Wireless World where he states “The sign of φ (positive or negative) is ignored as it has no effect on the distortion.” (He uses φ to denote the tracking error angle.)
Penultimate Post Script:
J.K. Stevenson’s article gives an alternative way of calculating the 2nd order harmonic distortion that gives the same results. However, if you are like me, then you think in modulation velocity instead of amplitude, so it’s easier to not convert on the way through. This version of the equation is
PercentDistortion = 100 * (Vpeak tan(α)) / (μ)
where
- Vpeak is the peak modulation velocity in mm/sec
- α is the tracking error in radians
- μ is the groove speed of the record in mm/sec calculated using 2*pi*(rpm/60)*r
- r is the radius of the groove; the distance from the centre spindle to the stylus in mm
Final Post-Script:
I’ve given this a lot of thought over the past couple of days and I’m pretty convinced that, since the tracking error is a rotation angle on an axis that is 45º away from the axis of modulation of the stylus (unlike the assumption that we’re dealing with a monophonic laterally-modulated groove in all of the above math), then, to find the distortion for a single channel of a stereophonic groove, you should multiply the results above by cos(45º) or 1/sqrt(2) or 0.707 – whichever you prefer. If you are convinced that this was the wrong thing to do, and you can convince me that you’re right, I’ll be happy to change it to something else.