Category: Bang & Olufsen

B&O Tech: Signal Mixing and Decomposition

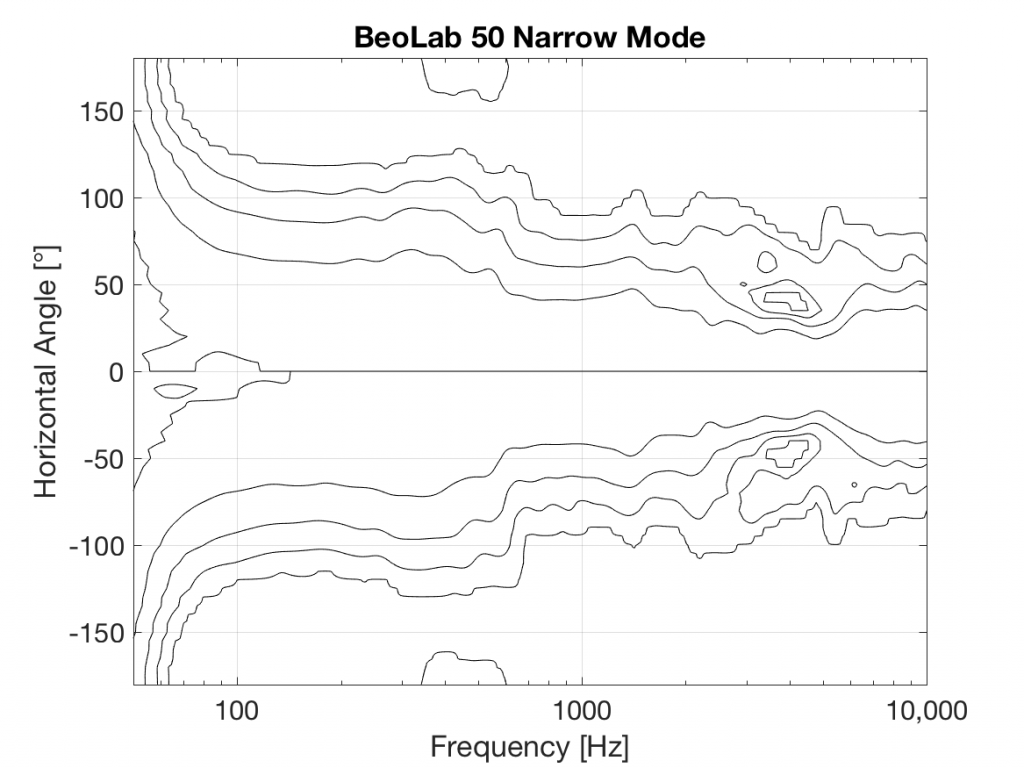
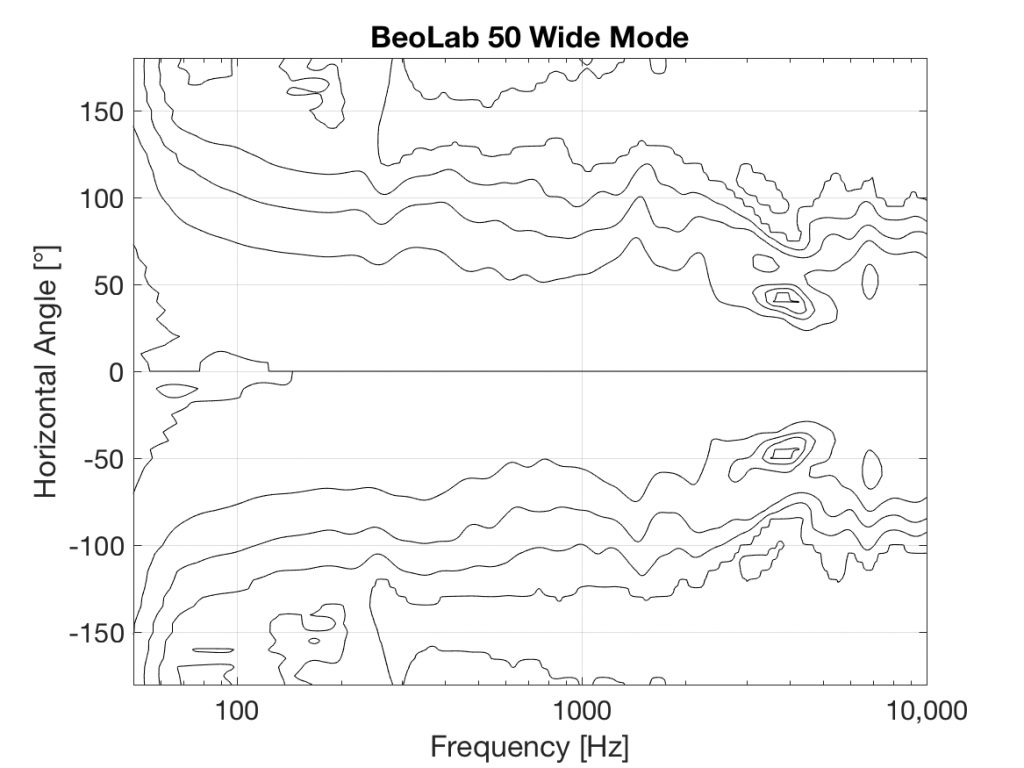
#72 in a series of articles about the technology behind Bang & Olufsen loudspeakers

After a previous posting, someone posted this as part of a comment:

“What I’ve been asking myself for a long time: how does a single driver manage to produce two or more frequencies (or a frequency range) at the exact same time? For example a singer singing while the guitar plays in the background. Could you try to explain how this works?”

So, this posting is an attempt to answer that question.

 

Adding signals together

Sound is a change of air pressure over time. That pressure is modulating on top of the day’s average barometric pressure – which is just a measurement of how closely the air particles around you are squeezed together. On a high-pressure day, the air is more densely packed – on a low pressure day, the air is less dense.

When you make a sound, you make slight variations in that pressure – so, for example, when a woofer moves out of a loudspeaker enclosure (a fancy name for “box”) then it pushes the air particles in front of it, and they’re squeezed together, resulting in a compression wave that radiates away from the loudspeaker. When the woofer pulls into the enclosure, it pulls the air particles apart, and you get a rarefaction wave instead. (You can see an animation of this at this posting.)

Let’s make a graph that shows a plot of the acoustic pressure changing over time. This is shown below in Figure 1. When this plot shows a positive number, it means that the air particles are being compressed more than normal. When it’s negative, then they’re being separated more than normal. Without getting into too many details, let’s just say that this is a low frequency. (If you want to get picky, then you’ll see that this is one cycle of a wave that takes 100 ms. Since there are 1000 ms in a second, then this must be a 10 Hertz signal, because 1000 / 100 = 10. That makes it a VERY low frequency by normal audio standards… )

Figure 1. A low frequency signal.

Let’s also look at an example of a higher frequency, shown in Figure 2, below.

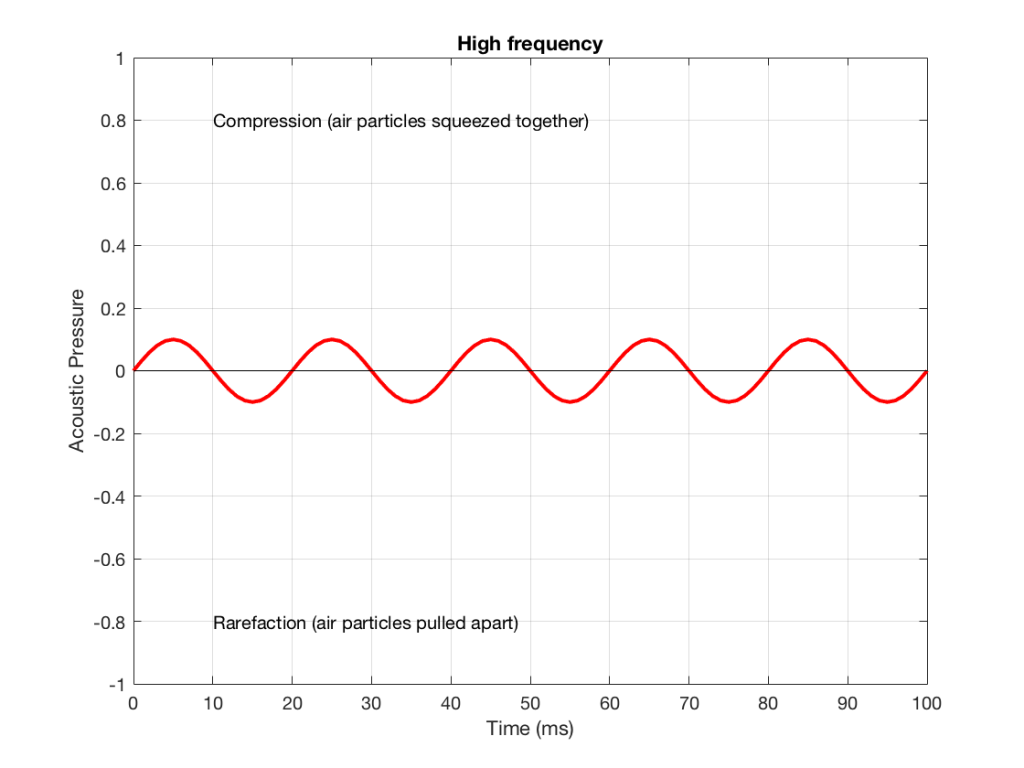
Figure 2: A signal with a higher frequency and a lower amplitude than the one shown in Figure 1.

We can see that Figure 2 has a higher frequency signal, because it moves up and down more frequently. It has 5 cycles (5 ‘ups’ and ‘downs’) in the same amount of time that it took the wave in Figure 1 to have 1 cycle – therefore it is 5 times the frequency (and therefore, if you’re being picky, 50 Hz – which, by audio standards, is also a very low frequency, but this is just an example…)

Ignoring that ACTUAL frequencies that are plotted there, let’s pretend for a moment that the low frequency (Figure 1) came from a bass guitar and the higher frequency (Figure 2) came from a singer. If we took those two signals and put them into a mixing console, what does the result look like?

Well, we take the instantaneous value of the signal at one moment in time and add it to the instantaneous value of the other signal at the same time. Let’s do that.

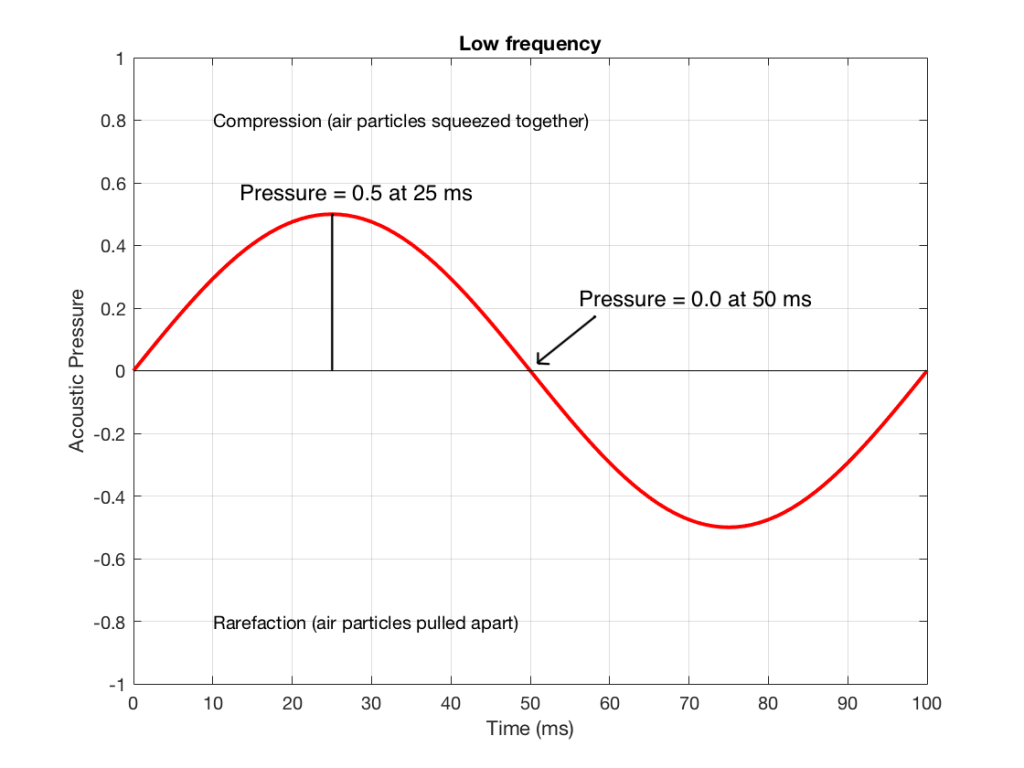
Figure 3: Some details on the signal in Figure 1.

Figure 3 shows the same signal as in Figure 1, but I’ve pointed out the values at two moments in time – at 25 ms and at 50 ms. So, for example, you can see there that, at 25 ms, the value is 0.5 – whatever that means…

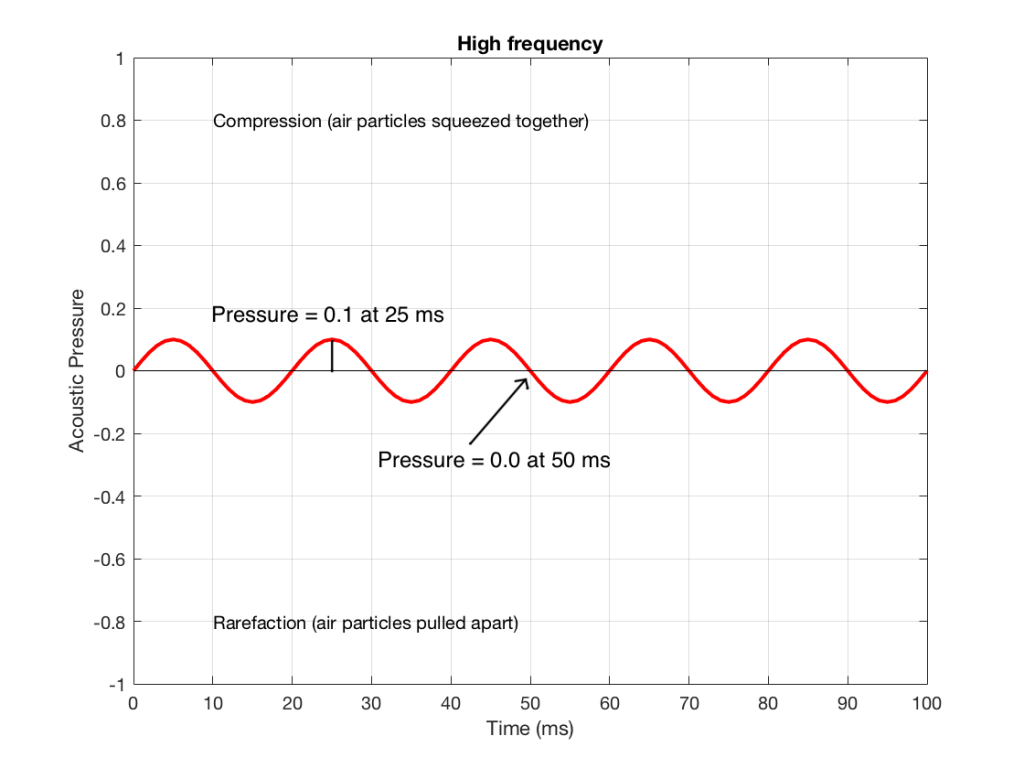
Figure 4: Some details on the signal in Figure 2.

Figure 4 shows the same signal as in Figure 2, but I’ve pointed out the values at two same moments in time – at 25 ms and at 50 ms. So, for example, you can see there that, at 25 ms, the value is 0.1 – whatever that means.

We take the value at 25 ms from each of the two signals (0.5 and 0.1) and add them together to get 0.6. This is the value of the signal at the output of the mixer at 25 ms. At 50 ms, the mixer’s output will have a value of 0 (because 0+0 = 0). This is shown graphically below for all of the values of both plots from 0 ms to 100 ms.

Figure 5: The result of adding Figures 1 and 2.

So, you can see in Figure 5 what the result will be. This signal contains both the low frequency, shown in Figure 1 and the higher frequency shown in Figure 2. If we send this combined signal to a loudspeaker, then both signals will get reproduced.

One interesting thing to note is that this mixing can also be done in the air. If a bass guitar and a singer are performing a song together, live, then the bass is pushing and pulling the molecules at the same time that the singer’s voice does. So, if at 25 ms, the bass pushes the molecules with a value of 0.5 (whatever that means) and the singer pushes the molecules with a value of 0.1, then your eardrum will be pushed in with a value of 0.6.  So, the summation of the pressure signals happens in the air, just like it does as voltages or voltage measurements in the mixing console.

 

Splitting signals apart

Typically, however, a loudspeaker is comprised of more than one driver – for example, a woofer (for the low frequencies) and a tweeter (for the high frequencies). (Of course, some loudspeakers have more than two drivers, but we’re keeping things simple today…)

So, what we do there is to put the total signal, shown in Figure 5, and send it to two circuits that change how loud things are, depending on their frequency. One circuit is called a “low pass filter” because it allows low frequencies to pass through it unchanged, but it reduces the level of higher frequencies. The other circuit is called a “high pass filter” because it allows the high frequencies to pass through it unchanged, but it reduces the level of the lower frequencies. (we won’t talk about how those circuits do that in this posting…)

We can plot the two characteristics of these two circuits – an example of which is shown in Figure 6.

Figure 6: An example of the gains applied to a signal by a low pass filter (in red) and a high pass filter (in black). Notice that, at one frequency, both filters have the same output level. That frequency is called the “crossover frequency” because it’s the frequency where the two filters’ responses cross over each other.

IF we send a signal like the one in Figure 5 to a crossover that happens to have a crossover frequency that is between the two frequencies it contains, then the signal will be split into two – one output containing mostly low-frequency components, and the other one containing mostly high-frequency components. Examples of these are shown below.

Figure 7: An example of the output of the signal from Figure 5, sent though a low-pass filter. Notice that it looks a lot like Figure 1 (the low frequency component of the combined signal) – but there’s a little bit of Figure 2 (the high frequency component) left in there…

 

Figure 8: An example of the output of the signal from Figure 5, sent though a high-pass filter. Notice that it looks a lot like Figure 2 (the high frequency component of the combined signal) – but there’s a little bit of Figure 1 (the low frequency component) left in there…

 

NB: Of course, everything I’ve shown here are just examples to make the concept intuitive. The crossover shown in Figure 6 would not work the way I’ve shown it in Figures 7 and 8 because the crossover frequency is too high compared to the 10 Hz and 50 Hz waves that I used in the example. So, please do not make comments talking about how I chose the wrong crossover frequency…

 

B&O Tech: BeoLab 50’s Beam Width Control

#65 in a series of articles about the technology behind Bang & Olufsen loudspeakers

Although active Beam Width Control is a feature that was first released with the BeoLab 90 in November of 2015, the question of loudspeaker directivity has been a primary concern in Bang & Olufsen’s acoustics research and development for decades.

As a primer, for a history of loudspeaker directivity at B&O, please read the article in the book downloadable at this site. You can read about the directivity in the BeoLab 5 here, or about the development Beam Width Control in BeoLab 90 here and here.

Bang & Olufsen has just released its second loudspeaker with Beam Width Control – the BeoLab 50. This loudspeaker borrows some techniques from the BeoLab 90, and introduces a new method of controlling horizontal directivity: a moveable Acoustic Lens.

Fig 1: BeoLab 50 PT1. The “PT” stands for ProtoType. This was the very first full-sized working model of the BeoLab 50, assembled from parts made using a 3D printer.

The three woofers and three midrange drivers of the BeoLab 50 (seen above in Figure 1) are each driven by its own amplifier, DAC and signal processing chain. This allows us to create a custom digital filter for each driver that allows us to control not only its magnitude response, but its behaviour both in time and phase (vs. frequency). This means that, just as in the BeoLab 90, the drivers can either cancel each other’s signals, or work together, in different directions radiating outwards from the loudspeaker. This means that, by manipulating the filters in the DSP (the Digital Signal Processing) chain, the loudspeaker can either produce a narrow or a wide beam of sound in the horizontal plane, according to the preferences of the listener.

Fig 2: Horizontal directivity of the BeoLab 50 in Narrow mode. Contour lines are in steps of 3 dB and are normalised to the on-axis response.

 

Fig 3: Horizontal directivity of the BeoLab 50 in Wide mode. Contour lines are in steps of 3 dB and are normalised to the on-axis response.

 

You’ll see that there is only one tweeter, and it is placed in an Acoustic Lens that is somewhat similar to the one that was first used in the BeoLab 5 in 2002. However, BeoLab 50’s Acoustic Lens is considerably different in a couple of respects.

Firstly, the geometry of the Lens has been completely re-engineered, resulting in a significant improvement in its behaviour over the frequency range of the loudspeaker driver. One of the obvious results of this change is its diameter – it’s much larger than the lens on the tweeter of the BeoLab 5. In addition, if you were to slice the BeoLab 50 Lens vertically, you will see that the shape of the curve has changed as well.

However, the Acoustic Lens was originally designed to ensure that the horizontal width of sound radiating from a tweeter was not only more like itself over a wider frequency range – but that it was also quite wide when compared to a conventional tweeter. So what’s an Acoustic Lens doing on a loudspeaker that can also be used in a Narrow mode? Well, another update to the Acoustic Lens is the movable “cheeks” on either side of the tweeter. These can be angled to a more narrow position that focuses the beam width of the tweeter to match the width of the midrange drivers.

 

Fig 4: Acoustic Lens in “narrow” mode on a later prototype of the BeoLab 50. You can see that this is a prototype, since the disc under the lens does not align very well with the top of the loudspeaker.

 

In Wide Mode, the sides of the lens open up to produce a wider radiation pattern, just as in the original Acoustic Lens.

Fig 5: Acoustic Lens in “wide” mode on a later prototype of the BeoLab 50. You can see that this is a prototype, since the disc under the lens does not align very well with the top of the loudspeaker.

 

So, the BeoLab 50 provides a selectable Beam Width, but does so not only “merely” by changing filters in the DSP, but also with moving mechanical components.

Of course, changing the geometry of the Lens not only alters the directivity, but it changes the magnitude response of the tweeter as well – even in a free field (a theoretical, infinitely large room that is free of reflections). As a result, it was necessary to have a different tuning of the signal sent to the tweeter in order to compensate for that difference and ensure that the overall “sound” of the BeoLab 50 does not change when switching between the two beam widths. This is similar to what is done in the Active Room Compensation, where a different filter is required to compensate for the room’s acoustical behaviour for each beam width. This is because, at least as far as the room is concerned, changing the beam width changes how the loudspeaker couples to the room at different frequencies.