Category: Bang & Olufsen
The Beocord 8000 Design Story
#58 in a series of articles about the technology behind Bang & Olufsen products
Cleaning up around my desk again… This time I found a booklet called the “Beocord 8000 Design Story” published by Bang & Olufsen in December of 1979. This one has some interesting information about cassette tape recorders/players – including a paper describing a cool way to measure head wear. Click here to download the file.
B&O Tech: 100 Years of Danish Loudspeakers
#56 in a series of articles about the technology behind Bang & Olufsen loudspeakers
This book was released some months ago as part of the 100 year anniversary of loudspeaker development in Denmark. There are a number of good articles in there, including a historical article on the importance of loudspeaker directivity at Bang & Olufsen.
Note that, unfortunately, the website that was associated with this book no longer exists… :-(
B&O Tech: Headphone signal flows
#54 in a series of articles about the technology behind Bang & Olufsen products
Someone recently asked a question on this posting regarding headphone loudness. Specifically, the question was:
“There is still a big volume difference between H8 on Bluetooth and cable. Why is that?”
I thought that this would make a good topic for a whole posting, rather than just a quick answer to a comment – so here goes…
Introduction – the building blocks
To begin, let’s take a quick look at all the blocks that we’re going to assemble in a chain later. It’s relatively important to understand one or two small details about each block.
Two start:
- I’ve used red lines for digital signals and blue lines for analogue signals. I’ve assumed that the digital signal contains 2 audio channels, and that the analogue connections are one channel each.
- My signal flow goes from left to right
- I use the word “telephone” not because I’m old-fashioned (although I am that…) but because if I say “phone”, I could be mistaken for someone talking about headphones. However, the source does not have to be a telephone, it could be anything that fits the descriptions below.
- The blocks in my signal flows should be taken as basic examples. I have not reverse-engineered a particular telephone or computer or pair of headphones. I’m just describing basic concepts here…
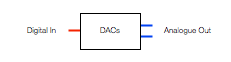
Figure 1, above, shows a 2-channel audio DAC – a Digital to Analogue Converter. This is a device (these days, it’s usually just a chip) that receives a 2-channel digital audio signal as a stream of bits at its input and outputs an analogue signal that is essentially a voltage that varies appropriately over time.
One important thing to remember here is that different DAC’s have different output levels. So, if you send a Full Scale sine wave (say, a 997 Hz, 0 dB FS) into the input of one DAC, you might get 1 V RMS out. If you sent exactly the same input into another DAC (meaning another brand or model) you might get 2 V RMS out.
You’ll find a DAC, for example, inside your telephone, since the data inside it (your MP3 and .wav files) have to be converted to an analogue signal at some point in the chain in order to move the drivers in a pair of headphones connected to the minijack output.
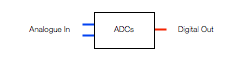
Figure 2, above, shows a 2-channel ADC – and Analogue to Digital Converter. This does the opposite of a DAC – it receives two analogue audio channels, each one a voltage that varies in time, and converts that to a 2-channel digital representation at its output.
One important thing to remember here is the sensitivity of the input of the ADC. When you make (or use) an ADC, one way to help maximise your signal-to-noise ratio (how much louder the music is than the background noise of the device itself) is to make the highest analogue signal level produce a full-scale representation at the digital output. However, different ADC’s have different sensitivities. One ADC might be designed so that 2.0 V RMS signal at its input results in a 0 dB FS (full scale) output. Another ADC might be designed so that a 0.5 V RMS signal at its input results in a 0 dB FS output. If you send 0.5 V RMS to the first ADC (expecting a max of 2 V RMS) then you’ll get an output of approximately -12 dB FS. If you send 2 V RMS to the second ADC (which expects a maximum of only 0.5 V RMS) then you’ll clip the signal.
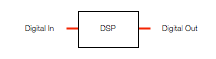
Figure 3, above, shows a Digital Signal Processor or DSP. This is just the component that does the calculations on the audio signals. The word “calculations” here can mean a lot of different things: it might be a simple volume control, it could be the filtering for a bass or treble control, or, in an extreme case, it might be doing fancy things like compression, upmixing, bass management, processing of headphone signals to make things sound like they’re outside your head, dynamic control of signals to make sure you don’t melt your woofers – anything…
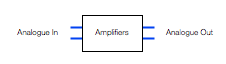
Figure 4, above, shows a two-channel analogue amplifier block. This is typically somewhere in the audio chain because the output of the DAC that is used to drive the headphones either can’t provide a high-enough voltage or current (or both) to drive the headphones. So, the amplifier is there to make the voltage higher, or to be able to provide enough current to the headphones to make them loud enough so that the kids don’t complain.
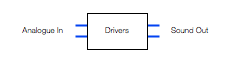
The final building block in the chain is the headphone driver itself. In most pairs of headphones, this is comprised of a circular-shaped magnet with a coil of wire inside it. The coil is glued to a diaphragm that can move like the skin of a drum. Sending electrical current back and forth through the coil causes it to move back and forth which pushes and pulls the diaphragm. That, in turn, pushes and pulls the air molecules next to it, generating high and low pressure waves that move outwards from the front of the diaphragm and towards your eardrum. If you’d like to know more about this basic concept – this posting will help.
One important thing to note about a headphone driver is its sensitivity. This is a measure of how loud the output sound is for a given input voltage. The persons who designed the headphone driver’s components determine this sensitivity by changing things like the strength of the magnet, the length of the coil of wire, the weight of the moving parts, resonant chambers around it, and other things. However, the basic point here is that different drivers will have different loudnesses at different frequencies for the same input voltage.
Now that we have all of those building blocks, let’s see how they’re put together so that you can listen to Foo Fighters on your phone.
Version 1: The good-old days
In the olden days, you had a pair of headphones with a wire hanging out of one or both sides and you plugged that wire into the headphone jack of a telephone or computer or something else. We’ll stick with the example of a telephone to keep things consistent.
Figure 6, below, shows an example of the path the audio signal takes from being a MP3 or .wav (or something else) file on your phone to the sound getting into your ears.
The file is read and then decoded into something called a “PCM” signal (Pulse Code Modulation – it doesn’t matter what this is for the purposes of this posting). So, we get to point “A” in the chain and we have audio. In some cases, the decoder doesn’t have to do anything (for example, if you use uncompressed PCM audio like a .wav file) – in other cases (like MP3) the decoder has to convert a stream of data into something that can be understood as an audio signal by the DSP. In essence, the decoder is just a kind of universal translator, because the DSP only speaks one language.
The signal then goes through the DSP, which, in a very simple case is just the volume control. For example, if you want the signal to have half the level, then the DSP just multiplies the incoming numbers (the audio signal) by 0.5 and spits them out again. (No, I’m not going to talk about dither today.) So, that gets us to point “B” in the chain. Note that, if your volume is set to maximum and you aren’t doing anything like changing the bass or treble or anything else – it could be that the DSP just spits out what it’s fed (by multiplying all incoming values by 1.0).
Now, the signal has to be converted to analogue using the DAC. Remember (from above) that the actual voltage at its output (at point “C”) is dependent on the brand and model of DAC we’re talking about. However, that will probably change anyway, since the signal is fed through the amplifiers which output to the minijack connector at point “D”.
Assuming that they’ve set the DSP so that output=input for now, then the voltage level at the output (at “D”) is determined by the telephone’s manufacturer by looking at the DAC’s output voltage and setting the gain of the amplifiers to produce a desired output.
Then, you plug a pair of headphones into the minijack. The headphone drivers have a sensitivity (a measure of the amount of sound output for a given voltage/current input) that will have an influence on the output level at your eardrum. The more sensitive the drivers to the electrical input, the louder the output. However, since, in this case, we’re talking about an electromechanical system, it will not change its behaviour (much) for different sources. So, if you plug a pair of headphones into a minijack that is supplying 2.0 V RMS, you’ll get 4 times as much sound output as when you plug them into a minijack that is supplying 0.5 V RMS.
This is important, since different devices have VERY different output levels – and therefore the headphones will behave accordingly. I regularly measure the maximum output level of phones, computers, CD players, preamps and so on – just to get an idea of what’s on the market. I’ve seen maximum output levels on a headphone jack as low as 0.28 V RMS (on an Apple iPod Nano Gen4) and as high as 8.11 V RMS (on a Behringer Powerplay Pro-8 headphone distribution amp). This is a very big difference (29 dB, which also happens to be 29 times…).
Version 2: The more-recent past
So, you’ve recently gone out and bought yourself a newfangled pair of noise-cancelling headphones, but you’re a fan of wires, so you keep them plugged into the minijack output of your telephone. Ignoring the noise-cancelling portion, the signal flow that the audio follows, going from a file in the memory to some sound in your ears is probably something like that shown in Figure 7.
As you can see by comparing Figures 7 and 6, the two systems are probably identical until you hit the input of the headphones. So, everything that I said in the previous section up to the output of the telephone’s amplifiers is the same. However, things change when we hit the input of the headphones.
The input of the headphones is an analogue to digital converter. As we saw above, the designer of the ADC (and its analogue input stages) had to make a decision about its sensitivity – the relationship between the voltage of the analogue signal at its input and the level of the digital signal at its output. In this case, the designer of the headphones had to make an assumption/decision about the maximum voltage output of the source device.
Now we’re at point “E” in the signal chain. Let’s say that there is no DSP in the headphones – no tuning, no volume – nothing. So, the signal that comes out of the ADC is sent, bit for bit, to its DAC. Just like the DAC in the source, the headphone’s DAC has some analogue output level for its digital input level. Note that there is no reason for the analogue signal level of the headphones’ input to be identical to the analogue output level of the DAC or the analogue output level of the amplifiers. The only reason a manufacturer might want to try to match the level between the analogue input and the amplifier output is if the headphones work when they’re turned off – thus connecting the source’s amplifier directly to the headphone drivers (just like in Figure 6). This was one of the goals with the BeoPlay H8 – to ensure that if your batteries die, the overall level of the headphones didn’t change considerably.
However, some headphones don’t bother with this alignment because when the batteries die, or you turn them off, they don’t work – there’s no bypass…
Version 3: Look ma! No wires!
These days, many people use Bluetooth to connect wirelessly from the source to the headphones. This means that some components in the chain are omitted (like the DAC’s in the source and the ADC in the headphones) and others are inserted (in Figures 8 and 9, the Bluetooth Transmitter and Receiver).
Note that, to keep things simple, I have not included the encoder and the decoder for the Bluetooth transmission in the chain. Depending mainly on your source’s capabilities, the audio signal will probably be encoded into one of the varieties of an SBC, an AAC, or an aptX codec before transmitting. It’s then decoded back to PCM after receiving. In theory, the output of the decoder has the same level as the input of the encoder, so I’ve left it out of this discussion. I won’t discuss either CODEC’s implications on audio quality in this posting.
Taking a look at Figure 8 or 9 and you’ll see that, in theory, the level of the digital audio signal inside the source is identical to that inside the headphones – or, at least, it can be.
This means that the potentially incorrect assumptions made by the headphone manufacturer about the analogue output levels of the source can be avoided. However, it also means that, if you have a pair of headphones like the BeoPlay H7 or H8 that can be used either via an analogue or a Bluetooth connection then there will, in many cases, be a difference in level when switching between the two signal paths.
For example…
Let’s take a simple case. We’ll build a pair of headphones that can be used in two ways. The first is using an analogue input that is processed through the headphone’s internal DSP (just as is shown in Figure 6). We’ll build the headphones so that they can be used with a 2.0 V RMS output – therefore we’ll set the input sensitivity so that a 2.0 V RMS signal will result in a 0 dB FS signal internally.
We then connect the headphones to an Apple MacBook Pro’s headphone output, we play a signal with a level of 0 dB FS, and we turn up the volume to maximum. This will result in an analogue violate level of 2.085 V RMS coming from the computer’s headphone output.
Now we’ll use the same headphones and connect them to an Apple iPhone 4s which has a maximum analogue output level of 0.92 V RMS. This is less than half the level of the MacBook Pro’s output. So, if we set the volume to maximum on the iPhone and play exactly the same file as on the MacBook Pro, the headphones will have half the output level.
A second way to connect the headphones is via Bluetooth using the signal flow shown in Figure 8. Now, if we use Bluetooth to connect the headphones to the MacBook Pro with its volume set to maximum, a 0 dB FS signal inside the computer results in a 0 dB FS signal inside the headphones.
If we connect the headphones to the iPhone 4s via Bluetooth and play the same file at maximum volume, we’ll get the same output as we did with the MacBook Pro. This is because the 0 dB FS signal inside the phone is also producing a 0 dB FS signal in the headphones.
So, if you’re on the computer, switching from a Bluetooth connection to an analogue wired connection using the same volume settings will result in the same output level from the headphones (because the headphones are designed for a max 2 V RMS analogue signal). However, if you’re using the telephone, switching from a Bluetooth connection to an analogue wired connection will results in a drop in the output level by more than 6 dB (because the telephone’s maximum output level is less than 1 V RMS).
Wrapping up
So, the answer to the initial question is that there’s a difference between the output of the H8 headphones when switching between Bluetooth and the cable because the output level of the source that you’re using is different from what was anticipated by the engineers who designed the input stage of the headphones. This is likely because the input stage of the headphones was designed to be compatible with a device with a higher maximum output level than the one you’re using.
B&O at Munich High-End
I’m on my way home from the Munich High End audio show where we were running continuous demos of the Beolab 90’s (an 8’45” mix of tracks on repeat from 10:00 a.m. to 6:00 p.m. for 4 days… It will be a while before I get the Chris Jones, Lyle Lovett and the Foo Fighters out of my head…)
We used an intentionally bare room – one Oppo Blu-ray player playing the .wav file off a USB stick, connected via S/P-DIF to the Beolab 90’s. Nothing else was in the room except three chairs, a lamp, and the people. The floor was carpeted, the ceiling was absorptive, and the walls were EXTREMELY reflective. (This helped people to hear the difference between Narrow and Wide mode – an intentional decision on my part… The room looks like a cell for someone in a straight jacket, but the listeners didn’t mind… In fact, many came back for a second listening session after hearing some of the other loudspeakers at the show…)
We spent a while the day before the show doing the Active Room Compensation measurements, and that was it – we were good to go!
The outside of the booth was simple – but the tree of Scan Speak drivers certainly attracted attention – audiophiles like drivers, apparently. :-)
Although it was nice to get out of the listening room in Struer for a while and meet some normal people – after four days on a 8’45” loop, it’s time to head home and listen to nothing for a day or two. :-)
H6 2nd Generation – Review
B&O Tech: The Beogram 4002 Design Story
#53 in a series of articles about the technology behind Bang & Olufsen products
I was cleaning up around my desk over the past week and I came across a booklet called the “Beogram 4002 Design Story” published by Bang & Olufsen in 1975. Briefly reading through it, I thought that there was a lot of general information in there that would be worth sharing for people interested in turntables. So, I got permission to post it as a PDF here. Click here to download the file.
B&O Tech: Location, Location, Location
#52 in a series of articles about the technology behind Bang & Olufsen loudspeakers
I often have to do demos of loudspeakers for people. Also, I frequently have to make recommendations on how to do (either for Bang & Olufsen dealers, or for things like press events). One of the problems that I face every time I have to do this is how to arrange the chairs so that everyone gets a reasonable impression of how a loudspeaker sounds. The problem is that this is basically impossible, due to the significant influence things like the loudspeakers’ locations, the listener location, and the room, have on the overall sound.
One aspect of how-a-loudspeaker-sounds is its magnitude response (often called a “frequency response”). A (perhaps too-simple) definition of a magnitude response is “a measure of how loud the output signal is at different frequencies if you put in a signal that is the same level at all frequencies”.
If we wanted to make a measurement of a loudspeaker’s magnitude response in a room at a particular position, we just have to put in a signal that contains all frequencies at the same magnitude (or level), capture that output with a microphone somewhere in the room, and compare how loud the signal is at different frequencies. Of course, in order to do this, we have to take care of some details. We have to make sure that the microphone (and everything else in the measurement part of the signal path) has a flat magnitude response. If it doesn’t, then at least we should know what its response is, so we can subtract it from the measurement to remove its influence on the result.
However, for the purposes of this posting, I’m not really interested in the absolute response of a loudspeaker. I’m more interested in how that response changes as you move in a room. Specifically, I want to show how much the magnitude response can change with very small changes in listening position.
Let’s start by measuring the magnitude response of a loudspeaker in a room at a location. For the purposes of this example, I’ve used a full-range, multi-way loudspeaker without a port. It’s placed roughly 1 m from the side wall and 1 m from the front wall, aimed at a listening position. The listening position is in the centre of the room’s width, and closer to the rear wall than the front wall by about a metre. The details of the location for the microphone (a 1/4″ omnidirectional measurement mic) for this measurement are shown in Figure 1, below.
I did an impulse response measurement (using an MLS signal with 4 averages (to improve SNR) and 4 sequences (to reduce the effect of distortion)) of the loudspeaker, the result of which is shown below in Figure 2. As you can see there, there are many obvious reflections after the initial impulse, and there is some kind of ringing in the room’s response.
The extremely long time before the onset of the impulse is arbitrary. The microphone was not actually 40 m away from the loudspeaker…
As I said above, I’m not interested in the resulting magnitude response of this measurement. I can tell you that it’s messy. There are bumps and dips in the low end caused (primarily) by room modes. The top end is messy due to the reflections. The overall curve is not flat due to the loudspeaker’s response, the microphone’s orientation, and various components in the signal path. However, I don’t care, since I’m not here to measure how the speaker behaves at one location in the room. I’m here to find out how its behaviour changes when you change location. So, let’s move the microphone.
As you can see in Figure 3, below, I started by moving the microphone only 100 mm, directly forwards in the room.
Again, I measured the impulse response, converted that to a magnitude response (reflections and all!), smoothed it with a running 1/3 octave smoothing and subtracted the magnitude response measured at the Reference position (also smoothed to 1/3 octave). The resulting difference is shown in Figure 4, below.
As you can see in Figure 3, moving the listening position only 100 mm results in a magnitude response deviation of about -2 to +4 dB. This is easily within the threshold of audibility for most people…
Now, let’s move the microphone sideways instead, as shown in Figure 5.
Again, a roughly 100 mm movement results in a large change in the magnitude response – although now the most significant changes have happened in the low end, as can be seen in Figure 6.
If we have more than one listener attending the demo, then I prefer to seat them “bus” style – one directly in front of the other – to ensure that everyone is getting a reasonably good phantom centre image. Sitting off-centre results in the time of arrival of signals from the two loudspeakers being mis-matched which will result in phantom images pulling towards the closer (and therefore earlier) loudspeaker.
Let’s say the we have a person roughly a half-metre behind the “good” chair, as shown in Figure 7. How different is the sound in that location?
Now we can see in Figure 8 that, by moving backwards in the room, we get more than ± 10 dB of variation in the magnitude response, with significant deviations happening as high as 1 kHz (depending on how you define “significant”).
Similarly, moving forwards by a half metre from the Reference position (shown in Figure 9) results in a similar amount of change in the magnitude response, shown in Figure 10.
Just for comparison, I’ve re-plotted the 4 magnitude response differences shown above in one plot. This is to show that the changes are not necessarily easily predicable with a simple knowledge of room layout. In other words, it would be almost impossible, without some serious simulation software, to predict these changes just by looking at a floorplan of the room and the chairs.
What’s the moral of the story here? There are many – but I’ll just mention three.
The first is the message that, even a very small change in location (like leaning to one side in your chair – or leaning forwards to rest your elbows on your knees and your chin on your hands) can dramatically change the simple magnitude response of a loudspeaker (we won’t get into the effects on the spatial behaviour of the system).
The second is that, when you’re sitting with a friend, auditioning a pair of loudspeakers, switch chairs now and again. It is extremely unlikely that you’re both hearing the same thing at the same time.
Thirdly, the fact that there are significant differences between magnitude responses at different listening positions (even within a half-metre radius) means that, if you’re doing measurements for a room compensation system using a microphone around the listening position, it’s always smarter to make more than one measurement. In fact, there are some people who argue that, in this case, having only one measurement is worse than having no measurements, since you can easily get distracted by something in the magnitude or the time response that is a problem at only that location and nowhere else.
Finally, it’s worth considering that first point a different way. Let’s say you’re the type of person who likes to tweak a stereo system by upgrading components like wires. And, let’s say that you have incredible powers of “sonic memory” – in other words, you can listen to a system, take a break, listen to it again, and you are able to detect extremely small changes in system performance (like the magnitude response). So, you listen to your system – then you get out of your chair, change the component, sit down again, and start listening to the same tune at the same level. Remember that, unless you are in exactly the same location that you were before (not just “in the same chair”…), it could be that there is a larger difference in the magnitude response of the loudspeaker due your change in position than there is due to the component you just changed… So if you are a tweaker – get someone else to do the dirty work for you so you can sit there, in your chair, with your head in a clamp, waiting to evaluate the “upgrade”…
B&O Club
This is a short Danish documentary about the B&O Club of retired B&O employees that meets weekly to restore older products for the Struer Museum.
B&O Tech: The Cube
#51 in a series of articles about the technology behind Bang & Olufsen loudspeakers
Sometimes, we have journalists visiting Bang & Olufsen in Struer to see our facilities. Of course, any visit to Struer means a visit to The Cube – our room where we do almost all of the measurements of the acoustical behaviour of our loudspeaker prototypes. Different people ask different questions about that room – but there are two that come up again and again:
- Why is the room so big?
- Why isn’t it an anechoic chamber?
Of course, the level of detail of the answer is different for different groups of people (technical journalists from audio magazines get a different level of answer than lifestyle journalists from interior design magazines). In this article, I’ll give an even more thorough answer than the one the geeks get. :-)
Introduction #1 – What do we want?
Our goal, when we measure a loudspeaker, is to find out something about its behaviour in the absence of a room. If we measured the loudspeaker in a “real” room, the measurement would be “infected” by the characteristics of the room itself. Since everyone’s room is different, we need to remove that part of the equation and try to measure how the loudspeaker would behave without any walls, ceiling or floor to disturb it.
So, this means (conceptually, at least) that we want to measure the loudspeaker when it’s floating in space.
Introduction #2 – What kind of measurements do we do?
Basically, the measurements that we perform on a loudspeaker can be boiled down into four types:
- on-axis frequency response
- off-axis frequency responses
- directivity
- power response
Luckily, if you’re just a wee bit clever (and we think that we are…), all four of these measurements can be done using the same basic underlying technique.
The very basic idea of doing any audio measurement is that you have some thing whose characteristics you’re trying to measure – the problem is that this thing is usually a link in a chain of things – but you’re only really interested in that one link. In our case, the things in the audio chain are electrical (like the DAC, microphone preamplifier, and ADC) and acoustical (like the measurement microphone and the room itself).
The computer sends a special signal (we’ll come back to that…) out of its “sound card” to the input of the loudspeaker. The sound comes out of the loudspeaker and comes into the microphone (however, so do all the reflections from the walls, ceiling and floor of the Cube). The output of the microphone gets amplified by a preamplifier and sent back into the computer. The computer then “looks at” the difference between the signal that it sent out and the signal that came back in. Since we already know the characteristics of the sound card, the microphone and the mic preamp, then the only thing remaining that caused the output and input signals to be different is the loudspeaker.
Introduction #3 – The signal
There are lots of different ways to measure an audio device. One particularly useful way is to analyse how it behaves when you send it a signal called an “impulse” – a click. The nice thing about a theoretically perfect click is that it contains all frequencies at the same amplitude and with a known phase relationship. If you send the impulse through a device that has an “imperfect” frequency response, then the click changes its shape. By doing some analysis using some 200-year old mathematical tricks (called “Fourier analysis“), we can convert the shape of the impulse into a plot of the magnitude and phase responses of the device.
So, we measure the way the device (in our case, a loudspeaker) responds to an impulse – in other words, its “impulse response”.
There are three things to initially notice in this figure.
- The first is the time before the first impulse comes in. This is the time it takes the sound to travel from the loudspeaker to the microphone. Since we normally make measurements at a distance of 3 m, this is about 8.7 ms.
- The second is the fact that the impulse doesn’t look perfect. That’s because it isn’t – the loudspeaker has made it different.
- The third is the presence of the wall reflection. (In real life, we see 6 of these – 4 walls, a ceiling and the floor – but this example is a simulation that I created, just to show the concept.)
In order to get a measurement of the loudspeaker in the absence of a room, we have to get rid of those reflections… In this case, all we have to do is to tell the computer to “stop listening” before that reflection arrives. The result is the impulse response of the loudspeaker in the absence of any reflections – which is exactly what we want.
- We make this measurement “on-axis” (usually directly in front of the loudspeaker, at some specific height which may or may not be the same height as the tweeter) to get a basic idea to begin with.
- We can then rotate the crane (the device hanging from the ceiling that the loudspeaker is resting on) with a precision of 1º. This allows us to make an off-axis measurement at any horizontal angle.
- In order to find the loudspeaker’s directivity (like Figure 5, 6, and 7 in this posting), we start by making a series of measurements (typically, every 5º for all 360º around the loudspeaker). We then tell the computer to compare the difference between each off-axis measurement and the on-axis measurement (because we’re only interested in how the sound changes with rotation – not its actual response at a given off-axis angle – we already got that in the previous measurement.
- Finally, we have to get the power response. This one is a little more tricky. The power response is the behaviour of the loudspeaker when measured in all directions simultaneously. Think of this as putting the loudspeaker in the centre of a sphere with a diameter of 3 m made of microphones. We send a signal out of the loudspeaker and measure the response at all points on the sphere, add them all together and see what the total is. This is an expensive way to do this measurement, since microphones cost a lot… An easier way is to use one microphone and rotate the loudspeaker (both horizontally and vertically) and do a LOT of off-axis measurements – not just rotating around the loudspeaker, but also going above and below it. We do each of these measurements individually, and then add the results to get a 3D sum of all responses in all directions. That total is the power response of the loudspeaker – a measurement of the total energy the loudspeaker radiates into the room.
The original questions…
Great. That’s a list of the basic measurements that come out of The Cube. However, I still have’t directly answered the original questions…
Let’s take the second question first: “Why isn’t The Cube an anechoic chamber?”
This raises the question: “What’s an anechoic chamber?” An anechoic chamber is a room whose walls are designed to be absorptive (typically to sound waves, although there are some chambers that are designed to absorb radio waves – these are for testing antennae instead of loudspeakers). If the walls are perfectly absorptive, then there are no reflections, and the loudspeaker behaves as if there are no walls.
So, this question has already been answered – albeit indirectly. We do an impulse response measurement of the loudspeaker, which is converted to magnitude and phase response measurements. As we saw in Figure 5, the reflections off the walls are easily visible in the impulse response. Since, after the impulse response measurement is done, we can “delete” the reflection (using a process called “windowing”) we end up with an impulse response that has no reflections. This is why we typically say that The Cube is “pseudo-anechoic” – the room is not anechoic, but we can modify the measurements after they’re done to be the same as if it were.
Now to the harder question to answer: “Why is the room so big?”
Let’s say that you have a device (for example, a loudspeaker), and it’s your job to measure its magnitude response. One typical way to do this is to measure its impulse response and to do a DFT (or FFT) on that to arrive at a magnitude response.
Let’s also say that you didn’t do your impulse response measurement in a REAL free field (a space where there are no reflections – the wave is free to keep going forever without hitting anything) – but, instead, that you did your measurement in a real space where there are some reflections. “No problem,” you say “I’ll just window out the reflections” (translation: “I’ll just cut the length of the impulse response so that I slice off the end before the first reflection shows up.”)
This is a common method of making a “pseudo-anechoic” measurement of a loudspeaker. You do the measurement in a space, and then slice off the end of the impulse response before you do an FFT to get a magnitude response.
Generally speaking, this procedure works fairly well… One thing that you have to worry about is a well-known relationship between the length of the impulse response (after you’ve sliced it) and the reliability of your measurement. The shorter the impulse response, the less you can trust the low-frequency result from your FFT. One reason for this is that, when you do an FFT, it uses a “slice” of time to convert the signal into a frequency response. In order to be able to measure a given frequency accurately, the FFT math needs at least one full cycle within the slice of time. Take a look at Figure 6, below.
As you can see in that plot, if the slice of time that we’re looking at is 20 ms long, there is enough time to “see” two complete cycles of a 100 Hz sine tone (in blue). However, 20 ms is not long enough to see even one half of a cycle of a 20 Hz sine tone (in red).
However, there is something else to worry about – a less-well-known relationship between the level and extension of the low-frequency content of the device under test and the impulse response length. (Actually, these two issues are basically the same thing – we’re just playing with how low is “low”…)
Let’s start be inventing a loudspeaker that has a perfectly flat on-axis magnitude response but a low-frequency limitation with a roll-off at 10 Hz. I’ve simulated this very unrealistic loudspeaker by building a signal processing flow as shown in Figure 7.
If we were to do an impulse response measurement of that system, it would look like the plot in Figure 8, below.
Figure 9, above shows a closeup of what happens just after the impulse. Notice that the signal drops below 0, then swings back up, then negative again. In fact, this keeps happening – the signal goes positive, negative, positive, negative – theoretically for an infinite amount of time – it never stops. (This is why the filters that I used to make this high pass are called “IIR” filters or “Infinite Impulse Response” filters.)
The problem is that this “ringing” in time (to infinity) is very small. However, it’s more easily visible if we plot it on a logarithmic scale, as shown below in Figure 10.
As you can see there, after 1 second (1000 ms) the oscillation caused by the filtering has dropped by about 400 dB relative to the initial impulse (that means it has a level of about 0.000 000 000 000 000 000 01 if the initial impulse has a value of 1). This is very small – but it exists. This means that, if we “cut off” the impulse to measure its frequency response, we’ll be cutting off some of the signal (the oscillation) and therefore getting some error in the conversion to frequency. The question then is: how much error is generated when we shorten the impulse length?
We won’t do an analysis of how to answer this question – I’ll just give some examples. Let’s take the total impulse response shown in Figure 6 and cut it to different lengths – 10, 15, 20, 25, 30 and 1000 ms. For each of those versions, I’ll take an FFT and look at the resulting magnitude response. These are shown below in Figure 11.
Figure 11: The magnitude responses resulting from taking an FFT of a shortened portion of a single impulse response plotted in Figure 8.
We’ll assume that the light blue curve in Figure 9 is the “reference” since, although it has some error due to the fact that the impulse response is “only” one second long, that error is very small. You can see in the dark blue curve that, by doing an FFT on only the first 10 ms of the total impulse response, we get a strange behaviour in the result. The first is that we’ve lost a lot in the low frequency region (notice that the dark blue curve is below the light blue curve at 10 Hz). We also see a strange bump at about 70 Hz – which is the beginning of a “ripple” in the magnitude response that goes all the way up into the high frequency region.
The amount of error that we get – and the specific details of how wrong it is – are dependent on the length of the portion of the impulse response that we use.
If we plot this as an error – how wrong is each of the curves relative to our reference, the result looks like Figure 12.
So what?
As you can see there, using a shorted impulse response produces an error in our measurement when the signal has a significant low frequency output. However, as we said above, we shorten the impulse response to delete the early reflections from the walls of The Cube in our measurement to make it “pseudo-anechoic”. This means, therefore, that we must have some error in our measurement. In fact, this is true – we do have some error in our measurement – but the error is smaller than it would have been if the room had been smaller. A bigger room means that we can have a longer impulse response which, in turn, means that we have a more accurate magnitude response measurement.
“So why not use an anechoic chamber and not mess around with this ‘pseudo-anechoic’ stuff?” I hear you cry… This is a good idea, in theory – however, in practice, the problem that we see above is caused by the fact that the loudspeaker has a low-frequency output. Making a room anechoic at a very low frequency (say, 10 Hz) would be very expensive AND it would have to be VERY big (because the absorptive wedges on the walls would have to be VERY deep – a good rule of thumb is that the wedges should be 1/4 of the wavelength of the lowest frequency you’re trying to absorb, and a 10 Hz wave has a wavelength of 34.4 m, so you’d need wedges about 8.6 m deep on all surfaces… This would therefore be a very big room…)
Appendix 1 – Tricks
Of course, there are some tricks that can be played to make the room seem bigger than it is. One trick that we use is to do our low-frequency measurements in the “near field” which is much closer than 3 m from the loudspeaker, as is shown in Figure 13 below. The advantage of doing this is that it makes the direct sound MUCH louder than the wall reflections (in addition to making the difference in their time of arrival at the microphone slightly longer) which reduces their impact on the measurement. The problem with doing near-field measurements is that you are very sensitive to distance – and you typically have to assume that the loudspeaker is radiating omnidirectional – but this is a fairly safe assumption in most cases.
Appendix 2 – Windowing
Those of you with some experience with FFT’s may have heard of something called a windowing function which is just a fact way to slice up the impulse response. Instead of either letting signal through or not, we can choose to “fade out” the impulse response more gradually. This changes the error that we’ll get, but we’ll still get an error, as can be seen below.
So, as you can see with all of those, the error is different for each windowing function and impulse response length – but there’s no “magic bullet” here that makes the problems go away. If you have a loudspeaker with low-frequency output, then you need a longer impulse response to see what it’s doing, even in the higher frequencies.