Category: audio
Any port in a storm?
So, you want to build a loudspeaker…
One of the questions you’ll probably be asking yourself is whether you want to build a ported loudspeaker (sometimes called a “bass reflex” loudspeaker) or one with a sealed enclosure. If you want to know the general reasons why most people think that you should choose one or the other, go somewhere else for information – or maybe come back here later (maybe I’ll talk about it in a later posting).
For this posting, I want to look at a couple of things that I haven’t seen elsewhere – mostly because it helps me to understand the difference between ported and sealed loudspeaker enclosures a little better.
Let’s take a loudspeaker driver and put it in a box. For the purposes of this discussion, we’ll simulate a 10″ driver with mostly-real Thiele-Small parameters in a simulated sealed box. The box has a volume, but we’ll leave out any possible internal modes to keep things simple for now. We’ll also ignore additional effects such as diffraction – we’re just looking at the how the enclosure’s volume and the port dimensions affect the response of the system.
If we sweep a sine wave into the driver, keeping the voltage constant, and we measure the sound pressure level in front of the driver, we’ll see that the total system (the loudspeaker in a sealed box) acts as a minimum phase, second-order high pass filter. Therefore it has a rising slope of 12 dB/octave in the low end. The Q of that high-pass filter will be dependent on the relationship of the driver’s parameters and the size of the box.
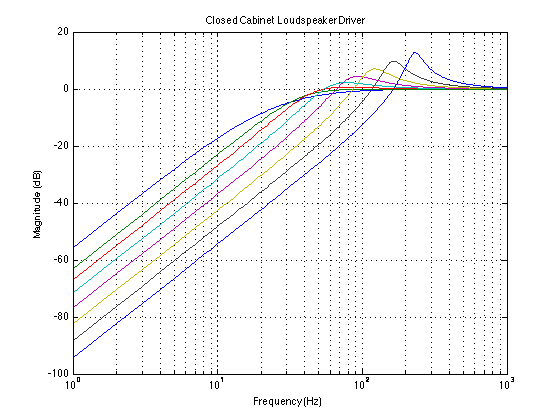
In the plots above, you can see the results on the magnitude response of changing the enclosure volume. The blue curve on the far left is the response you’d get from putting the driver in an infinite baffle (actually, I simulated an enclosure of about a cubic kilometre or so… So not quite infinite, but pretty big for a woofer cabinet…). Notice that it has the highest output at the lowest frequency, but you don’t get as much output around the knee as you do with the other curves. As the enclosure volume is made smaller (The green curve is 1000 litres, and each curve after that, moving left to right, is for a volume of one-half the previous one, so, 500 l, 250 l, 125 l, 62.5 l, 31.25 l, and 15.625 l. Remember – the driver that we’re simulating here isn’t real, so don’t worry about the actual volumes – we’re just worried about the differences in magnitude response as the volumes get smaller.)
You can see in the plots that, by making the volume behind the driver smaller, we do a couple of things at the same time.
- One is that, the smaller the enclosure, the higher the cutoff frequency of the resulting high pass filter. This is because the “spring” supplied by the air in the enclosure gets stiffer (or less compliant) as the box gets smaller, so it rings at a higher frequency.
- Secondly, you’ll notice that the Q of the high pass filter increases as the enclosure gets smaller. This is because the damping factor of the total system (which is, in turn inversely related to the Q – the lower the damping, the higher the Q) decreases as the spring gets stiffer ( and the compliance goes down), if neither the mass nor the losses in the system change.
Both of these are basically the same as having a series RLC circuit and decreasing the capacitor value. The resonant frequency will go up, and the damping factor will go down.
Now, what happens if we wanted to build a ported loudspeaker instead? For now, let’s just use the same loudspeaker driver, a 1000 litre enclosure and we’ll add a port. We’re keeping it simple, so we will just add the port as a pipe sitting outside the enclosure so it doesn’t take away from the enclosure’s volume. Also we will not include the port’s volume as part of the enclosure volume. Also, because this isn’t the real world, we’ll make the port’s output in the same physical location as the loudspeaker driver to avoid any problems with propagation delay and interference at the microphone location.

The above plots show the result of this imaginary ported box with different port lengths, keeping all other parameters constant. I’ve made the losses in the port low so that the port has a bigger contribution to the total magnitude response, and therefore is easier to see. Remember – we’re not simulating the real world – we’re intentionally making the simulation produce curves that show patterns to better understand what’s going on. The ports that I’ve simulated are 10 cm in diameter, and have a length of (again from left-to-right) 1.6 m, 800 cm, 400 cm, 200 cm, 100 cm, 50 cm, 25 cm, and 12.5 cm.
What can we see in these plots?
- Firstly, you can see that the slope of the high pass filter is now steeper than it was with the closed cabinet. This is because a ported loudspeaker enclosure results in a fourth-order high-pass system, so we have a slope of 24 dB/octave. This means that, in the very low end, we have a LOT less output from the ported system than the sealed system.
- Secondly, you can see that, in this case, changing the port length has an puts a bump in the output’s magnitude response around a frequency that is dependent on the port length. The longer the port, the lower the centre frequency of the bump. This isn’t a surprise, since making the port longer lowers the resonant frequency of the Helmholtz resonator. In real life, the bump probably wouldn’t be as prominent – I made it obvious by simulating a port with very low losses (Those losses are the result of things like turbulence around the ends of the port and friction where the air “plug” in the port is rubbing against the sides of the port and the energy is converted to heat.)
- Thirdly, you will see that the cutoff frequency of the system doesn’t change as much as it did when I was changing the volume of the sealed enclosure.
So, how do these systems compare? You’ll often hear people say “I chose to make a bass reflex loudspeaker so that I would get more bass out of the system.” The question is, does this sentence make sense? Is this really a good reason to choose a ported enclosure over a sealed one when you’re building a loudspeaker? Let’s look at what magical wonders adding a port had brought to our pretend loudspeaker…

The above plots show the difference in the output of the systems, showing the relative outputs of the ported systems (the colours are arranged to be the same as the ones in the previous plot so you know which port is which length) compared with the same enclosure without a port (in other words, the green curve from the top plot). Basically, all I’ve done here is subtracted the green curve from the top plot from all the curves in the second plot. If the result is 0 dB (as it is in the high frequency region for all of the curves, then this means that the two systems have the same output. If the value for a given frequency is positive, then this means that the ported system is louder than the sealed system. If the value is negative, then it means that the ported system is quieter by that amount.
As can be seen in that plot, there is a frequency region for all ported systems where you get more output for the same voltage. In the high end, both systems give the same output (because that’s so far above the port resonance that it’s basically not a part of the system, so they both behave the same way). In the low end, the ported system gives much less output because it’s a 4th-order high pass instead of a 2nd-order high pass like the sealed enclosure system.
So far, we can see that a ported system does appear to give you more bass for the same input voltage, assuming that you’ve tuned the port to give you more output in a band that you call bass – however, below that band, you get less. So you might be “robbing Peter to pay Paul” – which might not necessarily be a good idea.
Some people (who might know a little more about what they’re talking about than the last people I mentioned) say “I’m going to build a bass reflex loudspeaker instead of a sealed system to reduce distortion in the driver at the port resonance.” Now why on earth would they say that? Well, a little more digging (not much more digging, admittedly) will turn up an extra little piece of information: the driver moves less at frequencies around the port resonance. For example, at the resonant frequency of the port, the Helmholtz resonator acts against the driver, pushing it out when it tries to move in and pulling it in when it tries to move out. As a result, the excursion of the driver drops. In an extreme (non-real-world) case, if there are no losses in the port or the enclosure, then the driver’s excursion would be 0 at the port resonance. The greater the losses, the less this will be true.
So, let’s check out our two systems again, this time, looking at the driver excursion (peak excursion, to be precise) by frequency.

The above plot shows the peak excursion of the driver in the sealed cabinet. The colours correspond directly to the curves in the first plot at the top of the posting so that you can see the kind of magnitude response you get for the excursion. As you can see, in all cases, the excursion of the driver in the high frequency region is nearly 0 mm – the higher we get, the closer we get to 0 mm. You can also see that, in the low end, the excursion levels out. The more level the excursion plot, the closer the slope of the magnitude response is to a “perfect” 12 dB/octave. This is because the sounds pressure only comes from the air moved by the driver, and because the sound pressure level is proportional to the acceleration of the driver. As the frequency drops and the excursion stays the same, the acceleration drops by 12 dB per halving of frequency because it’s the derivative of the velocity which drops by 6 dB per halving of frequency, because it’s the derivative of the excursion in time.
Of course, if your driver can’t handle the excursions we see here (for example, the one I’m using for this simulation can only move 8 mm before it starts to get unhappy) then you might have something to worry about here. How you deal with that problem, however, is your problem.
So, what would the excursion look like for the same driver in a ported cabinet? Let’s have a look!
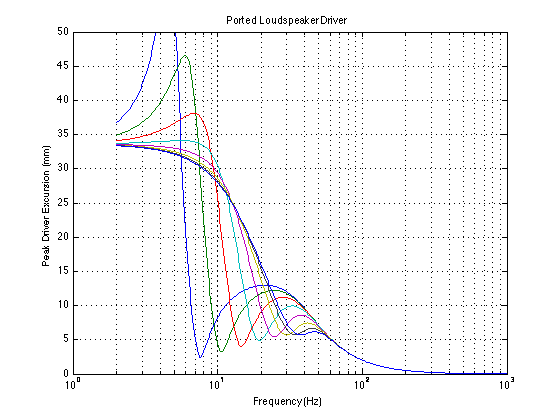
The plot shown above has the peak excursion curves for the same driver in the ported cabinet for the port lengths listed high above… As you can see, starting at the top end, the excursion of the driver is nearly 0 mm, just as in the case of the sealed cabinet. As the frequency drops, the excursion starts to increase. However, then something weird happens. Going lower in frequency, we can see that the driver excursion levels out and starts to drop, with a minimum value at the resonance of the port. If you’re very attentive, you’ll notice that this frequency isn’t exactly the same as the frequency of the bump in the total system’s magnitude response. That’s not a big surprise, since there is some other frequency (in this weird, non-real-life system) where the summed outputs of the driver and port give you more output than they do at the port resonance (actual results may vary). Anyway, going below the port resonance, you can see that the excursion of the driver really takes off and becomes much greater than it was with the sealed system. That’s because there’s nothing there to stop it. At frequencies that are much lower than the port resonance, the system behaves as if the driver wasn’t in a box at all, so it’s free to move as far as it wants to go. (remember that our non-real-life system isn’t limited by things like the maximum excursion of the suspension… The values in the plot show the excursion that the driver “wants” to hit – it’s just held back by real life.)
So, you may be asking yourself a question at this point: “Why is it that, at very low frequencies, the driver’s excursion is much higher in the ported system than in the sealed system, but you get less output?” Good question! The reason is that, at frequencies far below port resonance, you get almost as much output from the port as the driver. The only problem is that the port is just delivering the pressure at the back of the driver to the outside world. So, when the front of the driver goes positive, the back of the driver (and therefore the port) goes negative, and the two cancel each other at the listening position. Putting the port opening at the back of the loudspeaker won’t help much. It will just make the propagation distance a little longer, therefore a little later, but they’ll still cancel each other. This is why the total output of the ported system drops faster as you go lower in frequency – the lower you go, the more the driver and the port cancel each other. They’re both working really hard (and therefore, so is your amplifier), but you get next-to-nothing.
However, let’s back up a bit. There is that issue of the lower driver excursion around the port resonance. This is true. So, if you have a loudspeaker driver that doesn’t like excursion (maybe, say, it distorts when it moves to far) in a particular frequency band, then maybe a port could alleviate the problem. However, beware of frequencies below! Danger danger! (In other words, you might want to put a high pass filter in your system to keep things running smoothly below the port resonance…)

A couple of plots ago, we did some subtraction to compare the magnitude responses of the ported systems to a sealed system. Let’s do the same for the excursion plots. The above figure shows the difference between the peak excursion of the driver in the ported systems, and that of the driver in a sealed enclosure of the same volume. Negative values mean that the ported cabinet driver moves less than the sealed cabinet one. Positive values mean that the ported cabinet driver moves further than the sealed cabinet one.
As you can see in those curves, in the high frequencies, the driver will have the same excursion in both cases. Secondly, there is some region in all cases where the driver moves less in a ported system than in a sealed cabinet of the same volume. At low frequencies, the ported cabinet driver moves further than the sealed cabinet equivalent (yet has less total output, remember!). An interesting detail to note here is to look carefully at this plot with the magnitude difference plot. For example, take a look at the left-most blue curve. The ported system driver has a lower (or equal) excursion than the sealed system driver from about 6.5 Hz and up. Looking at the magnitude response difference curve for the same system, we can see that we get about 6 or 7 dB more output from the ported system at 6.5 Hz, with less and less benefit as we go higher in frequency. Below 6.5 Hz, although we get more output from the ported system for about an octave, it comes at the cost of a much greater excursion, which would probably not be good for our driver.
So what?
Okay, let’s be honest here. I’ve made two very simulated systems, and only changed one variable in each system to see what happens. And, I can absolutely guarantee that (1) no loudspeaker driver in the world has the parameters of the one I’ve simulated and (2) if you built the system I’ve simulated, it wouldn’t behave as I’ve shown here. This is a very isolated, idealised simulation, intentionally designed to make the changes I was making obvious. However, the issues that I’ve made obvious are basically true – I’ve just done a little exaggeration…
What’s the moral of the story? Well, I’m not really sure of all of them. One moral is certainly “sticking a port on a loudspeaker enclosure is not a free ticket to more bass”. Another moral is “people who use ports to reduce driver excursion might not know what they’re talking about”. Probably the most important moral is “don’t trust everything you read” – even the stuff you read here.
Post Script
If you REALLY want to learn this stuff correctly, go read the following:
Closed Box Loudspeaker Systems – Part 1: Analysis
Closed Box Loudspeaker Systems – Part 2: Synthesis
Vented Box Loudspeaker Systems – Part 1: Small Signal Analysis
Vented Box Loudspeaker Systems – Part 2: Large Signal Analysis
Vented Box Loudspeaker Systems – Part 3: Synthesis
Vented Box Loudspeaker Systems – Part 4: Appendices
When you’re done with those, please explain them to me.
It’s impossible to build a good loudspeaker. Part 1: Crossovers
So, you want to build a loudspeaker…
One of the first things you’ll find out is that, if you’re building a loudspeaker with moving coil drivers, and unless you want a loudspeaker with very limited capabilities, you’ll probably need to use more than one driver. Starting small, you’ll at least need a bigger driver to produce the lower frequencies and a smaller driver to produce the higher ones. No surprise so far – many people lead meaningful lives with just a tweeter and a woofer.
However, you’ll probably need to ensure that the tweeter doesn’t get too much signal at low frequencies, and the woofer doesn’t get too many highs. In order to do this, you’ll need a crossover. Still no surprises. Most people who build a loudspeaker already know that they’ll need a crossover to keep their drivers happier.
Now for some new stuff – at least for some people. When you make a crossover, you must remember to keep the driver’s characteristics in mind. You can’t just slap a high pass filter on the tweeter and a low pass filter on the woofer and expect things to work. The tweeter is already behaving as a high pass filter all by itself. If the characteristics of the tweeter’s inherent high pass are what you want, then you don’t want to duplicate that filter in the electronics. So, design your filters wisely. I will probably come back to some examples of this some time in a future posting.
However, that is not the topic for today. For today, we will assume that we are building a loudspeaker using two very special drivers. They are:
- infinitely small
- have bandwidths that go from DC to infinity
- have “perfect” impulse responses
- and therefore have completely flat phase responses
In other words, we will pretend that each of our drivers is a perfect point source. We’ll also assume that they are not mounted on a baffle (a fancy way of saying “on the front of a box” – usually…). Instead, they’re just floating in space, arbitrarily 25 cm apart (one directly above the other). We’ll arbitrarily make the crossover frequency 500 Hz. Finally, let’s say that we’re arbitrarily 2 m away from the loudspeaker.
The reason for all of these assumptions is that, for the purposes of this posting, we’re only interested in the effects of the crossover on the signal, so I’m making everything else in the system either perfect or non-existent. Of course, this has nothing to do with the real world, but I don’t really care today.
So, if you’ve done a little research, you’ll know that there are a plethora of options to chose from when it comes to crossovers. I’ll assume that we’re building an active loudspeaker with a DSP so we can do whatever we want.
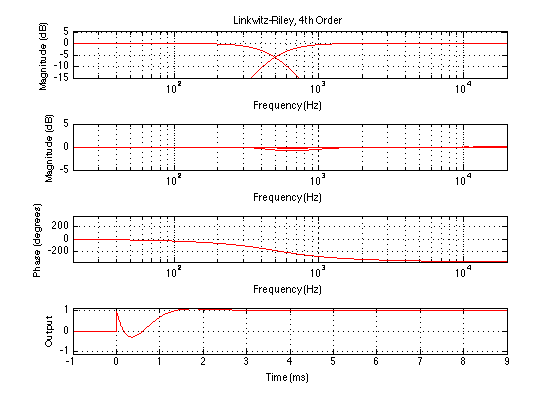
Linkwitz Riley, 4th Order
Let’s start with Old Faithful: a 4th-order Linkwitz-Riley crossover. This is implemented by putting two 12 dB/oct Butterworth filters in series, each with a cutoff frequency equal to the intended crossover frequency. (If you’re using biquads, set your Q to 1/sqrt(2) on each filter). The total low pass section will have a gain of -6.02 dB at the crossover frequency (so will the total high pass section). Since the two sections are 360° out of phase with each other at all frequencies, they’ll add up to give you a total of 0 dB when they sum together at any frequency. However, you must remember that the filter sections used in the crossover have an effect on the phase response of the re-combined signal. As a result, when the two are added back together (at the listening position) the total will also have a modified phase response – even when you are on-axis to the loudspeakers, (and equidistant to the two loudspeaker drivers).
It is also important to remember that the phase relationship of the two sections (coming from the tweeter and the woofer) is only correct when those two drivers are the same distance from the listener. If the tweeter is a little closer to you (say, because the tweeter is on top and you stood up) then its signal will arrive too early relative to the woofer’s and the phase relationship of the two signals will be screwed up, resulting in an incorrect summing of the two signals.
How much the total is screwed up depends on a bunch of factors including
- the relative phase responses of the filters in the crossover
- the phase responses of the drivers (we’re assuming for this posting that this is not an issue, remember?)
- the deviation in those phase responses caused by the mis-alignment of distances to the drivers
The result of this is a deviation in the vertical off-axis response of the loudspeaker. How bad is this? Let’s look!
This figure shows 4 plots. The top one shows the magnitude responses of the two individual sections. As you can see, the crossover frequency is 1 kHz, and both sections are 6 dB down at that frequency.
The second plot shows the total magnitude responses at 5 different vertical angles of incidence to the loudspeaker: -30°, -15°, 0°, 15°, and 30°. So, we’re going from below the loudspeaker to above the loudspeaker. It’s not obvious which plot is for which angle because, for the purposes of this discussion, it doesn’t matter. I’m only interested in talking about how different the loudspeaker sounds at different angles – not the specifics of how it sounds different.
The third plot shows the total phase response of the system, at a position that is on axis to the loudspeaker (and therefore equidistant to both drivers). As you can see there, a perfect 2-way loudspeaker with a 4th order Linkwitz-Riley crossover behaves as a 4th-order allpass filter. In other words, at low frequencies, the output is in phase with the input. At the crossover frequency, the output is 180° out of phase with the input. At high frequencies, the output is 360° out of phase with the input.
The fourth plot shows the step response of the total system, at a position that is on axis to the loudspeaker (and therefore equidistant to both drivers). As you can see there, a perfect 2-way loudspeaker with a 4th order Linkwitz-Riley crossover does not give you a “perfect” step response – it can’t, since it acts an allpass filter. The weird shape you see there is cause by the fact that the high frequencies are not “in phase” with the low frequencies. (I know, I know… different frequencies cannot be “in phase”.) Since different frequencies are delayed differently by the total system, they do not add up correctly in the time domain. Thus, although the total output in terms of magnitude is flat (hence the flat on-axis frrequency response) the time response will be weird.
Looking in detail at the step response plot, you can see that it takes about 1.5 ms for the total output to settle to a value of 1. The actual time that it takes is dependent on the crossover frequency. The lower the frequency, the longer it will take. It’s the shape of the step response that’s determined by the crossover’s phase response. What can be seen from the shape is that the high-frequency spike hits first (as we would expect), then the step response drops back to a negative value before heading upwards. It overshoots, peaking at a value of 1.0558 before coming back down, undershooting slightly (to a value of 0.9976) and finally settling at a value of 1. Note that these values won’t change with changes in crossover frequency – they’ll just happen at a different time. The higher the frequency, the faster the response.
Whether or not this modified time response is worth worrying about (i.e. can you hear it) is also outside of the scope of today’s discussion. All we’re going to say for today is that this temporal distortion exists, and it is different for different crossover strategies as we’ll see below.
Linkwitz-Riley 2nd Order
A second possible crossover strategy is to use a 2nd-order Linkwitz Riley. This is similar to a 4th-order, except that instead of putting two 12 dB/octave Butterworth filters in series to make each section, you put two 6 dB/octave Butterworth filters in series.
Since the total filters applied to make the high pass and low pass sections of this crossover are each made with only two first-order filters (instead of two second-order filters), the high pass and low pass sections are only 180 degrees out of phase with each other (at all frequencies). Consequently, in order to get them to add back together without cancelling completely at the crossover frequency, you have to invert the polarity of one of the sections. (We’ll do this to the high pass section, just in case you can hear your woofers pulling when they ought to push when a kick drum hits). On the plus side, since they’re 180 degrees out of phase at all frequencies, if you DO flip the polarity of your high pass section, they’ll add back together (on axis) to give you a flat magnitude response.
As you can see in the above plots, the slopes of the high pass and low pass sections in this crossover type are more gentle than in the 4th order Linkwitz Riley. This should be obvious, since they have a lower order. In the second plot, you can see that, on-axis, the magnitude response is flat, just as we would expect. However, there are implications on the off-axis response. The deviation from “flat” is greater with the 2nd-order LR than it is with the 4th-order version. Not by much, admittedly, but it is greater. So, if you’re concerned about deviations in your off-axis response in the vertical plane, you might prefer the 4th-order LR over the 2nd-order variant.
If, however, you lay awake at night worring about phase response (you know who you are – yes – I’m talking you YOU) then you might prefer the 2nd-order Linkwitz Riley, since, as you can see in the third plot, the total output is only 180° out of phase with its input in the worst case – only half that of the 4th-order variant. On the other hand, since it’s 180° out of phase, that means that a high voltage going into the system (at high frequencies) will come out as a low pressure. So, if you’re the kind of person who lays awake at night worrying about “absolute phase” (you know who you are – yes – I’m talking to YOU) then this might not be your first choice.
Finally, take a look at the step response in the final plot. You’ll notice immediately that the high frequencies are 180° out iof phase, since the initial transient of the step goes down instead of up. You’ll also notice that the step “recovers” to a value of 1 a little faster than the 4th order Linkwitz Riley. Note that, a 2nd order LR, doesn’t have the overshoot that we saw in the 4th order version.
Butterworth, 12 db/octave
Possibly the most common passive crossover type (and therefore, possibly the most common crossover type, period!) is the 12 dB/octave Butterworth crossover. This is made by using a 2nd-order Butterworth filter for each section (the high pass and the low pass).
You’ll notice in the top plot that this means that the filter sections are only 3 dB down at the crossover frequency. This has some implications on the on-axis response. Since the two filter sections are 180° out of phase with each other (at all frequencies – just like the 2nd-order LR crossover) then we have to flip the polarity of one of the sections (the high-pass section again, for all the same reasons) to prevent them from cancelling each other at the crossover frequency when they’re added back together. However, now we have a problem. Since the two sections are in-phase (due to the 180° phase shift plus the polarity flip) and since they’re only 3 dB down at the crossover frequency, when they get added back together, you get more out than you put into the system. This can be seen in the second plot, where the total magnitude response has a bump at the crossover frequency – even when on-axis.
Of course, a 3 dB bump in the magnitude response will be audible, at the very least as a change in timbre (3 dB is, after all, twice the power). We can also see that there is a small, but visible change in the overall magnitude response as you change the vertical angle to the listener.
The third plot shows that a 12 dB/Octave Butterworth crossover, when all other issues are ignored, acts as a 2nd-order allpass filter with a worst-case phase distortion of 180°.
Finally, the fourth plot shows that its step response is similar, but not identical to, the 2nd-order LR crossover. The initial transient goes negative because we have inverted the polarity of the high pass section. Unlike the 2nd-order LR (but similar to the 4th-order LR), however, there is an overshoot and undershoot before the response settles at a value of 1. That overshoot reaches a maximum of 1.1340, and the subsequent undershoot goes down to 0.9942.
Butterworth, 18 db/oct
Constant Voltage, (using a Butterworth, 18 db/oct high pass)
Never trust a THD+N measurement: v2
In the last post, I talked about why a THD+N measurement is useless if you don’t know about the type of distortion that you’re measuring. Let’s now talk about another reason why it’s useless in isolation.
Once again, let’s assume that we’re doing a THD+N measurement the old-fahsioned way where we put a sine wave into a device, and apply a notch filter to the output at the same frequency of the sine wave and find the ratio of the level of the sine wave to the output of the notch filter.
This time, instead of taking a signal and distorting it, I’ll do some additive synthesis. In other words, I’ll build a final signal that contains four components (although they’re not entirely independent…):
- a “signal” consisting of a 100 Hz sine wave which we’ll call “the fundamental”
- sine tones at frequencies that are multiples of the fundamental frequency (in other words, they are harmonically related to the fundamental).
- sine tones at frequencies that are not multiples of the fundamental frequency (in other words, they are not harmonically related to the fundamental).
- wide-band noise
Let’s start by listening to the original 100 Hz sine wave with a level of -10 dB FS without any other additional components. If you hear any distortion or noise, then this is a problem in your playback system (unless your system is so good that you can hear the quantisation error caused by the fact that I didn’t dither the signal).
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
Now let’s add noise. I’ve added noise with a white spectrum and a level such that a THD+N measurement will tell us that we have 10% THD+N (relative to the level of the 100 Hz sine tone signal). In other words, I have a sine wave with a level of -10 dB FS and I have added white noise with a long-term RMS level of -30 dB FS.
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
The punch line!
Each of the six signals I’ve presented above in Versions 2 through 7 (inclusive) is a “distorted” version of the original 100 Hz sine tone in Version 1. Each of those six signals will have a measurable THD+N of 10%. However, it is quite obvious that they have very different spectral patterns, and therefore they sound quite different.
This isn’t really revolutionary – it’s jut another reminder that a THD value, in the absence of any other information, isn’t terribly useful – or at least, it doesn’t tell you much about how the signal sounds.
Never trust a THD+N measurement: v1
Caveat: This is basically a geek version of a cover tune. The point that I make here was one that I originally heard someone else present at an AES convention years ago. However, since I haven’t heard anyone tell this story since, I’ve written it here.
Let’s build two black boxes, each of which creates a measurable distortion. We’ll call them Box “A” and Box “B”.
Box “A” has a measured THD+N of 20%. Box “B” has a measured THD+N of 2%. We’ll be using the old-fashioned way of measuring THD+N where we put a sine wave into the device, and apply a notch filter to the output at the same frequency of the sine wave and find the ratio of the level of the sine wave to the output of the notch filter.
Let’s put a 500 Hz sine wave into the boxes and listen to the output. The original sine wave sounds like the following:
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
The sine wave at the output of Box “A” (with a THD+N of 20%) sounds like the following:
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
The sine wave at the output of Box “B” (with a THD+N of 2%) sounds like the following:
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
So far so good. There should be no surprises yet.
Now let’s put a recording of something that I listen to all the time (my own voice) into the same black boxes to see what happens.
We’ll start with the original recording (this is just a file that I happened to have on my hard drive for testing imaging – ignore the fact that it talks about coming from the left channel only – your computer will probably play it as a mono file out both channels – this is irrelevant to the discussion):
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
Now let’s listen to how that recording sounds at the output of Box “A” (with a measured THD+N of 20%)
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
As you’ll hear, there is no audible distortion on the sound file, despite the fact that it has gone through a box that generates a distortion that we measured to be 20%.
Now let’s listen to how the original recording sounds at the output of Box “B” (with a measured THD+N of 2%)
To play the media you will need to either update your browser to a recent version or update your Flash plugin.
As you will probably hear in that last sound file, the Box “B” – the one with “only” 2% distortion sounds MUCH worse than either the original sound file or the output of Box “A” which should have much more audible distortion.
So, the question is “why?”
Let’s look at the waveforms to see what’s going on here.
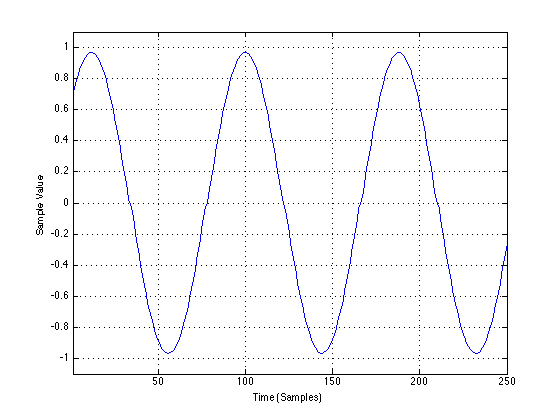
The original sine wave looks like the following:
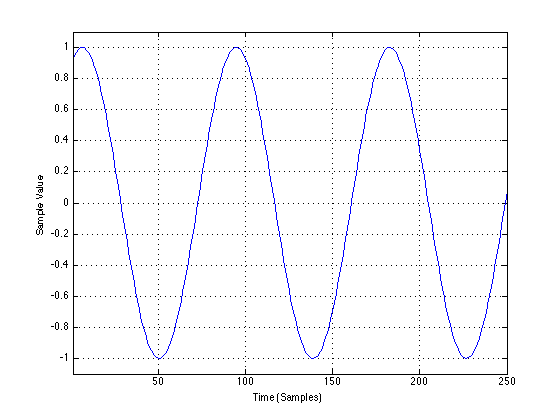
After that sine wave has gone through Box “A”, the output looks like the following:
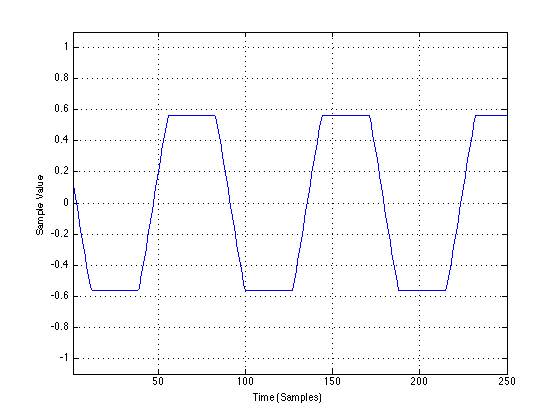
As you can see, I’ve created Box “A” to generate its distortion by clipping the signal at a limits of -0.5 and 0.5.
The output of Box “B” when fed with the same sine wave looks like the following:
If we zoom in on that plot, it looks like the following:
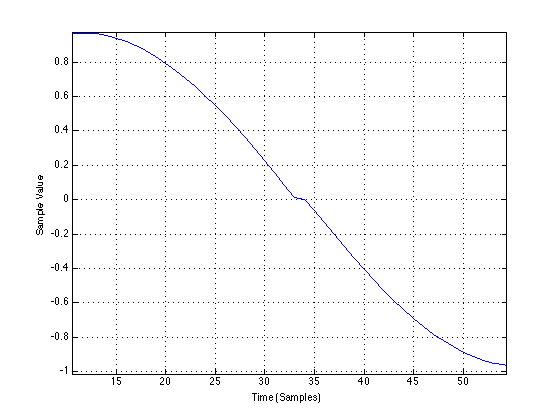
So, as you can see, I’ve made Box “B” to generate a zero-crossing distortion – but a pretty small one.
The reason the THD+N of Box “A” is 20% and that of Box “B” is only 2% is not just because the “damage” done to the signal is bigger with Box “A”. It’s also caused by where the damage is done. This might not make sense, so let’s look at the signals a little differently.
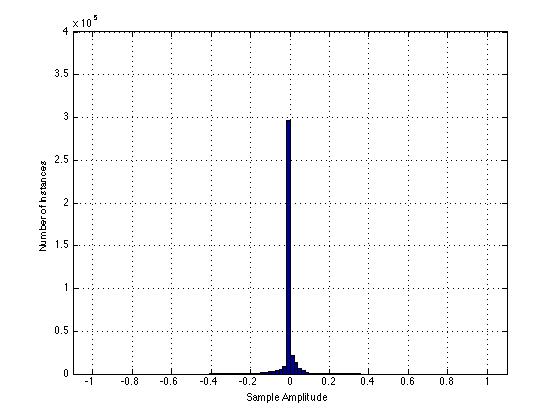
Let’s do a histogram of the original sine wave. This tells us how often the sample values are a given value. This is shown below in the following plot.
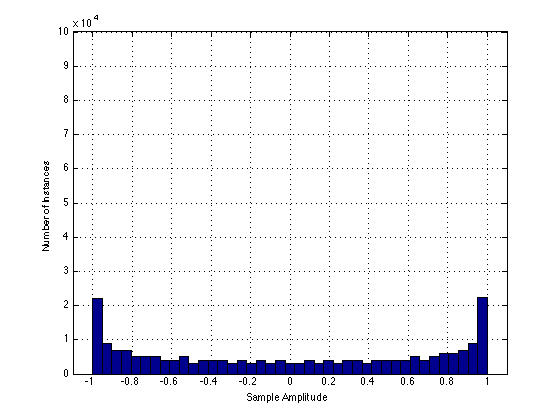
This histogram shows that the sample values in the original sine wave are usually near -1 and +1, and rarely around 0.
Now let’s look at a histogram of the output of Box “A” – the distorted sine wave with 20% THD+N. It looks like the following:
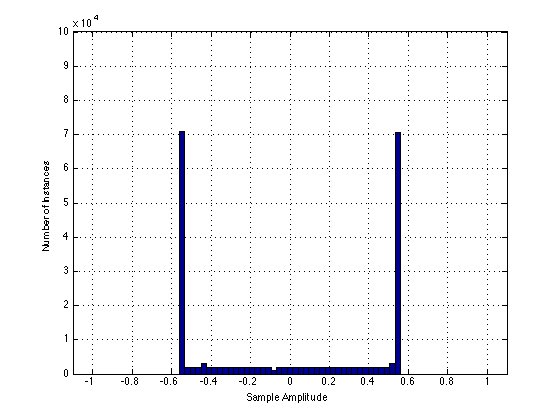
As can be seen in the plot above, the sample values from the original sine wave that were below -0.5 are now all congregated at -0.5, and the values that were above 0.5 are now congregated at 0.5. This is the result of the clipping applied to the signal.
By comparison, the histogram of the output of Box “B” is shown below:
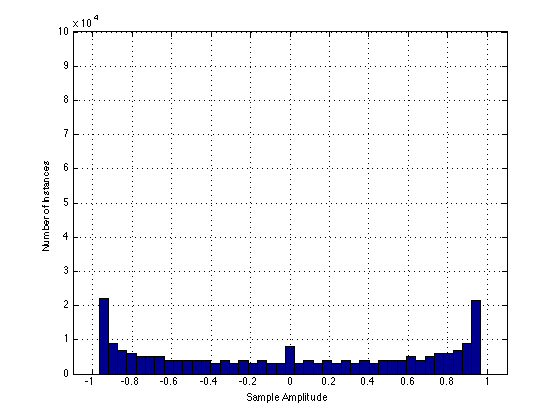
As you can see by comparing these last two plots, the zero crossing distortion of Box “B” results in a histogram that is more similar to the histogram of the original signal than that of the clipping distortion of Box “A”. This is because the zero crossing distortion distorts the signal where the signal rarely is.
Now let’s look at the histograms of the speech signal. Below is a histogram of the original speech recording.
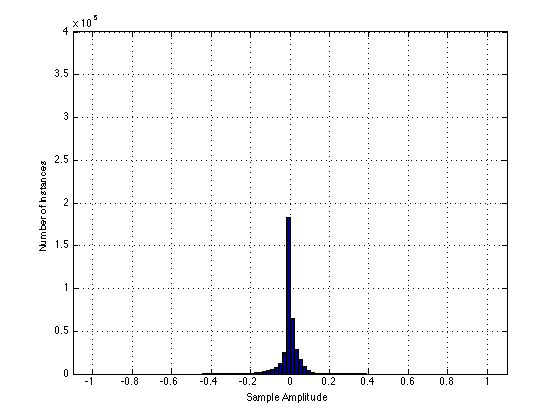
As you can see in this plot, the speech signal is unlike the sine wave in that it is usually at 0, and not at the extreme values of -1 and 1. In addition, you can see that very little, if any, of the signal is below -0.5 or above 0.5 which are the clipping values of Box “A”. Consequently, as you can see below, the histogram of the output of Box “A”, when fed with the speech signal, looks almost the same as the histogram of the original signal, above.
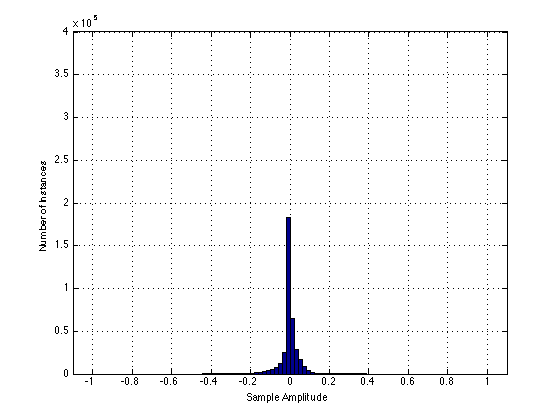
However, the output of Box “B” is different. The histogram of that signal is shown below:
So, as you can see here: the zero crossing distortion is affecting the signal where it is most often, whereas the clipping of Box “A” has no effect on the signal.
The moral of the story
The point that I’ve (hopefully) illustrated here is that the value generated by a THD+N measurement is basically irrelevant when it comes to expressing how a device distorts a normal signal. However, the problem is not with the measurement technique, but the signal that is used in the procedure. We use a sine wave to do a THD+N measurement because that used to be the easy way to do a THD+N measurement back in the old days of signal generators, analogue notch filters, and voltmeters. The problem is that the probability distribution function (PDF) of that sine wave is completely unlike the PDF of a music or speech signal. So, if the distortion of the device affects the signals in the wrong place, then the result of the measurement will not reflect the sound of the device.
the problem with windows
Now, before you start sending me hate mail because you think this posting is a Windows vs. Mac lecture, hold your horses. That’s NOT the kind of windows I’m talking about. This one’s about windowing functions and one (possibly unexpected) effect on the results of the analysis of the impulse response of an allpass filter. So, if you want to debate Windows vs. Mac – go somewhere else. If you think that you can get all riled up over a Blackman Harris window function, read on!
Last week I had to do some frequency-domain analysis of a system that had a small problem with noise in its impulse response measurements. The details of where the noise came from are unimportant. There is only one important thing from the back-story that you need to know – and that is that I was measuring the response of an allpass filter implementation.
So, I did my MLS measurement of the allpass filter and, because I had noise in the impulse response, I chose to use a windowing function to clean up the impulse response’s tail. Now, I know that, by using a windowing function (or a DFT, for that matter), there are consequences that one needs to be aware of. However, the consequence that I stumbled on was a new one for me – although in retrospect, it should not have been.
Here’s a sterilised version of what happened, just in case it’s of use.
Below is a plot showing a (very clean) impulse response of an allpass filter. To be more specific, it’s a 4th order Linkwitz Riley crossover with a crossover frequency of 100 Hz, where I summed the outputs of the high pass and low pass components together to make an output. (We will not discuss why I did it this way, since that information is outside the scope of this discussion.) In addition, I have plotted three windowing functions, a Hann, a Hamming and a Blackman Harris.

Note that the length of the windowing functions is big – 65536 samples to be exact. As you can see in the plot, the ringing of the allpass filter is negligible in this plot by the time we get to the end of the window. This can also be seen below in the next two plots where I’ve shown the impulse response after it has been windowed by the three (actually four, if we include rectangular as a function), scaled in linear and dB FS. (I know, I know, dB FS is an RMS measurement and I plotted this as instantaneous values – sue me.)


So, if you now take those windowed impulse responses and calculate their magnitude and phase responses, you get the plots shown below.

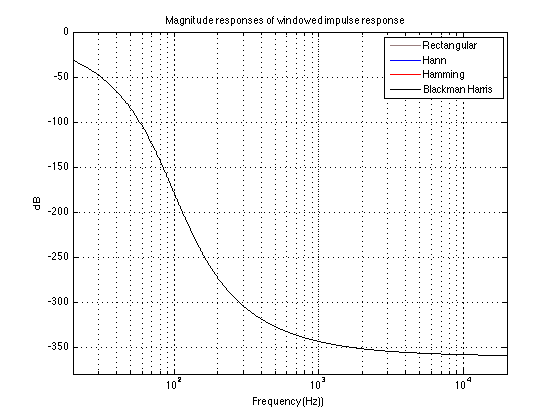
“So what?” I hear you cry. The magnitude responses of the four versions of the windowed impulse response are all identical enough that their plots lie on top of each other. This is also true for their phase responses. “I see what I would expect to see – what are you complaining about?” I hear you cry.
Well, let me tell you. The plots above show the results when you use a 65536-point FFT and a 65536-sample window (okay, okay, DFT – sue me).
Let’s do all that again, but with a 65536-point FFT and a 1024-point window instead (I did this in MATLAB, so it’s zero-padding the impulse responses with the remaining 65536-1024 = 64512 samples.)

Now we can see immediately, that the ringing in the allpass filter’s impulse response hasn’t settled down by the time we get to the end of the window. This can also be seen in the following two plots.

- The result of the windowing functions on the impulse response.

As you can see there, the impulse response itself (aka “Rectangular” windowing) is only about 60 dB below its peak when we reach the end of the window. How does this then affect our magnitude response?
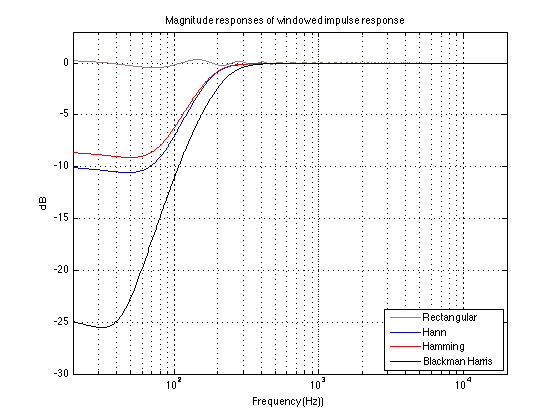
As you can see there, the implications on the rectangular window is a ripple in the low end of the calculated magnitude response. As you can also see there, the result of attenuating the tail of the allpass filter’s impulse response before we unceremoniously cut it off is that we lose low-end in the magnitude response. The more we attenuate in the windowing function, the more low end we lose.
Of course, this also has implications on the phase response of the windowed impulse responses, as is shown below.

The moral of this story is not a new one: beware of the effects of a windowing function on your analysis.
In my personal case, it’s a memorable lesson, since I didn’t get to this conclusion immediately. This is because I was measuring the allpass with different Fc’s – and what I saw in my magnitude response was a shelving response (I was using a Blackman Harris window). When I changed the Fc of the allpass, the shelving response that I saw moved appropriately. So, my conclusion was that there was a problem in my filter that I was measuring. It took some time (too much time!) before I figured out (with the help of some more level-headed friends) that my problem was the window length and my windowing function, not the filter that I was measuring. Won’t make that mistake again for a while…
achieving distance and depth in stereo recordings – one man’s opinion
I had an interesting email from an old recording-engineer friend of mine this week regarding a debate he had with a student concerning the issue of “depth” in recordings (in his specific case, 2-channel stereo recordings done with an ORTF mic configuration). This got me thinking about to a bunch of thoughts I had once-upon-a-time about distance perception, and a newer bunch of thoughts about loudspeaker directivity. Now, those two bunches of thoughts are congealing into a single idea regarding how to achieve (and experience) a reasonable perceived sensation of distance and depth in 2-channel stereo.
To start, some definitions:
- When I say “stereo” I mean “2-channel sound recording”
- “Distance” to a source in a stereo recording is the perceived distance between the listener and the (probably phantom) image.
- “Depth” in a stereo recording is the difference in the perceived distances from the listener to the closest and farthest (probably phantom) images (i.e. the distance to the concert master vs. the distance to the xylophone in a symphony orchestra)
Go to an anechoic chamber with a loudspeaker and a friend. Sit there and close your eyes and get your friend to place the loudspeaker some distance from you. Keep your eyes closed, play some sounds out of the loudspeaker and try to estimate how far away it is. You will be wrong (unless you’re VERY lucky). Why? It’s because, in real life with real sources in real spaces, distance information (in other words, the information that tells you how far away a sound source is) comes mainly from the relationship between the direct sound and the early reflections. If you get the direct sound only, then you get no distance information. Add the early reflections and you can very easily tell how far away it is. This has been proven in lots of “official” listening tests. (For example, go check out this report as a basic starting point).
Anecdote #1: Back in the old days when I was working on my Ph.D. we had an 8-loudspeaker system in the lab – one speaker every 45° in a circle around the listening position. We were trying to build a multichannel room simulator where we were building a sound field, piece by piece – the direct sound and (up to 3rd-order) early reflections had the “correct” panning, delay and gain, and we added a diffuse field to tail in behind it. One of the interesting things that I found with that system was that the simulated distance to the source was easily to achieve with just the 1st-order reflections, but that the precision of that perceived distance was increased as we added 2nd- and 3rd-order reflections. (We didn’t have enough computing power to simulate higher-order reflections at the time. It would be interesting to go back and try again to see what would happen with higher-order stuff now that my Mac has gotten a little faster…) Another interesting thing (although, in retrospect, it shouldn’t surprise anyone) was that the location and the distance to the simulated sound source were also easy to determine without the direct sound being part of the sound field at all. Just the 1st- to 3rd-order reflections by themselves were enough to tell you where things were.
Anecdote #2: I did a recording for Atma once-upon-a-time in a large church in Montreal with a very long reverb time. During the sessions, I sat in the church (no control room), about 20 m from the mic pair. So, when I and the organist discussed what take to do next, we were talking live in the same room – no talkback speakers. During the editing for this disc, I happened to be shuttling around, looking for the beginning of a take – so I’d drop the cursor somewhere on the screen and hit “play” quickly to see where I was. One of the takes ended with the organist asking “did we get it?” and I responded “yup” quickly and loudly. It just so happened that, when I was shuttling around, looking for the right take, I hit “play” at the beginning of the “yup” and then quickly hit “stop”. The interesting thing is that it sounded, for that split second, like I was right next to the microphones – not 20 m away like I knew I was. So, I hit “play” again, and this time didn’t hit stop. This time, I sounded far away. What’s going on? Well, because the church was so big, it was possible to hit the stop button before any of the first reflections came in (save maybe the one off the floor), so it was possible (with a fast enough thumb on the transport buttons of the editing machine) to make the recording of my voice anechoic. The result was that I sounded 0 m away instead of 20 m.
The moral of the stories thus far? In order to deliver a perception of precise distance and depth (even if it’s not accurate…) you need early reflections in the recording, and they have to be panned and delayed appropriately.
Step 3: The delivery
Think back to Step 1. We agreed (or at least I said…) that early reflections tell your brain how far away the sound source is. Now think to a loudspeaker in a listening room.
Case #1: If you have an anechoic room, there are no early reflections, and, regardless of how far away the loudspeakers are, a sound source in the recording without early reflections (i.e. a close-mic’ed vocal) will sound much closer to you than the loudspeakers.
Case #2: If you have a listening room with early reflections, but the loudspeakers are directional such that there is no energy being delivered to the side walls (for example, a dipole with the angles carefully chosen to point the null of the loudspeaker at the point of specular reflection from the side wall), then the result is the same as in Case 1. This time there are no early reflections because of loudspeaker directivity instead of wall absorption, but the effect at the listening position is the same.
Case #3: If you have a listening room with early reflections, and the loudspeakers are omni-directional, then the early reflections from the side walls tell you how far away the loudspeakers are. Therefore, the close-mic’ed vocal track from Case #1 cannot sound any closer than the loudspeakers – your brain is too smart to be told otherwise.
The punchline
So, if you want to achieve precision in the distance and depth of your stereo recordings (whether you’re on the recording end or the playback end) you’re going to need to make sure that you have a reasonable mix of the following:
- Early reflections in the recording itself have to be there, and coming in at the right times with the right gains with the right panning
- Not much energy in the early reflections in your listening room – either by putting some absorption on the walls in the right places, or by having reasonably directional loudspeakers (or both).
x192.org
music videos
squeaker #1
- get a bicycle pump
- hold the nozzle firmly against a fleshy part of your belly
- pump
- watch your two-year-old find this hilariously funny.
- note that the pitch of the squeak can be controlled both by the pump velocity and the nozzle pressure. mastering this takes great practice.