#62 in a series of articles about the technology behind Bang & Olufsen products

Over the past year or so, I’ve had lots of discussions and interviews with lots of people (customers, installers, and journalists) about Bang & Olufsen’s loudspeakers – BeoLab 90 in particular. One of the questions that comes up when the chat gets more technical is whether our loudspeakers use native sampling rates or sampling rate conversion – and why. So, this posting is an attempt to answer this – even if you’re not as geeky as the people who asked the question in the first place.

There are advantages and disadvantages to choosing one of those two strategies – but before we get to talk about some of them, we have to back up and cover some basics about digital audio in general. Feel free to skip this first section if you already know this stuff.

A very quick primer in digital audio

An audio signal in real life is a change in air pressure over time. As the pressure increases above the current barometric pressure, the air molecules are squeezed closer together than normal. If those molecules are sitting in your ear canal, then they will push your eardrum inwards. As the pressure decreases, the molecules move further apart, and your eardrum is pulled outwards. This back-and-forth movement of your eardrum starts a chain reaction that ends with an electrical signal in your brain.

If we take your head out of the way and replace it with a microphone, then it’s the diaphragm of the mic that moves inwards and outwards instead of your eardrum. This causes a chain reaction that results in a change in electrical voltage over time that is analogous to the movement of the diaphragm. In other words, as the diaphragm moves inwards (because the air pressure is higher), the voltage goes higher. As the diaphragm moves outwards (because the air pressure is lower) the voltage goes lower. So, if you were to plot the change in voltage over time, the shape of the plot would be similar to the change in air pressure over time.

We can do different things with that changing voltage – we could send it directly to a loudspeaker (maybe with a little boosting in between) to make a P.A. system for a rock concert. We could send it to a storage device like a little wiggling needle digging a groove in a cylinder made of wax. Or we could measure it repeatedly…

That last one is where we’re headed. Basically speaking, a continuous, analogue (because it’s analogous to the pressure signal) audio signal is converted into a digital audio signal by making instantaneous measurements of it repeatedly, and very quickly. It’s a little bit like the way a movie works: you move your hand and take a movie – the camera takes a bunch of still photographs in such quick succession that, if you play back the photos quickly, it looks like movement to our slow eyes. Of course, I’m leaving out a bunch of details, but that’s the basic concept.

So, a digital audio signal is a series of measurements of an electrical voltage (which was changing over time) that are transmitted or stored as numbers somehow, somewhere.

 

 

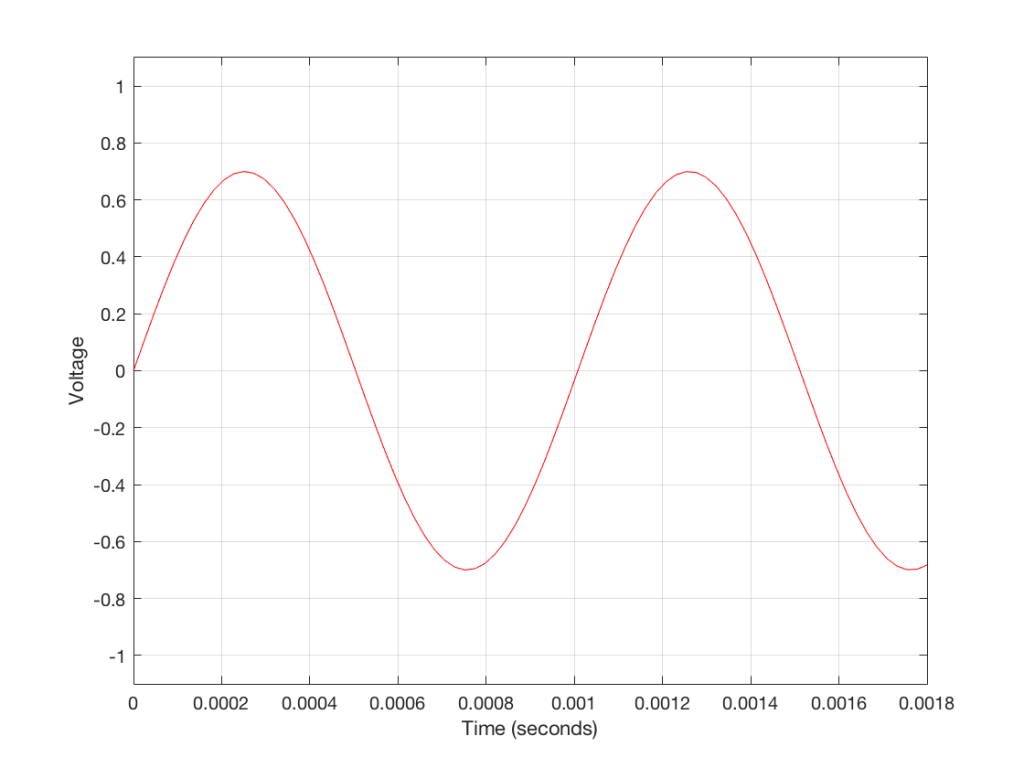
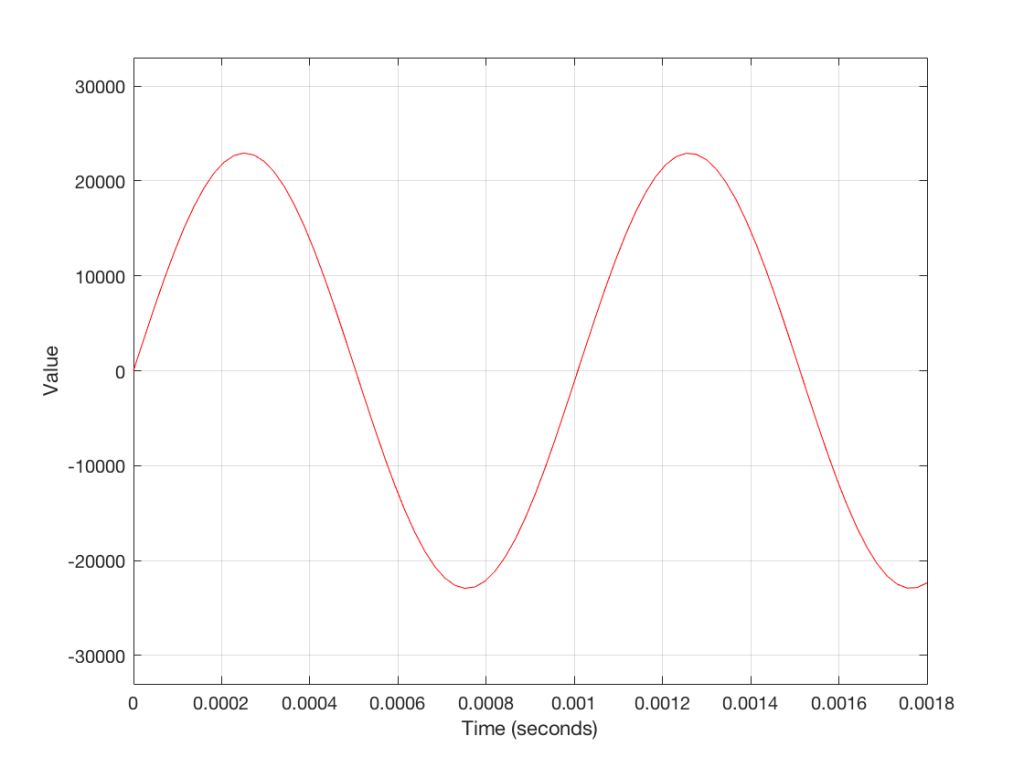
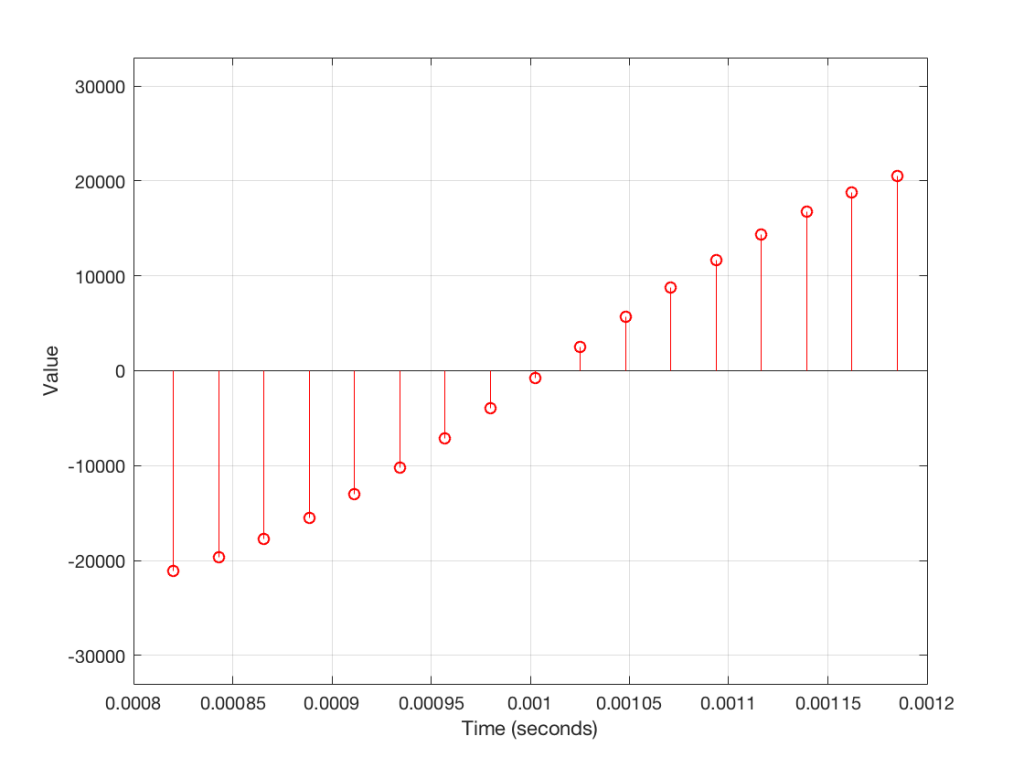
Figure 3 shows a small slice of time from Figure 2, which is, itself a small slice of time that normally is considered to extend infinitely into the past and the future. If we want to get really pedantic about this, I can tell you the actual values represented in the plot in Figure 3. These are as follows:

 

• -21115
• -19634
• -17757
• -15522
• -12975
• -10167
• -7153
• -3996
• -758
• 2495
• 5698
• 8786
• 11697
• 14373
• 16759
• 18807
• 20477

The actual values that I listed there really aren’t important. What is important is the concept that this list of numbers can be used to re-construct the signal. If I take that list and plot them, it would look like Figure 4.

So, in order to transmit or store an audio signal that has been converted from an analogue signal into a digital signal, all I need to do is to transmit or store the numbers in the right order. Then, if I want to play them back (say, out of loudspeaker) I just need to convert the numbers back to voltages in the right order at the right rate (just like a movie is played back at the same frame rate that the photos were take in – otherwise you get things moving too fast or too slowly).

One last piece of information that you’ll need before we move on is that, in a digital audio system, the audio signal can only contain reliable information below the frequency that is one-half of the “sampling rate” (which is the rate at which you are grabbing those measurements of the voltages – each of those measurements is called a “sample”, since it’s taking an instantaneous sample of the current state of the system). It’s just like taking a blood sample or a water sample – you use it as a measurement of one portion of one thing right now. This means that if you want to record and play back audio up to 20,000 Hz (or 20,000 cycles per second – which is what textbooks say that we can hear) you will need to be making more than 40,000 measurements per second. If we use a CD as an example, the sampling rate is 44,100 samples per second – also known as a sampling rate of 44.1 kHz. This is very fast.

Sidebar: Please don’t jump to conclusions about what I have said thus far. I am not saying that “digital audio is perfect” (or even “perfect-er or worse-er than analogue”) or that “this is all you need to understand how digital audio works”. And, if you are the type of person who worships at “The Church of Our Lady of Perpetual Jitter” or “The Temple of Inflationary Bitrates” please don’t email me with abuse. All I’m trying to do here is to set the scene for the discussion to follow. Anyone really interested in how digital audio really works should read the collected writings of Harry Nyquist, Claude Shannon, John Watkinson, Jamie Angus, Stanley Lipshitz, and John Vanderkooy and send them emails instead.  (Also, if you’re one of the people that I just mentioned there, please don’t get mad at me for the deluge of spam you’re about to receive…)

 

Filtering an audio signal

Most loudspeakers contain a filter of some kind. Even in the simplest passive two-way loudspeaker, there is very likely a small circuit called a “crossover” that divides the analogue electrical audio signal so that the low frequencies go to the big driver (the woofer) and the higher frequencies go to the little driver (the tweeter). This circuit contains “filters” that have an input and an output – the output is a modified (or filtered) version of the input. For example, in a low-pass filter, the low frequencies are allowed to pass through it, and the higher frequencies are reduced in level (which makes it useful for sending signals to the woofer).

Once again over-simplifying, this is accomplished in an electrical circuit by playing with something called electrical impedance – a measure of how much the circuit impedes the flow of current to the next device. Some circuits will impede the flow of current if it’s alternating quickly (a high frequency) other circuits might impede the flow of current if it’s alternating slowly (a low frequency). Other circuits will do something else…

It is also possible to filter an audio signal when it is in the digital domain instead. We have the series of numbers (like the one above) and we can send these to a mathematical function which will change the values into other numbers to produce the desired characteristics (like a low-pass filter, for example).

As a simple example, if we take all of the values in the list above, and multiply them by 0.5 before converting them back to voltages, then the output level will be quieter. In other words, we’ve made a volume knob in the digital domain. Of course, it’s not a very good knob, since it’s stuck at one setting… but this isn’t a course in advanced DSP…

If you want to make something more exciting than a volume knob, the typical way of making an audio filter in the digital world is to use delays to mix the signal with delayed copies of itself. This can get very complicated, but let’s make a simple filter to illustrate…

 

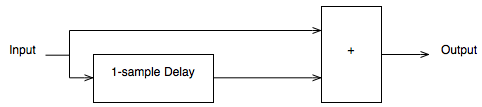
Figure 5 shows a very simple low pass filter for digital audio. Let’s think though what will happen when we send a signal through it.

If you have a very low frequency, then the current sample goes into the input and heads in two directions. Let’s ignore the top path for now and follow the lower path. The sample goes into a delay and comes out on the other side 1 sample later (in the case of a CD, this is 1/44100-th of a second later).  When that sample comes out of the delay, the one that followed it (which is now “now” at the input) meets it at the block on the right with the “+” sign in it. This adds the two samples together and spits out of the result. In other words, the filter above adds the current audio sample to the previous audio sample and delivers the result as the current output.

What will this do to the audio signal?

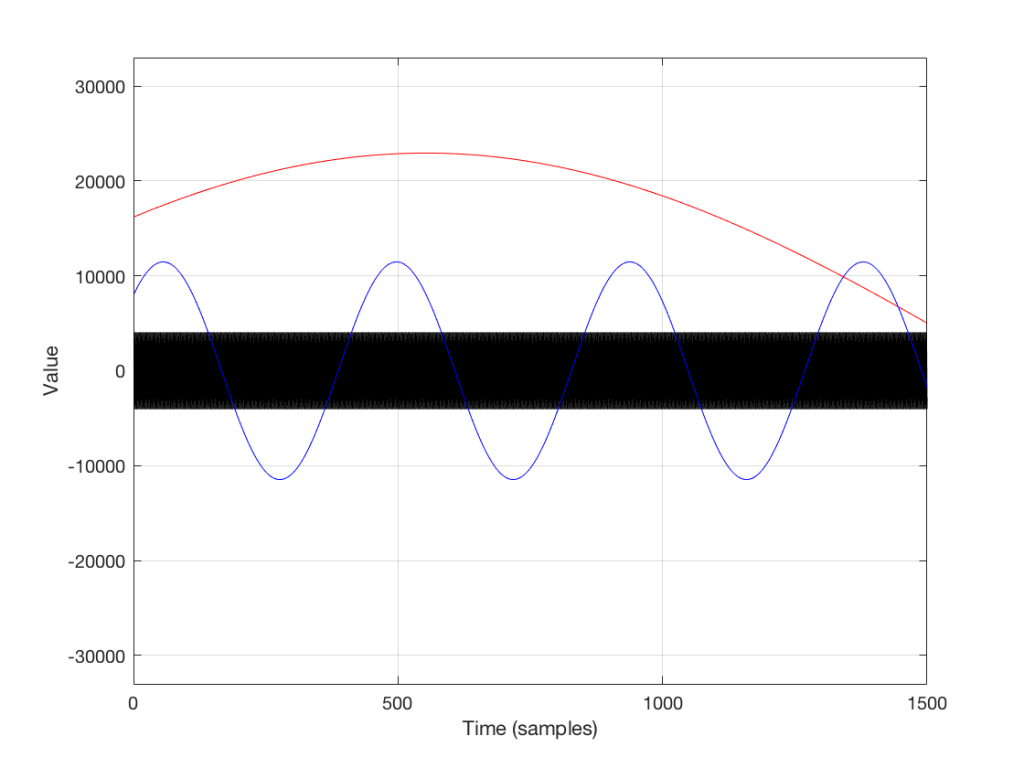
If the frequency of the audio signal is very low, then the two samples (the current one, and the previous one) are very similar in level, as can be seen in the plot in Figures 6 and 7, below. This means, basically, that the output of the filter will be very, very similar to the output, just twice as loud (because it’s the signal plus itself). Another way to think of this is that the current sample of the audio signal and the previous sample of the same signal are essentially “in phase” – and any two audio signals that are “in phase” and added together will give you twice the output.

However, as the frequency of the audio signal gets higher, the relative levels of those two adjacent samples becomes more and more different (because the sampling rate doesn’t change).  One of them will be closer to “0” than the other – and increasingly so as the frequency increases .  So, the higher the audio frequency, the lower the level of the output (since it will not go higher than the signal plus itself, as we saw in the low frequency example…) If we’re thinking of this in terms of phase, the higher the frequency of the audio signal, the greater the phase difference between the adjacent samples that are summed, so the lower the output…

That output level keeps dropping as the audio frequency goes up until we hit a frequency where the audio signal’s frequency is exactly one half of the sampling rate. At that “magic point”, the two samples are so far apart (in terms of the audio signal’s waveform) that they have opposite polarity values (because they’re 180 degrees out-of-phase with each other). So, if you add those two samples together, you get no output – because they are equal, but opposite.

 

 

Let’s zoom in on the plot in Figure 6 to see the individual samples. We’ll take a slice of time around the 500-sample mark. This is shown below in Figure 7.

 

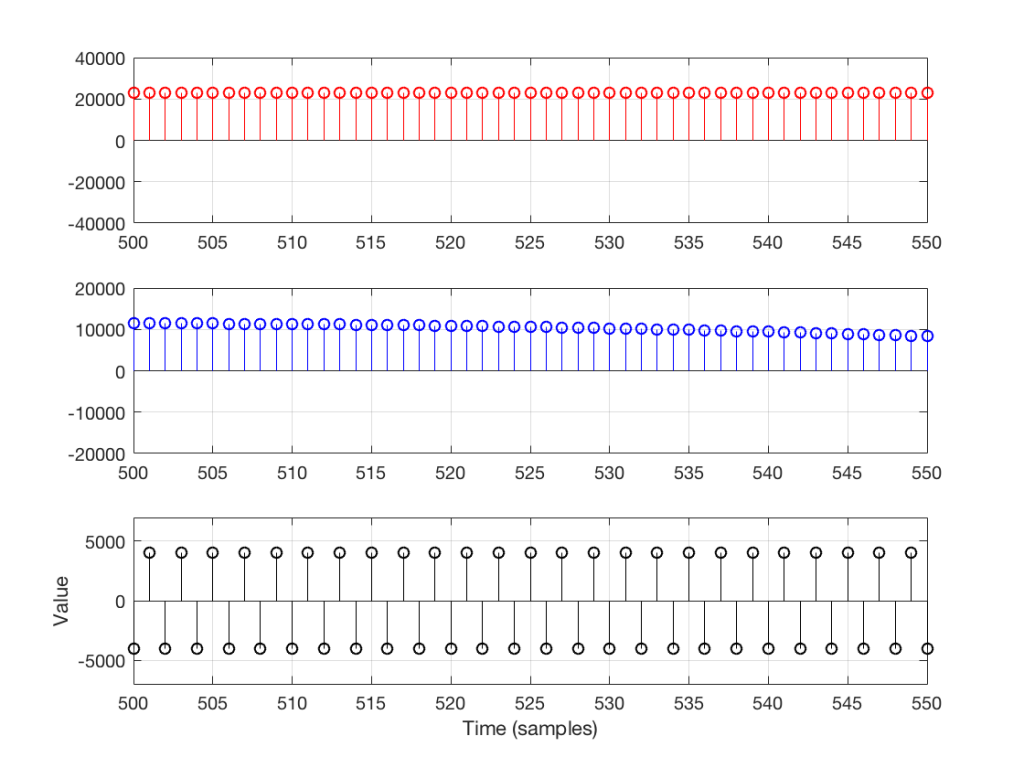
As you can see in Figure 7, any two adjacent samples for a low frequency (the red plot) are almost identical. The middle frequency (the blue plot) shows that two adjacent samples are more different than they are for this low frequency. For the “magic frequency” of “sampling rate divided by 2” (in this case, 22050 Hz) two adjacent samples are equal and opposite in polarity.

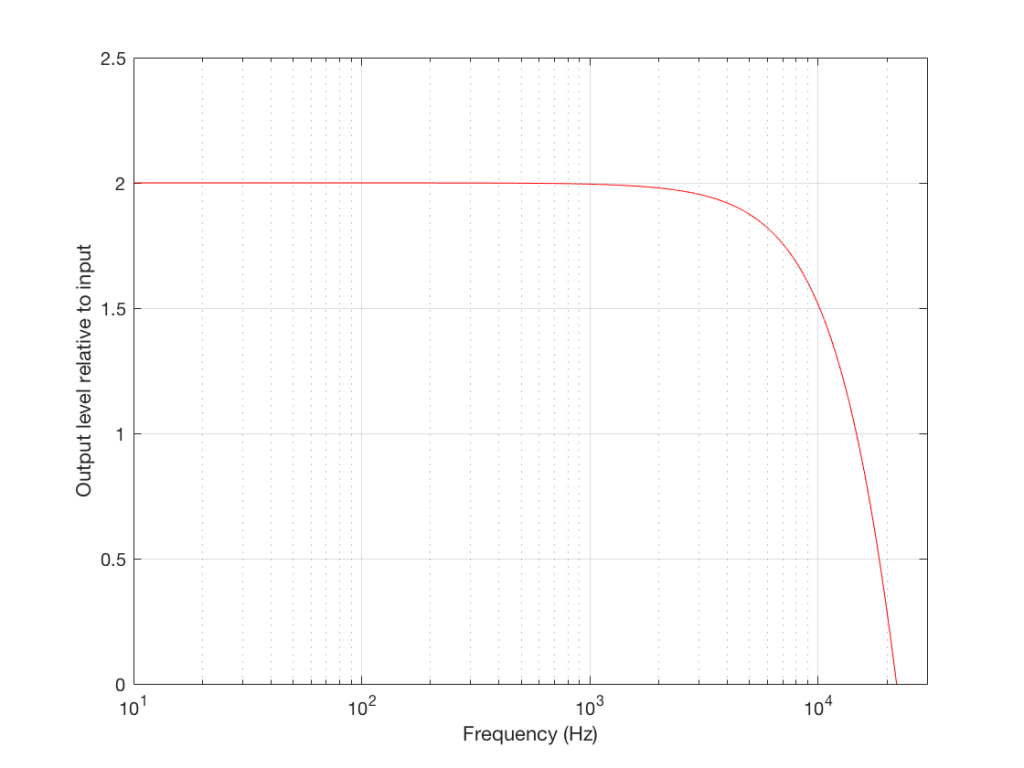
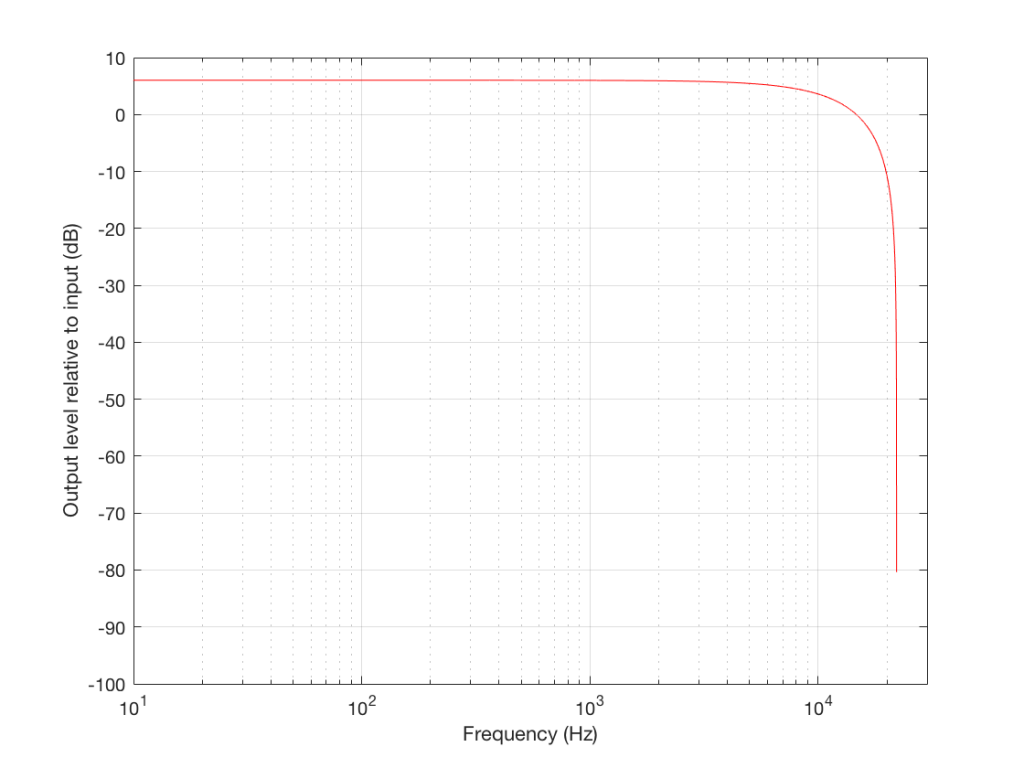
Now that you know this, we are able to “connect the dots” and plot the output levels for the filter in Figure 5 for a range of frequencies from very low to very high. This is shown in Figures 8 and 9, below.

Normalised frequency

Now we have to step up the coefficient of geekiness…

So far, we have been thinking with a fixed sampling rate of 44.1 kHz – just like that which is used for a CD. However, audio recordings that you can buy online are available at different sampling rates – not just 44.1 kHz. So, how does this affect our understanding so far?

Well, things don’t change that much – we just have to change gears a little by making our frequency scales vary with sampling rate.

So, without using actual examples or numbers, we already know that an audio signal with a low frequency going through the filter above will come out louder than the input. We also know that the higher the frequency, the lower the output until we get to the point where the audio signal’s frequency is one half the sampling rate, where we get no output. This is true, regardless of the sampling rate – the only change is that, by changing the sampling rate, we change the actual frequencies that we’re talking about in the audio signal.

So, if the sampling rate is 44.1 kHz, we get no output at 22050 Hz. However, if the sampling rate were 96 kHz, we wouldn’t reach our “no output” frequency until the audio signal gets to 48 kHz (half of 96 kHz). If the sampling rate were 176.4 kHz, we would get something out of our filter up to 88.2 kHz.

So, the filter generally behaves the same – we’re just moving the frequency scale around.

So, instead of plotting the magnitude response of our filter with respect to the actual frequency of the audio signal out here in the real world, we can plot it with respect to the sampling rate, where we can get all the way up to 0.5 (half of the sampling rate) since this is as high as we’re allowed to go. So, I’ve re-plotted Figures 8 and 9 below using what is called a “normalised frequency” scale – where the frequency of the audio signal is expressed as a fraction of the sampling rate.

 

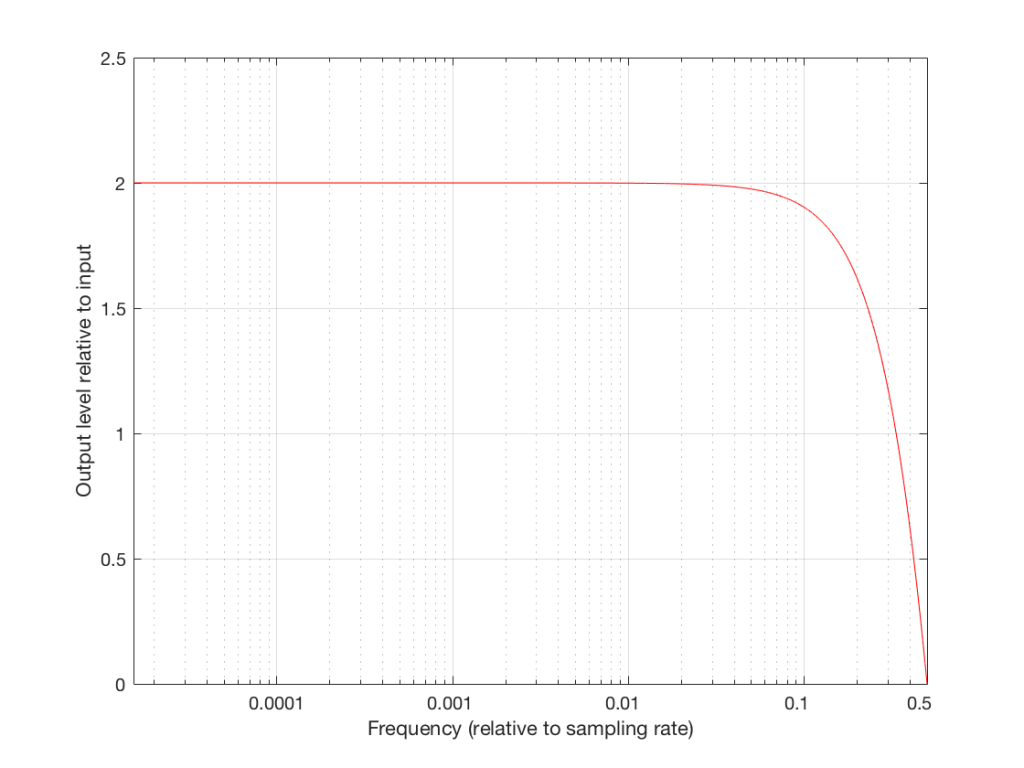
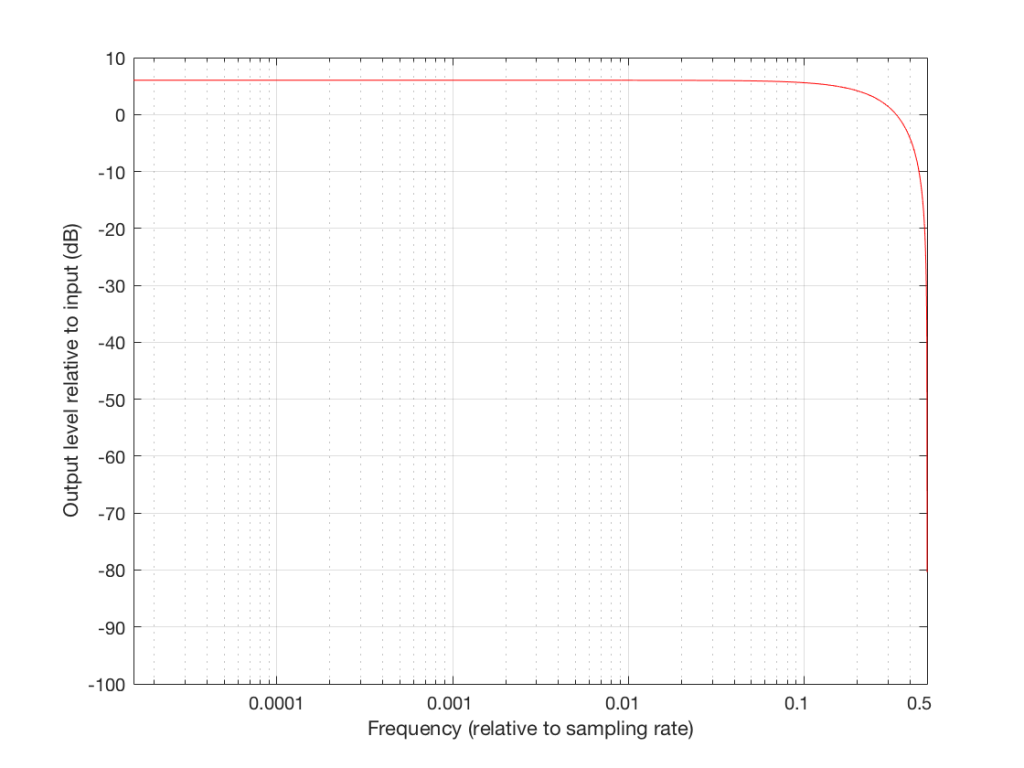
These last sentences are VERY IMPORTANT! So, if you didn’t understand everything I said in the previous 6 paragraphs, go back and read them again. If you still don’t understand it, please email me or put a comment in below, because it means that I didn’t explain it well enough. ..

 

Note that there are two conventions for “normalised frequency” just to confuse everyone. Some people say that it’s “audio frequency relative to the sampling rate” (like I’ve done here). Some other people say that it’s “audio frequency relative to half of the sampling rate”. Now you’ve been warned.

Designing an audio filter

In the example above, I made a basic audio filter, and then we looked at its output. Of course, if we’re making a loudspeaker with digital signal processing, we do the opposite. We have a target response that we want at the output, and we build a filter that delivers that result.

For example, let’s say that I wanted to make a filter that has a similar response to the one shown above, but I want it to roll off less in the high frequencies. How could I do this? One option is shown below in Figure 10:

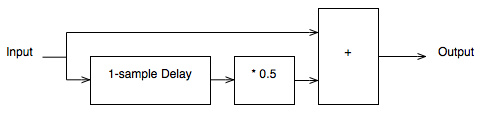
Notice that I added a multiplier on the output of the delay block. This means that if the frequency is low, I’ll add the current sample to half the value of the previous one, so I’ll get a maximum output of 1.5 times the input (instead of 2 like we had before). When we get to one half the sampling rate, we won’t cancel completely, so the high end won’t drop off as much. The resulting magnitude response is shown in Figures 11 and 12, below.

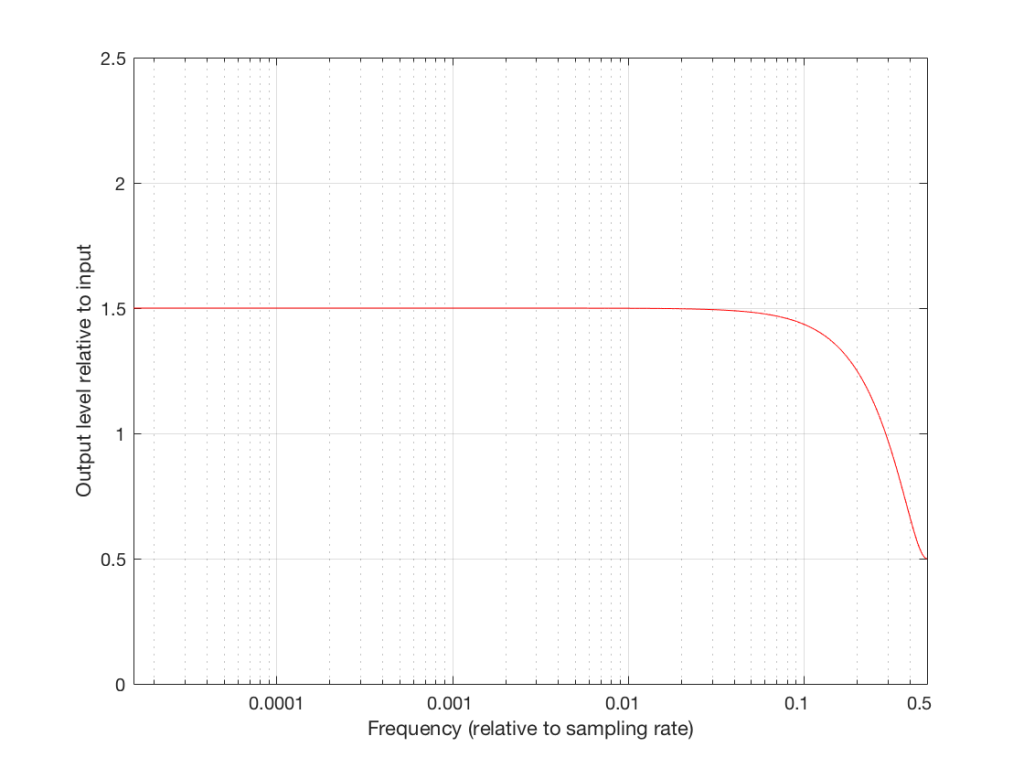
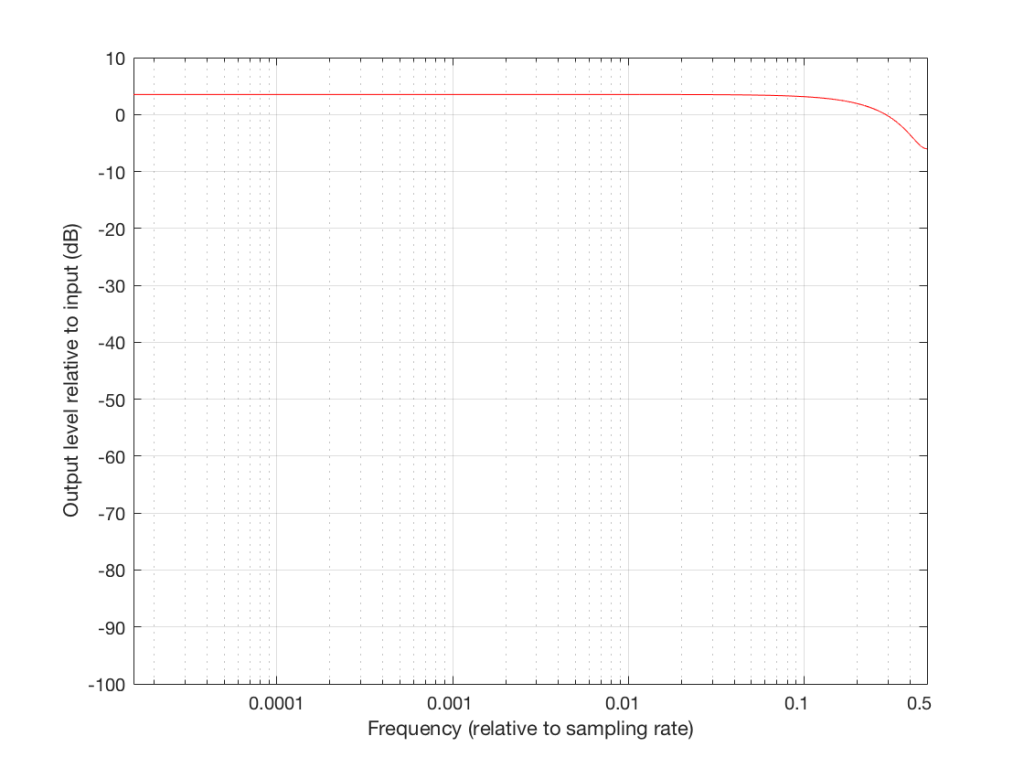
So, we can decide on a response for the filter, and we can design a filter that delivers that response. Part of the design of that filter is the values of the “coefficients” inside it. In the case of digital filters, “coefficient” is a fancy term meaning “number” – in the case of the filter in Figure 10, it has one coefficient – the “0.5” that is multiplied by the output of the delay. For example, if we wanted less of a roll-off in the high end, we could set that coefficient to 0.1, and we would get less cancellation at half the sampling rate (and less output in the low end….)

Putting some pieces together

So, now we see that a digital filter’s magnitude response (and phase response, and other things) is dependent on three things:

• its design (e.g. how many delays and additions)
• the sampling rate
• the coefficients inside it

If we change one of these three things, the magnitude response of the filter will change. This means that, if we want to change one of these things and keep the magnitude response, we’ll have to change at least one of the other things.

For example, if we want to change the sampling rate, but keep the design of the filter, in order to get the same sampling rate, we’re going to have to change the coefficients.

Again, those last two paragraphs were important… Read’em again if you didn’t get it.

So what?

Let’s now take this information into the real world.

In order for BeoLab 90 to work, we had to put a LOT of digital filters into it – and some of those filters contain thousands of coefficients… For example, when you’re changing from “Narrow” mode to “Wide” mode, you have to change a very large filter for each of loudspeaker driver (that’s thousands of coefficients times 18 drivers) – among other things… This has at least four implications:

• there has to be enough computing power inside the BeoLab 90 to make all those multiplications at the sampling rate (which, we’ve already seen above, is very fast)
• there has to be enough computer memory to handle all of the delays that are necessary to build the filters
•  there has to be enough memory to store all of those coefficients (remember that they’re not numbers like 1 or 17 – they’re very precise numbers with a lot of digits like 0.010383285748578423049 (in case you’re wondering, that’s not an actual coefficient from one of the filters in a loudspeaker – I just randomly tapped on a bunch of keys on my keyboard until I got a long number… I’m just trying to make an intuitive point here…))
• You have to be able to move those coefficients from the memory where they’re stored into the calculator (the DSP) quickly because people don’t want to wait for a long time when you’re changing modes

This is why (for now, at least) when you switch between “Narrow” and “Wide” mode, there is a small “break” in the audio signal to give the processor time to load all the coefficients and get the signal going again.

One sneaky thing in the design of the system is that, internally, the processor is always running at the same sampling rate. So, if you have a source that is playing back audio files from your hard drive, one of them ripped from a CD (and therefore at 44.1 kHz) and the next one from www.theflybynighthighresaudiodownloadcompany.com (at 192 kHz), internally at the DSP, the BeoLab 90 will not change.

Why not? Well, if it did, we would have to load a whole new set of coefficients for all of the filters every time your player changes sampling rates, which, in a worst case, is happening for every song, but which you probably don’t even realise is happening – nor should you have to worry about it…

So, instead of storing a complete set of coefficients for each possible sampling rate – and loading a new set into the processor every time you switch to the next track (which, if you’re like my kids, happens after listening to the current song for no more than 5 seconds…) we keep the internal sampling rate constant.

There is a price to pay for this – we have to ensure that the conversion from the sampling rate of the source to the internal sampling rate of the BeoLab 90 is NOT the weakest link in the chain. This is why we chose a particular component (specifically the Texas Instruments SRC4392 – which is a chip that you can buy at your local sampling rate converter store) to do the job. It has very good specifications with respect to passband ripple, signal-to-noise ratio, and distortion to ensure that the conversion is clean. One cost of this choice was that its highest input sampling rate is 216 kHz – which is not as high as the “DXD” standard for audio (which runs at 384 kHz).

So, in the development meetings for BeoLab 90, we decided three things that are linked to each other.

1. we would maintain a fixed internal sampling rate for the DSP, ADC’s and DAC’s.
2. This meant that we would need a very good sampling rate converter for the digital inputs.
3. The choice of component for #2 meant that BeoLab 90’s hardware does not support DXD at its digital inputs.

One of the added benefits to using a good sampling rate converter is that it also helps to attenuate artefacts caused by jitter originating at the audio source – but that discussion is outside the scope of this posting (since I’ve already said far too much…) However, if you’re curious about this, I can recommend a bunch of good reading material that has the added benefit of curing insomnia… Not unlike everything I’ve written here…