As I’ve talked about in a previous posting, when a reciprocal peak/dip filter says “Q”, there’s no knowing what it might mean, because there are at least 7 different definitions of Q (3 for boosts and 4 for dips).

For many people, this doesn’t really matter. If you’re just playing with an EQ to make things sound better right now, then the values on the display really don’t matter: it’s the sound that counts.

If you’re like me, you need to be able to navigate between different pieces of software and hardware, and to get the same EQ response from them, then you’ll also need to know firstly that you can’t trust the display, and secondly, how to “translate” from device to device when necessary.

For example, take a look at Figure 1

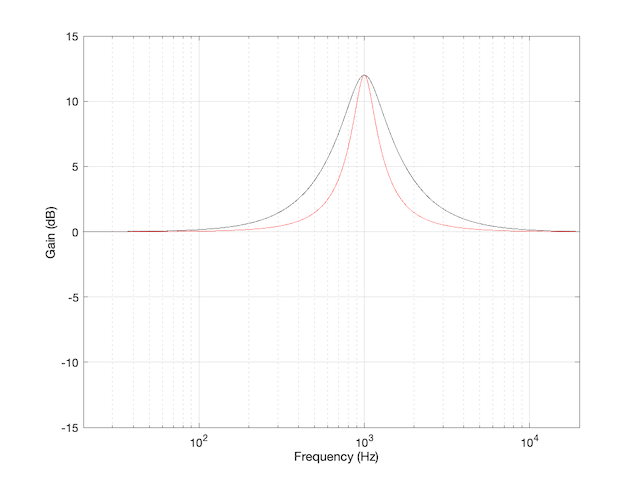
This shows two magnitude responses, however, these are the measurements of two equalisers with identical settings:
Fc = 1 kHz, Gain = +12 dB, Q = 2.

The black curve shows the response of an equaliser that uses the -3 dB points to define the bandwidth of the filter, and therefore the Q is based on 1/(2 zeta). The red curve shows the response of an equaliser that uses the mid-point (in this case, +6 dB because the Gain is +12 dB) to define the bandwidth of the filter.

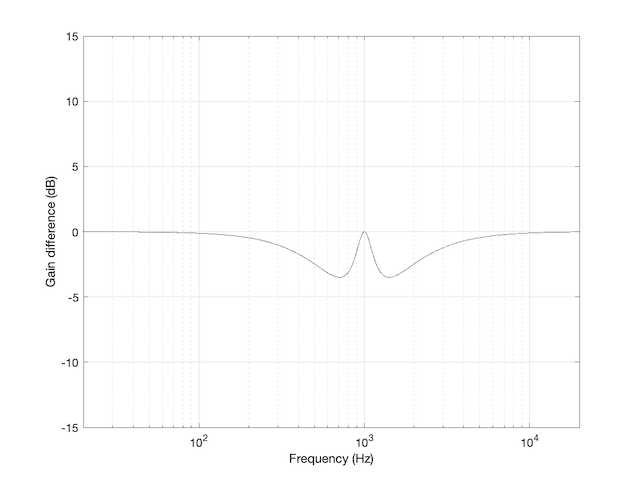
The difference between these two plots is shown below in Figure 2.

We’d have a similar problem if we were cutting instead of boosting, as shown in Figure 3.

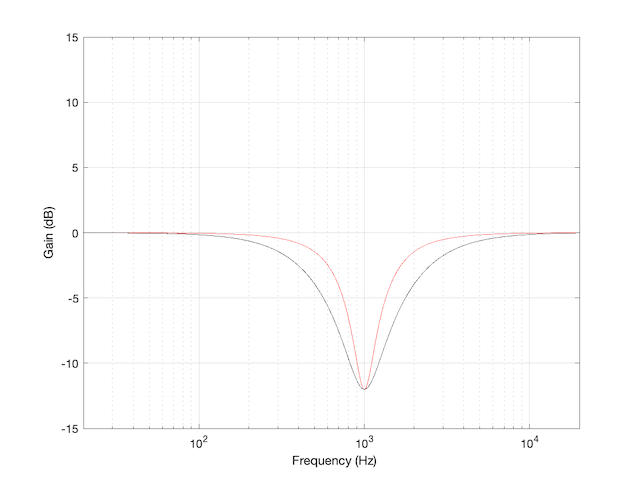
You have to think upside down in this case, because the 1/(2 zeta) filter is actually using the 3 dB UP points to measure bandwidth; but we’ll ignore that and move on.

If you need to translate between the two systems shown above, there’s a pretty easy way to do it.

I’ll assume that you are implementing your filter using the mid-point definition of the bandwidth, so you need to convert into that system rather than out of it. (I’m making this assumption because it’s the one that Robert Bristow-Johnson used in his Audio Cookbook, which was freely copy-and-pasteable, which means that you find it everywhere these days.) Get the parameters from the filter you want to copy.

We’ll call these parameters Fc (for centre frequency, in Hz), (Gain in dB), and . I’m calling it because it’s a Q based on 1/(2 zeta) and we’ll need to keep it separate from our other Q, which I’ll call (for Robert Bristow-Johnson).

Convert the gain into linear.

   

Then do the following:

IF

   

ELSEIF

   

ELSE
your filter isn’t doing anything because

END

Example 1

If you have a -3 dB-based filter with the following parameters:

and you want to implement that using the Bristow-Johnson equations, then you’ll have to use the following parameters:

   

Example 2

If you have a -3 dB-based filter with the following parameters:

and you want to implement that using the Bristow-Johnson equations, then you’ll have to use the following parameters:

   

Two Extra Things…

If the filter that you’re translating FROM is based on Andy Moorer’s design (which is based on the gain mid-point if the gain is within the ±6 dB range, but based on the 3 dB points if it’s outside that), then you’ll have to write your own IF/THEN statements.

If you’re implementing a filter that was specified for RBJ’s equations in a system that’s based on 1/(2 zeta), then you’re probably smart enough to figure out how to do the above in reverse.

One additional addendum

IF
you don’t like IF/THEN statements for some reason or another (code optimisation, for example)

THEN
you could do it this way instead:

   

What I’ve done there is to fold the decibel-to-linear conversion into the equation. I’ve also converted the gain in dB to an absolute value before converting to linear. That way, it’s always positive, so you always divide.