This will be a short one.

In Part 7, I showed the power responses of three loudspeakers made with point-source (and therefore perfectly omnidirectional at all frequencies, which also means that they have the same response in all direction) drivers.

In that posting, I calculated the power response for a loudspeaker made of two loudspeaker drivers, floating in space, with the assumption that both drivers are point-sources, and that they do not live in an enclosure that has any acoustical effects. I also calculated the responses for 3 different distances between the drivers, which were chosen as a function of the crossover frequency’s wavelength.

One of the crossover types whose power responses that I showed was the 4th-order Linkwitz Riley. The plots that I showed back then for that crossover type is reproduced here in Figure 14.1.

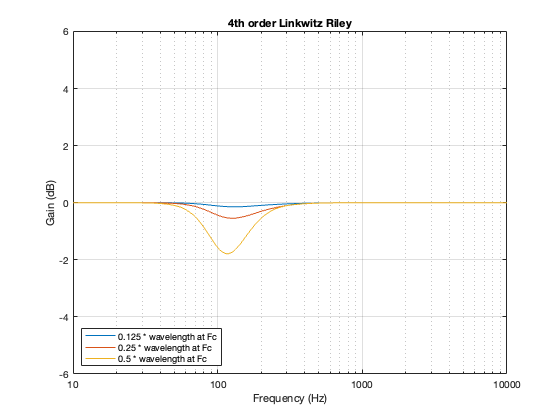
As I said, the details of how I calculated these power responses is detailed in Part 7.

I calculated the power responses for a similar loudspeaker, using a linear phase crossover (with a really long window to avoid any discussion about this…) and with the same crossover frequency of 100 Hz and the same distances between the “drivers”. These power responses are shown below in Figure 14.2.

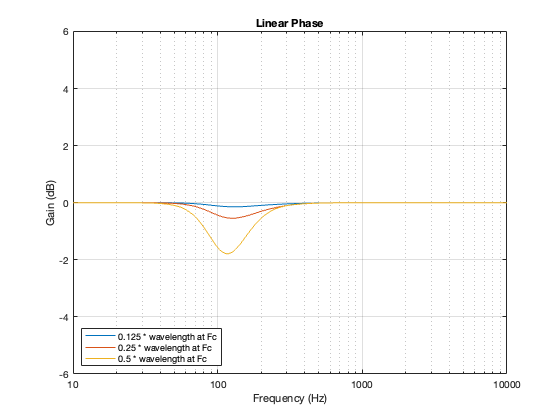
If you look at Figures 14.1 and 14.2 you could be forgiven for thinking that they look VERY similar. In fact, they’re essentially identical. This is because the 0º difference in phase caused by the linear phase crossover is the same as a 360º difference in phase caused by the 4th order Linkwitz Riley.

In other words, the message of this posting is that the power responses of a loudspeaker that has been implemented with a 4th order Linkwitz Riley crossover and the same loudspeaker with a linear phase crossover will have the same power responses, assuming that all other aspects of the loudspeaker are the same.