This will be a short posting with very little new information. I’m just starting to put some of the Lego blocks together to make it easier later on.
For this posting, I’ve taken two different pieces of information that you already have, and put them together.
2nd order Butterworth
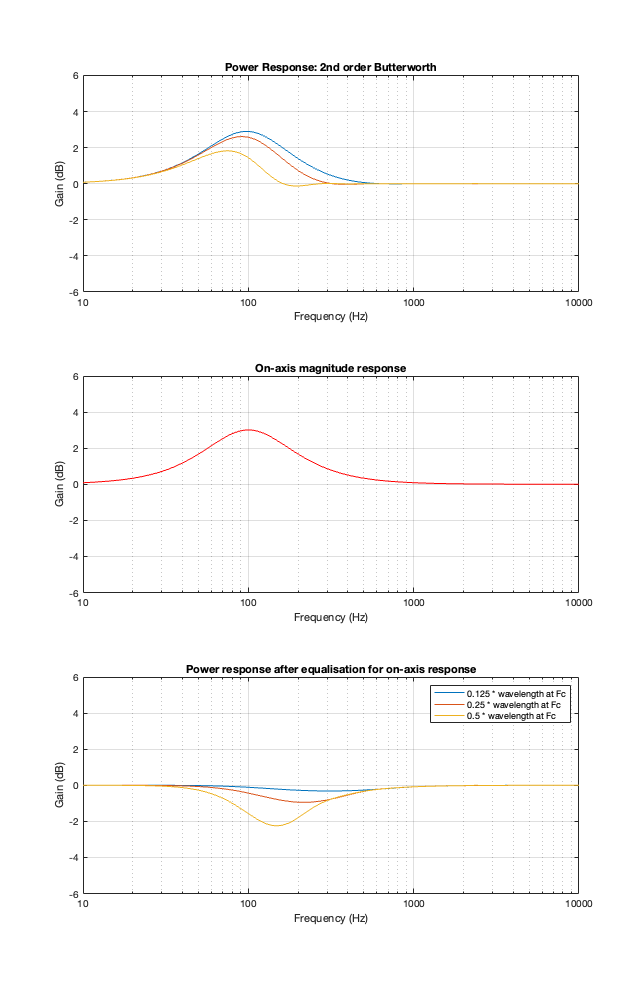
Take a look at Figure 8.1 below, which shows information related to a 2nd order Butterworth crossover at 100 Hz.
The top plot shows the power responses, explained in Part 7.
The middle plot shows the on-axis magnitude response, which will be the same regardless of the separation between the loudspeaker drivers because I’m assuming that they’re perfect point-sources.
IF you built such a loudspeaker, then chances are that you would put in an equaliser at the input of your loudspeaker to make the on-axis response flat instead of having that bump. That equaliser would, in turn effect the entire power response. So, the bottom plots show the power responses of the loudspeaker (with three different driver separations) AFTER you’ve applied the equalisation to correct for the on-axis magnitude response.
In other words, the top plots MINUS the middle red plot equals the bottom plots
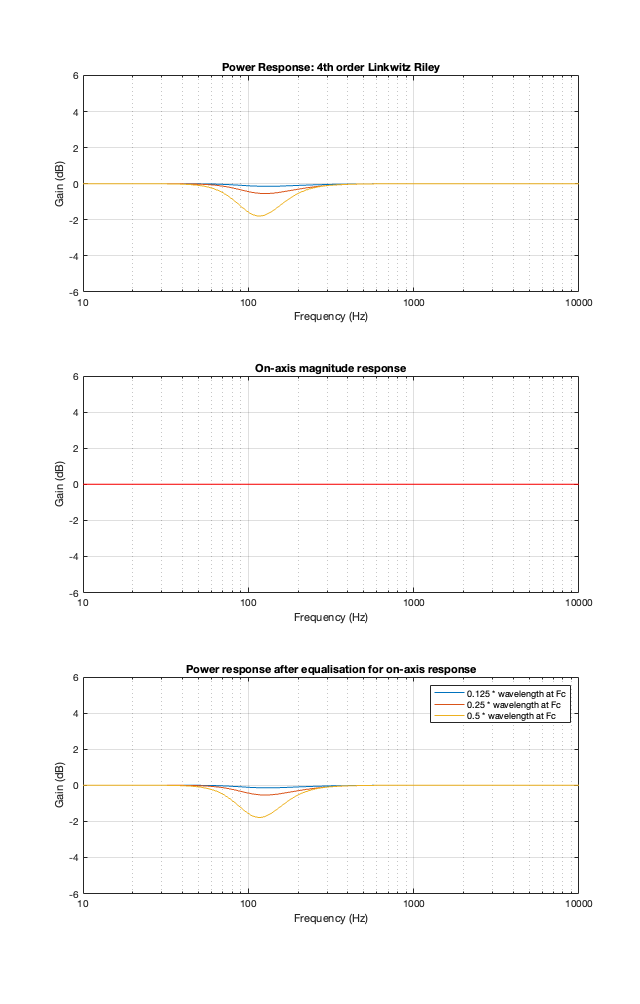
4th-order Linkwitz Riley
The 4th-order Linkwitz Riley’s power response does not change because its on-axis response is flat, so there’s nothing to correct.
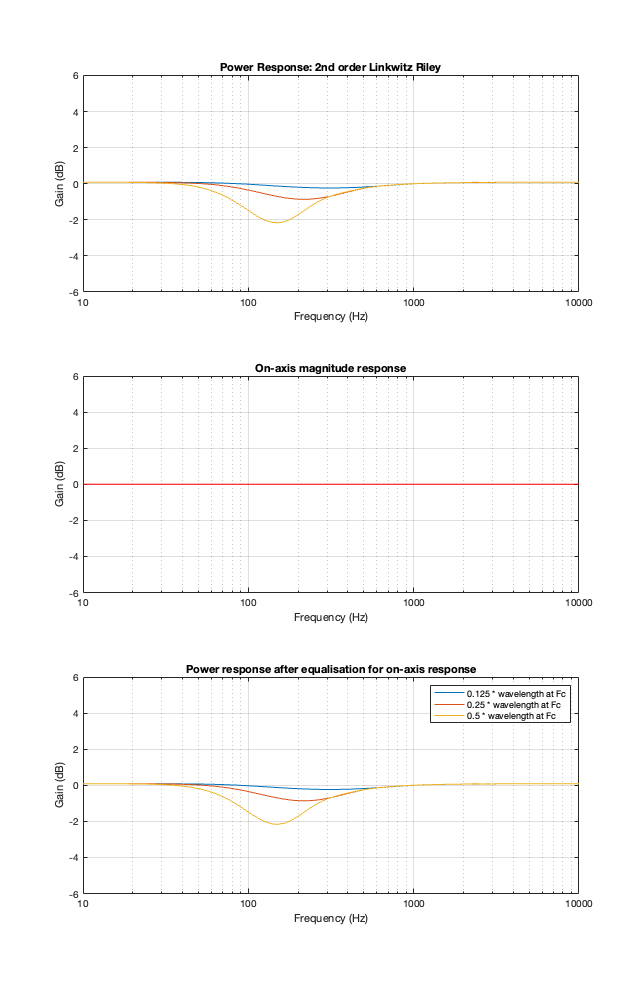
2nd-order Linkwitz Riley
The 2nd-order Linkwitz Riley’s power response does not change because its on-axis response is flat, so there’s nothing to correct.
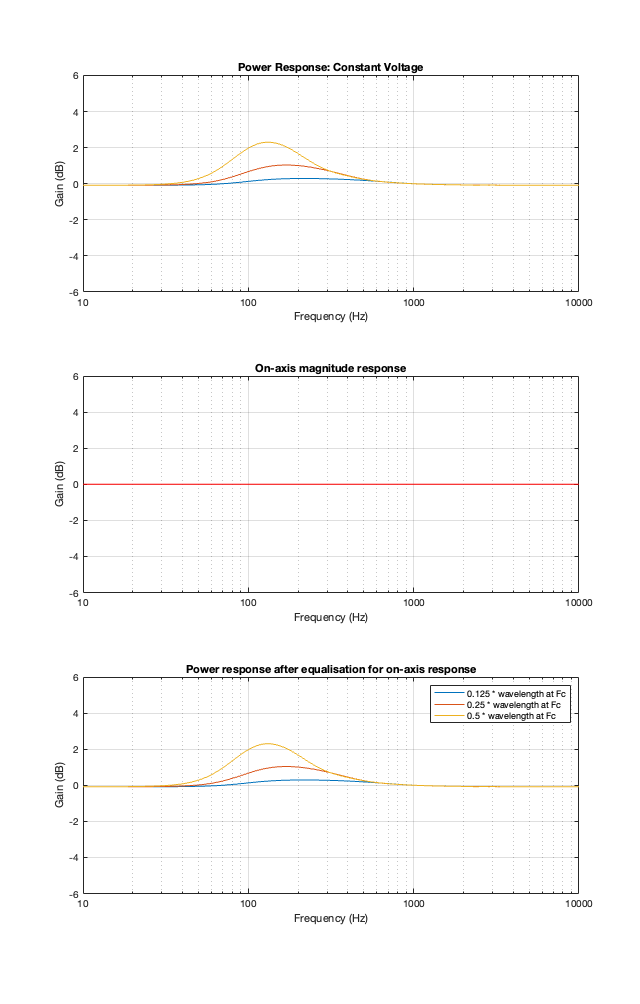
Constant Velocity
The Constant Velocity’s power response does not change because its on-axis response is flat, so there’s nothing to correct.
Like I said: there’s no new information here. It’s just a reminder that, if you add equalisation for your on-axis response (whether this is part of your loudspeaker-building process or your installation in the listening room), you will also have a subsequent on the power response. Since the equalisation is applied to the loudspeaker’s input, the on-axis and power responses are locked together. Change one, and you change them both.