
Thanks to George Massenburg at GML Inc. (www.massenburg.com) for his kind permission to use include this chapter which was originally written as part of a manual for one of their products.
Once upon a time, in the days before audio was digital, when you made a long-distance phone call, there was an actual physical connection made between the wire running out of your phone and the phone at the other end. This caused a big problem in signal quality because a lot of high-frequency components of the signal would get attenuated along the way. Consequently, booster circuits were made to help make the relative levels of the various frequencies equal. As a result, these circuits became known as equalizers. Nowadays, of course, we don’t need to use equalizers to fix the quality of long-distance phone calls, but we do use them to customize the relative balance of various frequencies in an audio signal.
In order to look at equalizers and their smaller cousins, filters, we’re going to have to look at their frequency response curves. This is a description of how the output level of the circuit compares to the input for various frequencies. We assume that the input level is our reference, sitting at 0 dB and the output is compared to this, so if the signal is louder at the output, we get values greater than 0 dB. If it’s quieter at the output, then we get negative values at the output.
Before diving straight in and talking about how equalizers behave, we’ll start with the basics and look at four different types of filters. Just like a coffee filter keeps coffee grinds trapped while allowing coffee to flow through, an audio filter lets some frequencies pass through unaffected while reducing the level of others.
One of the conceptually simplest filters is known as a low-pass filter because it allows low frequencies to pass through it. The question, of course, is “how low is low?” The answer lies in a single frequency known as the cutoff frequency or fc. This is the frequency where the output of the filter is 3.01 dB lower than the maximum output for any frequency (although we normally round this off to -3 dB which is why it’s usually called the 3 dB down point). “What’s so special about -3 dB?” I hear you cry. This particular number is chosen because -3 dB is the level where the signal is at one half the power of a signal at 0 dB. So, if the filter has no additional gain incorporated into it, then the cutoff frequency is the one where the output is exactly one half the power of the input. (Which explains why some people call it the half-power point.)
As frequencies get higher and higher, they are attenuated more and more. This results in a slope in the frequency response graph which can be calculated by knowing the amount of extra attenuation for a given change in frequency. Typically, this slope is specified in decibels per octave. Since the higher we go, the more we attenuate in a low pass filter, this value will always be negative.

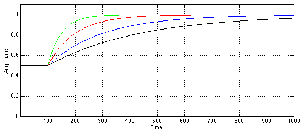
The slope of the filter is determined by its order. If we oversimplify just a little, a first-order low-pass filter will have a slope of -6.02 dB per octave above its cutoff frequency (usually rounded to -6 dB/oct). If we want to be technically correct about this, then we have to be a little more specific about where we finally reach this slope. Take a look at the frequency response plot in Figure 6.1. Notice that the graph has a nice gradual transition from a slope of 0 (a horizontal line) in the really low frequencies to a slope of -6 dB/oct in the really high frequencies. In the area around the cutoff frequency, however, the slope is changing. If we want to be really accurate, then we have to say that the slope of the frequency response is really 0 for frequencies less than one tenth of the cutoff frequency. In other words, for frequencies more than one decade below the cutoff frequency. Similarly, the slope of the frequency response is really -6.02 dB/oct for frequencies more than one decade above (ten times) the cutoff frequency.
If we have a higher-order filter, the cutoff frequency is still the one where the output drops by 3 dB, however the slope changes to a value of -6.02n dB/oct, where n is the order of the filter. For example, if you have a 3rd-order filter, then the slope is
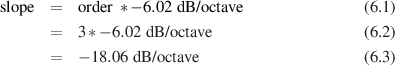
A high-pass filter is essentially exactly the same as a low-pass filter, however, it permits high frequencies to pass through while attenuating low frequencies as can be seen in Figure 6.2. Just like in the previous section, the cutoff frequency is where the output has a level of -3.01 dB but now the slope below the cutoff frequency is positive because we get louder as we increase in frequency. Just like the low-pass filter, the slope of the high-pass filter is dependent on the order of the filter and can be calculated using the equation 6.02n dB/oct, where n is the order of the filter.
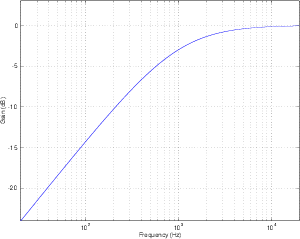
Remember as well that the slope only applies to frequencies that are at least one decade away from the cutoff frequency.
Let’s take a signal and send it through a high-pass filter and a low-pass filter in series, so the output of one feeds into the input of the other. Let’s also assume for a moment that the two cutoff frequencies are more than a decade apart.
The result of this probably won’t hold any surprises. The high-pass filter will attenuate the low frequencies, allowing the higher frequencies to pass through. The low-pass filter will attenuate the high frequencies, allowing the lower frequencies to pass through. The result is that the high and low frequencies are attenuated, with a middle band (called the passband) that’s allowed to pass relatively unaffected.
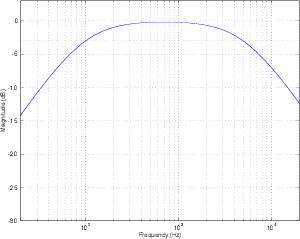
The system described in the previous section is called a bandpass filter and it has a couple of specifications that we should have a look at. The first is the width of the passband. This bandwidth is calculated using the difference two cutoff frequencies which we’ll label fc1 for the lower one and fc2 for the higher one. Consequently, the bandwidth is calculated using the equation:
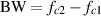 | (6.4) |
So, using the example of the filter frequency response shown in Figure 6.3, the bandwidth is 5,000 Hz – 100 Hz = 4900 Hz.
We can also calculate the middle of the passband using these two frequencies. It’s not quite so simple as we’d like, however. Unfortunately, it’s not just the frequency that’s half-way between the low and high frequency cutoff’s. This is because frequency specifications don’t really correspond to the way we hear things. Humans don’t usually talk about frequency – they talk about pitches and notes. They say things like “Middle C” instead of “262 Hz.” They also say things like “one octave” or “one semitone” instead of things like “a bandwidth of 262 Hz.”
Consider that, if we play the A below Middle C on a well-tuned piano, we’ll hear a note with a fundamental of 220 Hz. The octave above that is 440 Hz and the octave above that is 880 Hz. This means that the bandwidth of the first of these two octaves is 220 Hz (it’s 440 Hz – 220 Hz), but the bandwidth of the second octave is 440 Hz (880 Hz – 440 Hz). Despite the fact that they have different bandwidths, we hear them each as one octave, and we hear the 440 Hz note as being half-way between the other two notes. So, how do we calculate this? We have to find what’s known as the geometric mean of the two frequencies. This can be found using the equation

Let’s say that you want to build a bandpass filter with a bandwidth of one octave. This isn’t difficult if you know the centre frequency and if it’s never going to change. For example, if the centre frequency was 440 Hz, and the bandwidth was one octave wide, then the cutoff frequencies would be 311 Hz and 622 Hz (we won’t worry too much at the moment about how I arrived at these particular numbers). What happens if we leave the bandwidth the same at 311 Hz, but change the centre frequency to 880 Hz? The result is that the bandwidth is now no longer an octave wide – it’s one half of an octave. So, we have to link the bandwidth with the centre frequency so that we can describe it in terms of a fixed musical interval (for you engineers, a musical interval is a measure of the distance between two notes). This is done using what is known as the quality or Q of the filter, calculated using the equation:

Now, instead of talking about the bandwidth of the filter, we can use the Q which gives us an idea of the width of the filter in musical terms. This is because, as we increase the centre frequency, we have to increase the bandwidth proportionately to maintain the same Q. Notice however, that if we maintain a centre frequency, the smaller the bandwidth gets, the bigger the Q becomes, so if you’re used to talking in terms of musical intervals, you have to think backwards. The bigger the Q, the smaller the interval.
Remember that you can have a very high Q, and therefore a very narrow bandwidth for a bandpass filter. All of the definitions still hold, however. The cutoff frequencies are still the points where we’re 3 dB lower than the maximum value and the bandwidth is still the distance in Hertz between these two points and so on...
Although bandpass filters are very useful at accentuating a small band of frequencies while attenuating others, sometimes we want to do the opposite. What if we want to attenuate a small band of frequencies while leaving the rest alone? This can be accomplished using a band-reject filter (also known as a bandstop filter) which, as its name implies, rejects (or usually just attenuates) a band of frequencies without affecting the surrounding material. The frequency response of this can be seen in Figure 6.4.
The thing to be careful of when describing band-reject filters is the fact that cutoff frequencies are still defined as the points where we’ve dropped in level by 3 dB from the maximum output.
There is a special breed of band-reject filter that is designed to have almost infinite attenuation at a single frequency, leaving all others intact. This, of course is impossible, but we can come close. If we have a band-reject filter with a very high Q, the result is a frequency response like the one shown in Figure 6.5. The shape is basically a flat frequency response with a narrow, deep notch at one frequency – hence the name notch filter
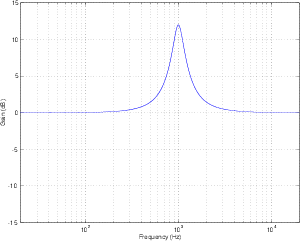
There is a variation on the bandpass filter that, instead of attenuating all frequencies outside the passband, the filter typically leaves them at a gain of 0 dB. This kind of filter can be seen in the plot of an in Figure 6.6 and is called a peaking filter or peak filter. Notice now that, rather than attenuating all unwanted frequencies, the filter can be thought of as simply applying a known gain in the passband. The further away you get from the passband, the less the signal is affected. Notice, however, that we still measure the bandwidth using the two points that are 3 dB down from the peak of the curve.
In most instances of these kinds of filters, it is also possible to attenuate the same frequency band, as is shown in Figure 6.10. Since the practical implementation of this filter allows you to boost and attenuate, they are commonly known of as peak/dip filters.
Unlike its counterpart from the days of long-distance phone calls, a modern equalizer is a device that is capable of attenuating and boosting frequencies according to the desire and expertise of the user. There are four basic types of equalizers, but we’ll have to talk about a couple of issues before getting into the nitty-gritty.
An equalizer typically consists of a collection of filters, each of which permits you to control one or more of three things: the gain, centre frequency and Q of the filter. There are some minor differences in these filters from the ones we discussed above, but we’ll sort that out before moving on. Also, the filters in the equalizer may be connected in parallel or in series, depending on the type of equalizer and the manufacturer.
To begin with, as we’ll see, a filter in an equalizer comes in two basic models, the peak/dip filter and the shelving filter which is a type of variation on the highpass and low pass filters.
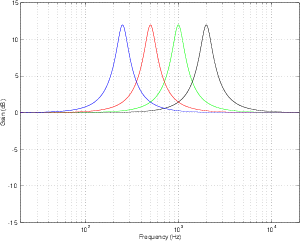
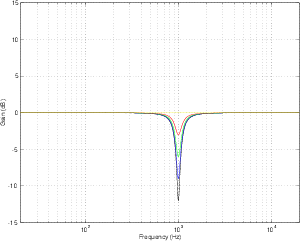
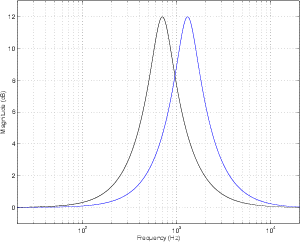
Let’s look at the frequency response of a filter with a centre frequency of 1 kHz, a Q of 4 and a two different amounts of boost or cut. If we plot these responses on the same graph, they look like Figure 6.11.
Notice that, although these two curves have “matching” parameters, they do not have the same shape. This is because the bandwidth (and therefore the Q) of a filter is measured using its 3 dB down point – not the point that’s 3 dB away from the peak or dip in the curve. Since the measurement is not symmetrical, the curves are not symmetrical. This is true of any filter where the Q is kept constant and gain is modified. If you compare a boost of any amount with a cut of the same amount, you’ll always get two different curves. This is what is known as a constant Q filter because the Q is kept as a constant. The result is called an asymmetrical filter (or non-symmetrical filter) because a matching boost and cut are not mirror images of each other.
There are advantages and disadvantages to this type of filter. The primary advantage is that you can have a very selective cut if you’re trying to eliminate a single frequency, simply by increasing the Q. The primary disadvantage is that you cannot undo what you have done. This last statement is explained in the following section.
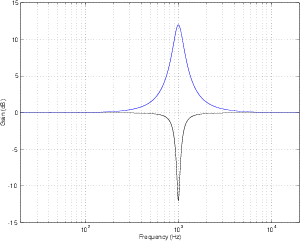
Instead of building a filter where the cut and boost always maintain a constant Q, let’s set about to build a filter that is symmetrical – that is to say that a matching boost and cut at the same centre frequency would result in the same shape. The nice thing about this design is that, if you take two such filters and connect them in series and set their parameters to be the same but opposite gains (for example, both with a centre frequency of 1 kHz and a Q of 2, but one has a boost of 6 dB and the other has a cut of 6 dB) then they’ll cancel each other out and your output will be identical to your input. This also applies if you’ve equalized something while recording – assuming that you live in a perfect world, if you remember your original settings on the recorded EQ curve, you can undo what you’ve done by duplicating the settings and inverting the gain. As a result, we call this a reciprocal peak/dip filterfilter, reciprocal peak/dip.
Let’s take two reciprocal peak/dip filters, each set with a Q of 2 and a gain of 6 dB. The only difference between them is that one has a centre frequency of 700 Hz and the other has a centre frequency of 1.3 kHz. If we use both of these filters on the same signal simultaneously, we can achieve two very different resulting frequency responses, depending on how they’re connected.
If the two filters are connected in series (it doesn’t matter what order we connect them in), then the frequency band that overlaps in the boosted portion of the two filters’ responses will be boosted twice. In other words, the signal goes through the first filter and is amplified, after which it goes through the second filter and the amplified signal is boosted further. This arrangement is also known as a circuit made of combining filters.
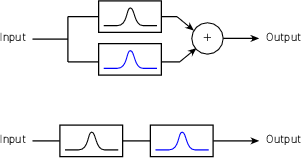
If we connect the two filters in parallel, however, a different situation occurs. Now each filter boosts the original signal independently, and the two resulting signals are added, producing a small increase in level, but not as significant as in the case of the series connection. This arrangement is also known as a circuit made of non-combining filters.
The primary advantage to having filters in connected in series rather than in parallel lies in possibility of increased gain or attenuation. For example, if you have two filters in series, each with a boost of 12 dB and with matched centre frequencies, the total resulting gain applied to the signal is 24 dB (because a gain of 12 dB from the second filter is applied to a signal that already has a gain of 12 dB from the first filter). If the same two filters were connected in parallel, the total maximum gain would be only 18 dB. (This is because a the addition of two identical signals results in a doubling of level which corresponds to an additional gain of only 6 dB. Note as well that the overall gain of a parallel connection is 6 dB.)
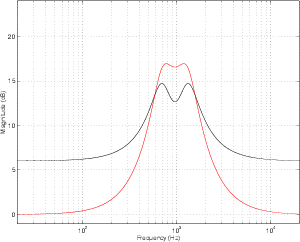
The main disadvantage to having filters connected in series rather than in parallel is the fact that you can occasionally result in frequency bands being boosted more than you’re intuitively aware. For example, looking at Figure 6.16, we can see that, based on the centre frequencies of the two filters, we would expect to have two narrow peaks in the total frequency response at 700 Hz and 1.3 kHz. The actual result, as can be seen, is a (sort of...) single broad peak between the two expected centre frequencies. Also, it should be noted that a group of non-combining filters will likely a ripple in their output frequency response.
The nice thing about high pass and low pass filters is that you can reduce (or eliminate) things you don’t want (like low-frequency noise from air conditioners, for example.) But, what if you want to boost all your low frequencies instead of cutting all your high’s? This is when a shelving filter comes in handy. The response curve of shelving filters most closely resemble their high- and low-pass filter counterparts with a minor difference. As their name suggests, the curve of these filters level out at a specified frequency called the stop frequency. In addition, there is a second defining frequency called the turnover frequency which is the frequency at which the response is 3 dB above or below 0 dB. This is illustrated in Figure 6.17.
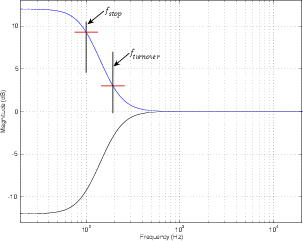
The transition ratio is sort of analogous to the order of the filter and is calculated using the turnover and stop frequencies as shown below.

where RT is the transition ratio.
The closer the transition ratio is to 1, the greater the slope of the transition in gain from the unaffected to the affected frequency ranges. This is because if RT = 1 then fstop = fturnover.
These filters are available as high- and low-frequency shelving units, boosting high and low frequencies respectively. In addition, they typically have a symmetrical response. If the transition ratio is less than 1, then the filter is a low shelving filter. If the transition ratio is greater than 1, then the filter is a high shelving filter.
The disadvantage of these components lies in their potential to boost frequencies above and below the audible audio range causing at the least wasted amplifier power and at the worst, loudspeaker damage. For example, if you use a high shelf filter with a stop frequency of 10 kHz to increase the level of the high end by 12 dB to brighten things up a bit, you will probably also wind up boosting signals above your hearing range. In a typical case, this may cause some unpredictable signals from your tweeter due to increased intermodulation distortion of signals you can’t even hear. To reduce these unwanted effects, super sonic and subsonic signals can be attenuated using a low pass or high pass filter respectively outside the audio band. Using a peaking filter at the appropriate frequency instead of a filter with a shelving response can avoid the problem altogether.
The most common application of this equalizer is the tone controls on home sound systems. These bass and treble controls generally have a maximum slope of 6 dB per octave and reciprocal characteristics. They are also frequently seen on equalizer modules on small mixing consoles.
Graphic equalizers are seen just about everywhere these days, primarily because they’re intuitive to use. In fact, they are probably the most-used piece of signal processing equipment in recording. The name “graphic equalizer” comes from the fact that the device is made up of a number of filters with centre frequencies that are regularly spaced, each with a slider used for gain control. The result is that the arrangement of the sliders gives a graphic representation of the frequency response of the equalizer. The most common frequency resolutions available are one-octave, two-third-octave and one-third-octave, although resolutions as fine as one-twelveth-octave exist. The sliders on most graphic equalizers use ISO standardized band center frequencies (See Section 12.1). They almost always employ reciprocal peak/dip filters wired in parallel. As a result, when two adjacent bands are boosted, there remains a comparatively large dip between the two peaks. This proves to be a great disadvantage when attempting to boost a frequency between two center frequencies. Drastically excessive amounts of boost may be required at the band centers in order to properly adjust the desired frequency. This problem is eliminated in graphic EQ’s using the much-less-common combining filters. In this system, the filter banks are wired in series, thus adjacent bands have a cumulative effect. Consequently, in order to boost a frequency between two center frequencies, the given filters need only be boosted a minimal amount to result in a higher-boosted mid-frequency.
Virtually all graphic equalizers have fixed frequencies and a fixed Q. This makes them simple to use and quick to adjust, however they are generally a compromise. Although quite suitable for general purposes, in situations where a specific frequency or bandwidth adjustment is required, they will prove to be inaccurate.
One attempt to overcome the limitations of the graphic equalizer is the paragraphic equalizer. This is a graphic equalizer with fine frequency adjustment on each slider. This gives the user the ability to sweep the center frequency of each filter somewhat, thus giving greater control over the frequency response of the system.
These equalizers are most commonly found on the input stages of mixing consoles. They are generally used where more control is required over the signal than is available with graphic equalizers, yet space limitations restrict the sheer number of potentiometers available. Typically, the equalizer section on a console input strip will have one or two sweep filters in addition to low and a high shelf filters with fixed turnover frequencies. The frequencies of the mid-range filters are usually reciprocal peak/dip filters with an adjustable (or sweepable) center frequencies and fixed Q’s.
The advantage of this configuration is a relatively versatile equalizer with a minimum of knobs, precisely what is needed on an overcrowded mixer panel. The obvious disadvantage is its lack of adjustment on the bandwidth, a problem that is solved with a parametric equalizer.
A parametric equalizer is one that allow the user to control the gain, centre frequency and Q of each filter. In addition, these three parameters are independent – that is to say that adjusting one of the parameters will have no effect on the other two. They are typically comprised of combining filters and will have either reciprocal peak/dip or constant-Q filters. (Check your manual to see which you have – it makes a huge difference!) In order to give the user a wider amount of control over the signal, the frequency ranges of the filters in a parametric equalizer typically overlap, making it possible to apply gain or attenuation to the same centre frequency using at least two filters.
The obvious advantage of using a parametric equalizer lies in the detail and versatility of control afforded by the user. This comes at a price, however – it unfortunately takes much time and practice to master the use of a parametric equalizer.
A less expensive variation on the true parametric equalizer is the semi-parametric equalizer or quasi-parametric equalizer. From the front panel, this device appears to be identical to its bigger cousin, however, there is a significant difference between the two. Whereas in a true parametric equalizer, the three parameters are independent, in a semi-parametric equalizer, they are not. As a result, changing the value of one parameter will cause at least one, if not both, of the other two parameters to change unexpectedly. As a result, although these devices are less expensive than a true parametric, they are less trustworthy and therefore less functional in real working situations.
| Category | Graphic | Parametric
| |||
| Control | Graphic | Paragraphic | Sweep | Semi-parametric | True Parametric |
| Gain | Y | Y | Y | Y | Y |
| Centre Frequency | N | Y | Y | Y | Y |
| Q | N | N | N | Y | Y |
| Shelving Filter? | N | N | Y | Optional | Optional |
| Combining / Non-combining | N | N | N | Depends | C |
| Reciprocal peak/dip or Constant Q | R p/d | R p/d | R p/d | Typically R p/d | Depends |
So far, we’ve only been looking at the frequency response of a filter or equalizer. In other words, we’ve been looking at what the magnitude of the output of the filter would be if we send sine tones through it. If the filter has a gain of 6 dB at a certain frequency, then if we feed it a sine tone at that frequency, then the amplitude of the output will be 2 times the amplitude of the input (because a gain of 2 is the same as an increase of 6 dB). What we haven’t looked at so far is any shift in phase (also known as phase distortion) that might be incurred by the filtering process. Any time there is a change in the frequency response in the signal, then there is an associated change in phase response that you may or may not want to worry about. That phase response is typically expressed as a shift (in degrees) for a given frequency. Positive phase shifts mean that the signal is delayed in phase whereas negative phase shifts indicate that the output is ahead of the input.
“The output is ahead of the input!?” I hear you cry. “How can the output be ahead of the input? Unless you’ve got one of those new digital filters that can see into the near future...” Well, it’s actually not as strange as it sounds. The thing to remember here is that we’re talking about a sine wave – so don’t think about using an equalizer to help your drummer get ahead of the beat... It doesn’t mean that the whole signal comes out earlier than it went in. This is because we’re not talking about negative delay – it’s negative phase.
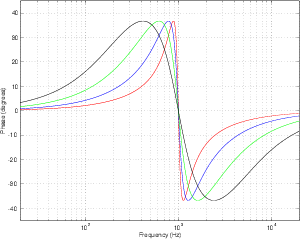
While it’s true that a change in frequency response of a signal necessarily implies that there is a change in its phase, you don’t have to have the same phase shift for the same frequency response change. In fact, different manufacturers can build two filters with centre frequencies of 1 kHz, gains of 12 dB and Q’s of 4. Although the frequency responses of the two filters will be identical, their phase responses can be very different.
You may occasionally hear the term minimum phase to describe a filter. This is a filter that has the frequency response that you want, and incurs the smallest (hence “minimum”) shift in phase to achieve that frequency response.
Two things to remember about minimum phase filters: 1) Just because they have the minimum possible phase shift doesn’t necessarily imply that they sound the best. 2) A minimum phase filter can be “undone” – that is to say that if you put your signal through a minimum phase filter, it is possible to find a second minimum phase filter that will reverse all the effects of the first, giving you exactly the signal you started with.
If you plot the phase response of a filter for all frequencies, chances are you’ll get a smooth, fancy-looking curve like the ones in Figure 6.18. Some filters, on the other hand, have a phase response plot that’s a straight line if you graph the response on a linear frequency scale (instead of a log scale like we normally do...). This line usually slopes upwards so the higher the frequency, the bigger the phase change. In fact, this would be exactly the phase response of a straight delay line – the higher the frequency, the more of a phase shift that’s incurred by a fixed delay time. If the delay time is 0, then the straight line is a horizontal one at 0∘ for all frequencies.
Any filter whose phase response is a straight line is called a linear phase filter. Be careful not to jump to the conclusion that, because it’s a linear phase filter, it’s better than anything else. While there are situations where such a filter is useful, they don’t necessarily work well in all situations to correct all problems. Different intentions require different filter characteristics.
The phase response of a filter is typically strongly related to its Q. The higher the Q (and therefore the smaller the bandwidth) the greater the change in phase around the centre frequency. This can be seen in Figure 6.18 above. Notice that, the higher the Q, the higher the slope of the phase response at the centre frequency of the filter. When the slope of the phase response of a filter gets very steep (in other words, when the Q of the filter is very high) an interesting thing called ringing happens. This is an effect where the filter starts to oscillate at its centre frequency for a length of time after the input signal stops. The higher the Q, the longer the filter will ring, and therefore the more audible the effect will be. In the extreme cases, if the Q of the filter is 0, then there is no ringing (but the bandwidth is infinity and you have a flat frequency response – so it’s not a very useful filter...). If the Q of the filter is infinity, then the filter becomes a sine wave generator.
All this information is great – but why and how would you use an equalizer?
This is probably the most obvious use for an equalizer. You have a lead vocal that sounds too bright so you want to cut back the high frequency content. Or you want to bump up the low mid range of a piano to warm it up a bit. This is the primary intention of the tone controls on the cheapest ghetto blaster through to the best equalizer in the recording studio. It’s virtually impossible to give a list of “tips and tricks” in this category, because every instrument and every microphone in every recording situation will be different. There are time when you’ll want to use an equalizer to compensate for deficiencies in the signal because you couldn’t afford a better mic for that particular gig. On the other hand there may be occasions where you have the most expensive microphone in the world on a particular instrument and it still needs a little tweaking to fix it up. There are, however, a couple of good rules to follow when you’re in this game.
First of all – don’t forget that you can use an equalizer to cut as well as boost. Consider a situation where you have a signal that has too much bass – there are two possible ways to correct the problem. You could increase the mids and highs to balance, or you could turn down the bass. There are as many situations where one of these is the correct answer as there are situations where the other answer is more appropriate. Try both unless you’re in a really big hurry.
Second of all – don’t touch the equalizer before you’ve heard what you’re tweaking. I often notice when I go to a restaurant that there are a huge number of people who put salt and pepper on their meal before they’ve even tasted a single morsel. Doesn’t make much sense... Hand them a plate full of salt and they’ll still shake salt on it before raising a hand to touch their fork. The same goes for equalization. Equalize to fix a problem that you can hear – not because you found a great EQ curve that worked great on kick drum at the last session.
Thirdly – don’t overdo it. Or at least, overdo it to see how it sounds when it’s overdone, then bring it back. Again, back to a restaurant analogy – you know that you’re in a restaurant that knows how to cook steak when there’s a disclaimer on the menu that says something to the effect of “We are not responsible for steaks ordered well done.” Everything in moderation – unless, of course, you’re intending to plow straight through the fields of moderation and into the barn of excess.
Fourthly, there’s a number of general descriptions that indicate problems that can be fixed, or at least tamed with equalization. For example, when someone says that the sound is “muddy,” you could probably clean this up by reducing the area around 125 – 250 Hz with a low-Q filter. Table 6.2 gives a number of basic examples, but there are plenty more – ask around...
| Symptom description | Possible remedy |
| Bright | Reduce high frequency shelf |
| Dark, veiled, covered | Increase high frequency shelf |
| Harsh, crunchy | Reduce 3 – 5 kHz region |
| Muddy, thick | Reduce 125 – 250 Hz region |
| Lacks body or warmth | Increase 250 – 500 Hz |
| Hollow | Reduce 500 Hz region |
One last trick here applies when you hear a resonant frequency sticking out, and you want to get rid of it, but you just don’t know what the exact frequency is. You know that you need to use a filter to reduce a frequency – but finding it is going to be the problem. The trick is to search and destroy by making the problem worse. Set a filter to boost instead of cutting a frequency band with a fairly high Q. Then, sweep the frequency of the filter until the resonance sticks out more than it normally does. You can then fine tune the centre frequency of the filter so that the problem is as bad as you can make it, then turn the boost back to a cut.
Although we rarely like to admit it, we humans aren’t perfect. This is true in many respects, but for the purposes of this discussion, we’ll concentrate specifically on our abilities to hear things. Unfortunately, our ears don’t have the same frequency response at all listening levels. At very high listening levels, we have a relatively flat frequency response, but as the level drops, so does our sensitivity to high and low frequencies. (This effect was discussed in Section 5.4.) As a result, if you mix a tune at a very high listening level and then reduce the level, it will appear to lack low end and high end. Similarly, if you mix at a low level and turn it up, you’ll tend to hear more low end and high end.
One possible use for an equalizer is to compensate for the perceived lack of information in extreme frequency ranges at low listening levels. Essentially, when you turn down the monitor levels, you can use an equalizer to increase the levels of the low and high frequency content to compensate for deficiencies in the human hearing mechanism. This filtering is identical to that which is engaged when you press the “loudness” button on most home stereo systems. Of course, the danger with such equalization is that you don’t know what frequency ranges to alter, and how much to alter them – so it is not recommendable to do such compensation when you’re mixing, only when you’re at home listening to something that’s already been mixed.
It’s possible in some specific cases to use equalization to reduce noise in recordings, but you have to be aware of the damage that you’re inflicting on some other parts of the signal.
High-frequency Noise (Hiss)
Let’s say that you’ve got a recording of an electric bass on a really noisy analog tape deck. Since most of the perceivable noise is going to be high-frequency stuff and since most of the signal that you’re interested in is going to be low-frequency stuff, all you need to do is to roll off the high end to reduce the noise. Of course, this is be best of all possible worlds. It’s more likely that you’re going to be coping with a signal that has some high-frequency content (like your lead vocals, for example...) so if you start rolling off the high end too much, you start losing a lot of brightness and sparkle from your signal, possibly making the end result worse that you started. If you’re using equalization to reduce noise levels, don’t forget to occasionally hit the “bypass” switch of the equalizer once and a while to hear the original. You may find when you refresh your memory that you’ve gone a little too far in your attempts to make things better.
Low-frequency Noise (Rumble)
Almost every console in the world has a little button on every input strip that has a symbol that looks like a little ramp with the slope on the left. This is a high-pass filter that is typically a second-order filter with a cutoff frequency around 100 Hz or so, depending on the manufacturer and the year it was built. The reason that filter is there is to help the recording or sound reinforcement engineer get rid of low-frequency noise like “stage rumble” or microphone handling noise. In actual fact, this filter won’t eliminate all of your problems, but it will certainly reduce them. Remember that most signals don’t go below 100 Hz (this is about an octave and a half below middle C on a piano) so you probably don’t need everything that comes from the microphone in this frequency range – in fact, chances are, unless you’re recording pipe organ, electric bass or space shuttle launches, you won’t need nearly as much as you think below 100 Hz.
Hummmmmmm...
There are many reasons, forgivable and unforgivable, why you may wind up with an unwanted hum in your recording. Perhaps you work with a poorly-installed system. Perhaps your recording took place under a buzzing streetlamp. Whatever the reason, you get a single frequency (and perhaps a number of its harmonics) singing all the way through your recording. The nice thing about this situation is that, most of the time, the hum is at a predictable frequency (depending on where you live, it’s likely a multiple of either 50 Hz or 60 Hz) and that frequency never changes. Therefore, in order to reduce, or even eliminate this hum, you need a very narrow band-reject filter with a lot of attenuation. Just the sort of job for a notch filter. The drawback is that you also attenuate any of the music that happens to be at or very near the notch centre frequency, so you may have to reach a compromise between eliminating the hum and having too detrimental of an effect on your signal.
A dynamic equalizer is one which automatically changes its frequency response according to characteristics of the signal passing through it. You won’t find many single devices what fit this description, but you can create a system that behaves differently for different input signals if you add a compressor to the rack. This is easily accomplished today with digital multi-band compressors which have multiple compressors fed by what could be considered a crossover network similar to that used in loudspeakers.
Dynamic enhancement
Take your signal and, using filters, divide it into two bands with a crossover frequency at around 5 kHz. Compress the higher band using a fast attack and release time, and adjust the output level of the compressor so that when the signal is at a peak level, the output of the compressor summed with the lower frequency band results in a flat frequency response. When the signal level drops, the low frequency band will be reduced more than the high frequency band and a form of high-frequency enhancement will result.
Dynamic Presence
In order to add a sensation of “presence” to the signal, use the technique described in Section 6.1.5 but compress the frequency band in the 2 kHz to 5 kHz range instead of all high frequencies.
There are many instances where a close-mic technique is used to record a narrator and the result is a signal that emphasizes the sibilant material in the signal – in particular the “s” sound. Since the problem is due to an excess of high frequency, one option to fix the issue could be to simply roll off high frequency content using a low-pass filter or a high-frequency shelf. However, this will have the effect of dulling all other material in the speech, removing not only the “s’s” but all brightness in the signal. The goal, therefore, is to reduce the gain of the signal when the letter “s” is spoken. This can be accomplished using an equalizer and a compressor with a side chain. In this case, the input signal is routed to the inputs of the equalizer and the compressor in parallel. The equalizer is set to boost high frequencies (thus making the “s’s” even louder...) and its output is fed to the side chain input of the compressor. The compression parameters are then set so that the signal is not normally compressed, however, when the “s” is spoken, the higher output level from the equalizer in the side chain triggers compression on the signal. The output of the compressor has therefore been “de-essed” or reduced in sibilance.
Although it seems counterintuitive, don’t forget that, in order to reduce the level of the high frequencies in the output of the compressor, you have to increase the level of the high frequencies at the output of the equalizer in this case.
Pop-reduction
A similar problem to de-essing is the “pop” that occurs when a singer’s plosive sounds (p’s and b’s) cause a thump at the diaphragm of the microphone. There is a resulting overload in the low frequency component of the signal that can be eliminated using the same technique described in Section 6.1.5 where the low frequencies (250 Hz and below) are boosted in the equalizer instead of the high frequency components.
We saw above that the quality factor, or Q, is defined by the centre frequency and the bandwidth of the filter. That bandwidth is defined using the two cutoff frequencies of the filter’s response, which are, in turn, defined using a -3 dB point. So, to find the cutoff frequencies, you find the peak in the filter’s response, and then go 3 dB below that and find the frequencies that intersect that level.
However, this results in some strange effects as we saw above. If you have a peaking filter, then your cutoff frequencies are 3 dB below the peak – the maximum effect in your gain. However, if you have a notch filter, then your -3 dB point is measured down from the part of the response that is unaffected. This is why a constant-Q peak/dip filter is asymmetrical. If you want to make a reciprocal peak/dip filter, you have to change your definition a little so that, if you’re applying a dip, then you measure the bandwidth using the points that at 3 dB up from the bottom of the dip, so we’re not really following the definition of bandwidth (or Q) properly.
Another problem arises when you have a peak gain that is less than 3 dB. Let’s say that you use a reciprocal peak/dip filter to apply a gain of 2 dB. This means that no point in the response is 3 dB lower than the peak, so it therefore has no definable bandwidth or Q? Hmmmmm.....
There have been some suggested solutions to these problems that have become commonplace in the gear that we use every day. As a result, if you’re really picky about what you’re doing, you should be aware of the variations on Q.
As we saw above, if the Q and bandwidth are always defined by the -3 dB point, then you result in a constant Q behaviour in a peak/dip filter, and therefore an asymmetrical behaviour.
The simplest solution to this problem of asymmetry is to re-define bandwidth when you have a dip – therefore using the 3 dB up points instead.
However, both this method, and the Constant Q method suffer from the problem of what the bandwidth and Q are when the gain is greater than -3 dB and less than 3 dB (since you can’t find a point in a magnitude response that’s 3 dB down when the highest peak is less than 3 dB up...).
One solution that was offered [Moorer, 1983] to get around the problem of gains below 6 dB was to re-define the bandwidth so that, whenever the peak gain is less than 6 dB, you use the gain value that is half of the peak value. For example, if the gain is 6 dB, then you define your bandwidth using the point 3 dB down from that (half of 6 is 3). If the gain is 4 dB, then you define bandwidth using the 2 dB-down (relative to the peak) point.
The nice thing about this definition is that, by using half of the gain to define the bandwidth (and therefore the Q) you automatically get a reciprocal (and therefore symmetrical) shape for peaks and dips.
Finally, along came a guy named Robert Bristow-Johnson who suggested that, since using the half-gain point to define Q was so useful (particularly in making reciprocal filters) then we should use it all the time[Bristow-Johnson, 1994].
There are two catches here. The first is that he suggested that we use this new definition not only for peak/dip filters, but shelving filters as well. The second is that he put a set of equations on Usenet (a precursor to the World Wide Web - where they live today at http://www.musicdsp.org/files/Audio-EQ-Cookbook.txt) that are used to implement the filters. Since those equations were freely available, everyone (well, almost everyone) uses them when they’re building the equalisers that you use in the gear that you buy.
Well... the big question here is whether or not you care that these differences exist. Maybe not. Personally, I do... however, it’s for a very good reason. If I implement an EQ curve on one piece of gear and write down my parameters (type, centre or cutoff frequency, gain and Q) I expect to be able to put those parameters in another piece of gear and get exactly the same response out. This won’t happen if the people who made your equalisers use different definitions of Q. This might be very bad... How bad? Well, let’s take a look...
Changes in gain
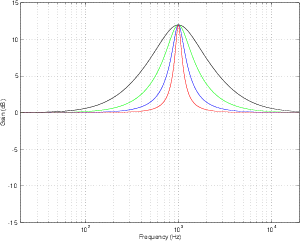
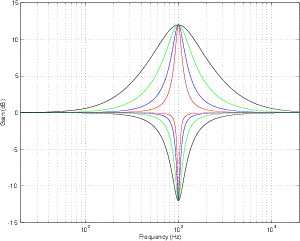
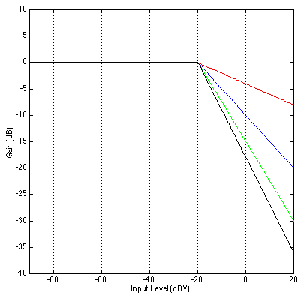
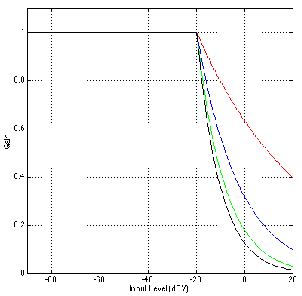
Figures 6.21 and 6.22 shows the difference in gain and phase respectively between two filters, both with an fc of 1 kHz and a Q of 2 and three different gains. However, one filter calculates Q based on the 3 dB down point, the other based on the midpoint of the maximum gain.
Changes in Q
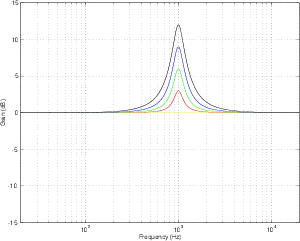
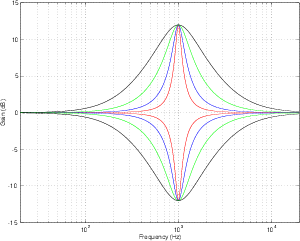
Figures 6.23 and 6.24 shows the difference in gain and phase respectively between two filters, both with an fc of 1 kHz and a gain of 12 dB and five different Q’s. Again, one filter calculates Q based on the 3 dB down point, the other based on the midpoint of the maximum gain.
What is a filter? – from Julius O. Smith’s substantial website.
So you’re out for a drive in your car, listening to some classical music played by an orchestra on your car’s CD player. The piece starts off very quietly, so you turn up the volume because you really love this part of the piece and you want to hear it over the noise of your engine. Then, as the music goes on, it gets louder and louder because that’s what the composer wanted. The problem is that you’ve got the stereo turned up to hear the quiet sections, so these new loud sections are really loud – so you turn down your stereo. Then, the piece gets quiet again, so you turn up the stereo to compensate.
What you are doing is to manipulate something called the “dynamic range” of the piece. In this case, the dynamic range is the difference in level between the softest and the loudest parts of the piece (assuming that you’re not mucking about with the volume knob). By fiddling with your stereo, you’re making the soft sounds louder and the loud sounds softer, and therefore compressing the dynamics. The music still appears to have quiet sections and loud sections, but they’re not as different as they were without your fiddling.
In essence, this is what a compressor does – at the most basic level, it makes loud sounds softer and soft sounds louder so that the music going through it has a smaller (or compressed) dynamic range. Of course, I’m oversimplifying, but we’ll straighten that out.
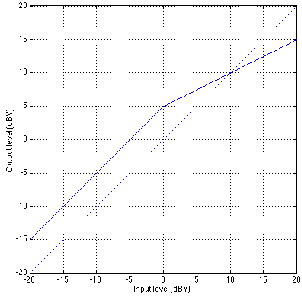
Let’s look at the gain response of an ideal piece of wire. This can be shown as a transfer function as seen in Figure 6.25.
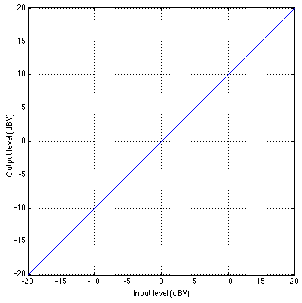
Now, let’s look at the gain response for a simple device that behaves as an oversimplified compressor. Let’s say that, for a sine wave coming in at 0 dBV (1 Vrms, remember?) the device has a gain of 1 (or output=input). Let’s also say that, for every 2 dB increase in level at the input, the gain of this device is reduced by 1 dB – so, if the input level goes up by 2 dB, the output only goes up by 1 dB (because it’s been reduced by 1 dB, right?) Also, if the level at the input goes down by 2 dB, the gain of the device comes up by 1 dB, so a 2 dB drop in level at the input only results in a 1 dB drop in level at the output. This generally makes the soft sounds louder than when they went in, the loud sounds softer than when they went in, and anything at 0 dBV come out at exactly the same level as it goes in.
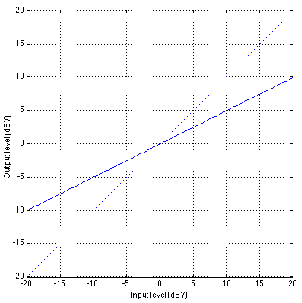
If we compare the change in level at the input to the change in level at the output, we have a comparison between the original dynamic range and the new one. This comparison is expressed as a ratio of the change in input level in decibels to change in output level in decibels. So, if the output level goes up 1 dB for every 2 dB increase in level at the input, then we have a 2:1 compression ratio. The higher the compression ratio, the more the dynamic range is reduced.
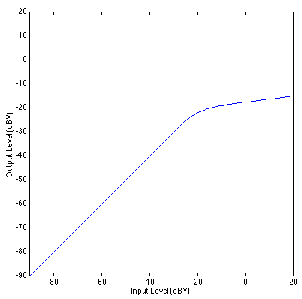
Notice in Figure 6.26 that there is one input level (in this case, 0 dBV) that results in a gain of 1 – that is to say that the output is equal to the input. That input level is known as the rotation point of the compressor. The reason for this name isn’t immediately obvious in Figure 6.26, but if we take a look at a number of different compression ratios plotted on the same graph as in Figure 3, then the reason becomes clear.
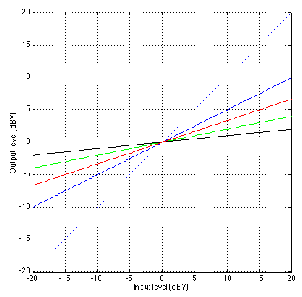
Normally, a compressor doesn’t really behave in the way that’s seen in any of the above diagrams. If we go back to thinking about listening to the stereo in the car, we actually leave the volume knob alone most of the time, and only turn it down during the really loud parts. This is the way we want the compressor to behave. We’d like to leave the gain at one level (let’s say, at 1) for most of the program material, but if things get really loud, we’ll start turning down the gain to avoid letting things get out of hand. The gain response of such a device is shown in Figure 6.28.

The level where we change from being a linear gain device (meaning that the gain of the device is the same for all input levels) to being a compressor is called the threshold. Below the threshold, the device applies the same gain to all signal levels. Above the threhold, the device changes its gain according to the input level. This sudden bend in the transfer function at the threshold is called the knee in the response.
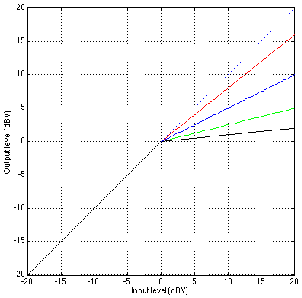
In the case of the plot shown in Figure 6.28, the rotation point of the compressor is the same as the threshold. This is not necessarily the case, however. If we look at Figure 6.29, we can see an example of a curve where this is illustrated.
This device applies a gain of 5 dB to all signals below the threshold, so an input level of -20 dBV results in an output of -15 dBV and an input at -10 dBV results in an output of -5 dBV. Notice that the threshold is still at 0 dBV (because it is the input level over which the device changes its behaviour). However, now the rotation point is at 10 dBV.
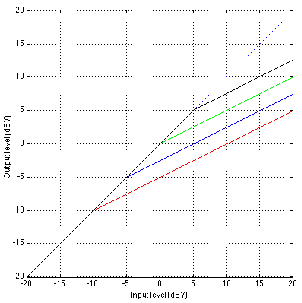
Let’s look at an example of a compressor with a gain of 1 below threshold, a threshold at 0 dBV and different compression ratios. The various curves for such a device are shown in Figure 6.30. Notice that, below the threshold, there is no difference in any of the curves. Above the threshold, however, the various compression ratios result in very different behaviours.
There are two basic “styles” in compressor design when it comes to the threshold. Some manufacturers like to give the user control over the threshold level itself, allowing them to change the level at which the compressor “kicks in.” This type of compressor typically has a unity gain below threshold, although this isn’t always the case. Take a look at Figure 6.31. This shows a number of curves for a device with a compression ratio of 2:1, unity gain below threshold and an adjustable threshold level.
The advantage of this design is that the bulk of the signal, which is typically below the threshold, remains unchanged – by changing the threshold level, we’re simply changing the level at which we start compressing. This makes the device fairly intuitive to use, but not necessarily a good design for the final sound quality.
Let’s think about the response of this device (with a 2:1 compression ratio). If the threshold is turned up to 12 dBV, then any signal coming in that’s less than 12 dBV will go out unchanged. If the input signal has a level of 20 dBV, then the output will be 16 dBV, because the input went 8 dB above threshold and the compression ratio is 2:1, so the output goes up 4 dB.
If the threshold is turned down to -12 dBV, then any signal coming in that’s less than -12 dBV will go out unchanged. If the input signal has a level of 20 dBV, then the output will be 4 dBV, because the input went 32 dB above threshold and the compression ratio is 2:1, so the output goes up 16 dB.
So what? Well, as you can see from Figure 6.31, changing the compression ratio will affect the output level of the loud stuff by an amount that’s determined by the relationship between the threshold and the compression ratio.
Consider for a moment how a compressor will be used in a recording situation: we use the compressor to reduce the dynamic range of the louder parts of the signal. As a result, we can increase the overall level of the output of the compressor before going to tape. This is because the spikes in the signal are less scary and we can therefore get closer to the maximum input level of the recording device. As a result, when we compress, we typically have a tendency to increase the input level of the device that follows the compressor. Don’t forget, however, that the compressor itself is adding noise to the signal, so when we boost the input of the next device in the audio chain, we’re increasing not only the noise of the signal itself, but the noise of the compressor as well. How can we reduce or eliminate this problem? Use compressor design philosophy number 2...
Instead of giving the user control over the threshold, some compressor designers opt to have a fixed threshold and a variable gain before compression. This has a slightly different effect on the signal.
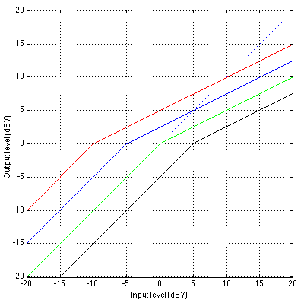
Let’s look at the implications of this configuration using the response in Figure 6.32 which has a fixed threshold of 0 dBV. If we look at the green curve with a gain of 0 dB, then signals coming in are not amplified or attenuated before hitting the threshold detector. Therefore, signals lower than 0 dBV at the input will be unaffected by the device (because they aren’t being compressed and the gain is 0 dB). Signals greater than 0 dBV will be compressed at a 2:1 compression ratio.
Now, let’s look at the blue curve. The low-level signals have a constant 5 dB gain applied to them – therefore a signal coming in a -20 dBV comes out at -15 dBV. An input level of -15 dBV results in an output of -10 dBV. If the input level is -5 dBV, a gain of 5 dB is applied and the result of the signal hitting the threshold detector is 0 dBV – the level of the threshold. Signals above this -5 dBV level (at the input) will be compressed.
If we just consider things in the theoretical world, applying a 5 dB gain before compression (with a threshold fixed at 0 dBV) results in the same signal that we’d get if we didn’t change the gain before compression, reduced the threshold to -5 dBV and then raised the output gain of the compressor by 5 dB. In the practical world, however, we are reducing our noise level by applying the gain before compression, since we aren’t amplifying the noise of the compressor itself.
There’s at least one manufacturer that takes this idea one step further. Let’s say that you have the output of a compressor being sent to the input of a recording device. If the compressor has a variable threshold and you’re looking at the record levels, then the more you turn down the threshold, the lower the signal going into the recording device gets. This can be seen by looking at the graph in Figure 6.31 comparing the output levels of an input signal with a level of 20 dBV. Therefore, the more we turn down the threshold on the compressor, the more we’re going to turn up the input level on the recorder.
Take the same situation but use a compressor with a variable gain before compression. In this case, the more we turn up the gain before compression, the higher the output is going to get. Now, if we turn up the gain before compression, we are going to turn down the input level to the recorder to make sure that things don’t get out of hand.
What would be nice is to have a system where all this gain compensation is done for you. So, using the example of a compressor with gain before compression: we turn up the gain before compression by some amount, but at the same time, the compressor turns down its output to make sure that the compressed part of the signal doesn’t get any louder. In the case where the compression ratio is 2:1, if we turn up the gain before compression by 10 dB, then the output has to be turned down by 5 dB to make this happen. The output attenuation in dB is equal to the gain before compression (in dB) divided by the compression ratio.
What would this response look like? It’s shown in Figure 6.33. As you can see, changes in the gain before compression are compensated so that the output for a signal above the threshold is always the same, so we don’t have to fiddle with the input level of the next device in the chain.
If we were to do the same thing using a compressor with a variable threshold, then we’d have to boost the signal at the output, thus increasing the apparent noise floor of the compressor and making it sound as bad as it is...
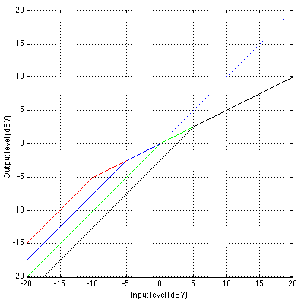
As you can see from Figure 6.33, the advantage of this system is that adjustments in the gain before compression (or the threshold) don’t have any affect on how the loud stuff behaves – if you’re past the threshold, you get the same output for the same input.
So far we’ve been looking at the relationship between the output level and the input level of a compressor. Let’s look at this relationship in a different way by considering the gain of the compressor for various signals.
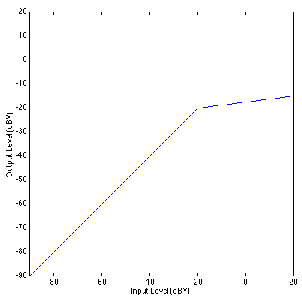
Figure 6.34 shows the level of the output of a compressor with a given threshold and compression ratio. As we would expect, below the threshold, the output is the same as the input, therefore the gain for input signals with a level of less than -20 dBV in this case is 0 dB – unity gain. For signals above this threshold, the higher the level gets the more the compressor reduces the gain – in fact, in this case, for every 8 dB increase in the input level, the output increases by only 1 dB, therefore the compressor reduces its gain by 7 dB for every 8 dB increase. If we look at this gain vs. the input level, we have a response that is shown in Figure 6.35.

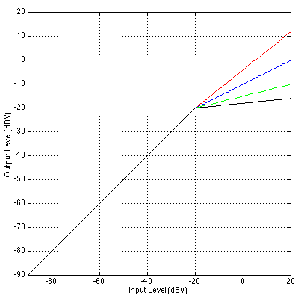
Notice that Figure 6.35 plots the gain in decibels vs. the input level in dBV. The result of this comparison is that the gain reduction above the threshold appears to be a linear change with an increase in level. This response could be plotted somewhat differently as is shown in Figure 6.36.
You’ll now notice that there is a rather dramatic change in gain just above the threshold for signals that increase in level just a bit. The result of this is an audible gain change for signals that hover around the threshold – an artifact called pumping This is an issue that we’ll deal with a little later.
Let’s now consider this same issue for a number of different compression ratios. Figures 6.37, 6.38 and 6.39 show the relationships of 4 different compression ratios with the same thresholds and gains before compression to give you an idea of the change in the gain of the compressor for various ratios.
There is a simple solution to the problem of the pumping caused by the sudden change in gain when the signal level crosses the threshold. Since the problem is caused by the fact that the gain change is sudden because the knee in the response curve is a sharp corner, the solution is to soften the sharp corner into a gradual bend. This response is called a soft knee for obvious reasons as can be seen in Figure 6.40.
So far, we’ve been looking at a device that alters its gain according to the input level, but we’ve been talking in terms of the input level being measured in dBV – therefore, we’re thinking of the signal level in VRMS. In fact, there are two types of level detection available – compressors can either respond to the RMS value of the input signal, or the peak value of the input signal. In fact, some compressors give you the option of selecting some combination of the two instead of just selecting one or the other.
Probably the simplest signal detection method is the RMS option. As we’ll see later, the signal that is input to the device goes to two circuits: one is the circuit that changes the gain of the signal and sends it out the output of the device. The second, known as the control path determines the RMS level of the signal and outputs a control signal that changes the gain of the first circuit. In this case, the speed at which the control circuit can respond to changes in level depends on the time constant of the RMS detector built into it. For more info on time constants of RMS measurements, see Section 2.1.6. The thing to remember is that an RMS measurement is an average of the signal over a given period of time, therefore the detection system needs a little time to respond to the change in the signal. Also, remember that if the time constant of the RMS detection is long, then a short, high level transient will get through the system without it even knowing that it happened.
If you’d like your compressor to respond a little more quickly to the changes in signal level, you can typically choose to have it determine its gain based on the peak level of the signal rather than the RMS value. In reality, the compressor is not continuously looking at the instantaneous level of the voltage at the input – it’s usually got a circuit built in that looks at a smoothed version of the absolute value of the signal. Almost all compressors these days give you the option to switch between a peak and an RMS detection circuit.
On high-end units, you can have your detection circuit respond to some mix of the simultaneous peak and RMS values of the input level. Remember from Chapter 2.1.6 that the ratio of the peak to the RMS is called the crest factor. This ratio of peak/RMS can either be written as a value from 0 to something big, or it may be converted into a dB scale. Remember that, if the crest factor is near 0 (or -∞ dB), then the RMS value is much greater than the peak value and therefore the compressor is responding to the RMS of the signal level. If the crest factor is a big number, then the compressor is responding to the peak value of the input level.
Now that we’re talking about the RMS and the smoothed peak of the signal, we have to start considering what time it is. Up to now, we’ve been only looking at the output level or the gain of the compressor based on a static input level. We have been assuming that the only thing we’re sending through the unit is a steady-state sine tone. Of course, this is pretty boring to listen to, but if we’re going to look at real-world signals, then the behaviour of the compressor gets pretty complicated.
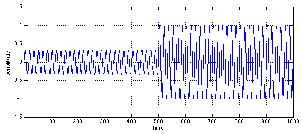
Let’s start by considering a signal that’s quiet to begin with and suddenly gets louder. For the purposes of this discussion, we’ll simulate this with a pulse-modulated sine wave like the one shown in Figure 6.41.
Unfortunately, a real-world compressor cannot respond instantaneously to this sudden change in level. In order to be able to do this, the unit would have to be able to see into the future to know what the new peak value of the signal will be before we actually hit that peak. (In fact, some digital compressors can do this by delaying the signal and turning the present into the past and the future into the present, but we’ll pretend that this isn’t happening for now...).
Let’s say that we have a compressor with a gain before compression of 0 dB and a threshold that’s set to a level that’s higher than the lower-level signal in Figure 6.41, but lower than the higher-level signal. So, the first part of the signal, the quiet part, won’t be compressed and the later, louder part will. Therefore the compressor will have to have a gain of 1 (or 0 dB) for the quiet signal and then a reduced gain for the louder signal.
Since the compressor can’t see into the future, it will respond somewhat slowly to the sudden change in level. In fact, most compressors allow you to control the speed with which the gain change happens. This is called the attack time of the compressor. Looking at Figure 6.42, we can see that the compressor has a sudden awareness of the new level (at Time = 500) but it then settles gradually to the new gain for the higher signal level. This raises a question – the gain starts changing at a known time, but, as you can see in Figure 6.42, it approaches the final gain forever without really reaching it. The question that’s raised is “what is the time of the attack time?” In other words, if I say that the compressor has an attack time of 200 ms, then what is the relationship between that amount of time and the gain applied by the compressor. The answer to this question is found in the chapter on capacitors. Remember that, in a simple RC circuit, the capacitor charges to a new voltage level at a rate determined by the time constant which is the product of the resistance and the capacitance. After 1 time constant, the capacitor has charged to 63 % of the voltage being applied to the circuit. After 5 time constants, the capacitor has charged to over 99 % of the voltage, and we consider it to have reached its destination. The same numbers apply to compressors. In the case of an attack time of 200 ms, then after 200 ms has passed, the gain of the compressor will be at 63 % of the final gain level. After 5 times the attack time (in this case, 1 second) we can consider the device to have reached its final gain level. (In fact, it never reaches it, it just gets closer and closer and closer forever...)
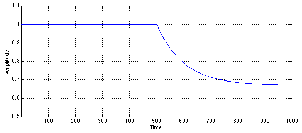
What is the result of the attack time on the output of the compressor? This actually is pretty interesting. Take a look at Figure 6.43 showing the output of a compressor that has the signal in Figure 6.41 sent into it and responding with the gain in Figure 6.42. Notice that the lower-level signal goes out exactly as it went it. We would expect this because the gain of the compressor for that portion of the signal is 1. Then the signal suddenly increases to a new level. Since the compressor detection circuit take a little while to figure out that the signal has gotten louder, the initial new loud signal gets through, almost unchanged. As we get further and further into the new level in time, however, the gain settles to the new value and the signal is compressed as we would expect. The interesting thing to note here is that a portion of the high-level signal gets through the compressor. The result is that we’ve created a signal that sounds like more of a transient than the input. This is somewhat contrary to the way most people tend to think that a compressor behaves. The common belief is that a compressor will control all of your high-level signals, thus reducing your dynamic range – but this is not exactly the case as we can see in this example. In fact, it may be possible that the perceived dynamic range is greater than the original because of the accents on the transient material in the signal.
Similarly, what happens when the signals decreases in level from one that is being compressed to one that is lower than the threshold? Again, it takes some time for the compressor’s detection circuit to realize that the level has changed and therefore responds slowly to fast changes. This response time is called the release time of the compressor. (Note that the release time is measured in the same way as the attack time – it’s the amount of time it takes the compressor to get to 63% of its intended gain.)
For example, we’ll assume that the signal in Figure 6.44 is being fed into a compressor. We’ll also assume that the higher-level signal is above the compression threshold and the lower-level signal is lower than the threshold.
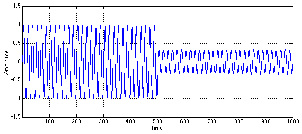
This signal will result in a gain reduction for the first part of the signal and no gain reduction for the latter part, however, the release time of the compressor results in a transition time from these two states as is shown in Figure 6.45.
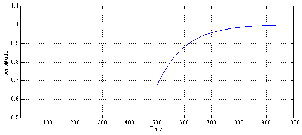
Again, the result of this gain response curve is somewhat interesting. The output of the compressor will start with a gain-reduced version of the louder signal. When the signal drops to the lower level, however, the compressor is still reducing the gain for a while, therefore we wind up with a compressed signal that’s below the threshold – a signal that normally wouldn’t be compressed. As the compressor figures out that the signal has dropped, it releases its gain to return to a unity gain, resulting in an output signal shown in Figure 6.46.
Just for comparison purposes, Figures 6.47 and 6.48 show a number of different attack and release times.
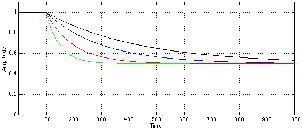
One last thing to discuss is a small issue in low-cost RMS-based compressors. In these machines, the attack and release times of the compressor are determined by the time constant of the RMS detection circuit. Therefore, the attack and release times are identical (normally, we call them “symmetrical”) and not adjustable. Check your manual to see if, by going into RMS mode, you’re defeating the attack time and release time controls.
On its simplest level, a compressor can be thought of as a device which controls its gain based on the incoming signal. In order to do this, it takes the incoming audio and sends it in two directions, along the audio path, which is where the signal goes in, gets modified and comes out the output; and the control path, (also known as a side chain) where the signal comes in, gets analysed and converted into a different signal which is used to control the gain of the audio path.
As a result, we can think of a basic compressor as is shown in the block diagram in Figure 6.49.
If we’re going to start asking difficult questions about compressors, a good place to start is to look at the the behaviour of the level detection component of the side chain. Exactly what kind of level is the level detection measuring (or at least, claiming to measure...), how accurate is that measurement, and how well does it behave?
There are a number of possible answers to the first part of the question. Depending on the compressor, you might have one with an RMS detector, a peak detector (probably with an RC-based attack and release control) or a pseudo-RMS detector. Let’s look at how each of these behaves, how they behave differently, and how neither of them will give you what you expect or want...
Let’s start by looking at a very simple signal. We will make a stepped signal that goes from 0 V 1 to 0.5 V to 1 V, back down to 0.5 V and returning to (almost) 0 V. This input signal is shown as the green line in Figures 6.50 to 6.57.
RMS Detectors
Figures 6.50 and 6.51 show the response of a running RMS measurement of the signal. There are at least four things to notice here. Firstly, when the input voltage changes, the RMS measurement is always a little late getting to the new value. (To be precise, the amount of time it takes to get to the new voltage is equal to the RMS time window.) Secondly, the shapes of the attack and the decay of the RMS detector output are symmetrical. Thirdly, there are two discontinuities in the slope of the RMS detector output signal on each change of input voltage. (In other words, there are two “corners” in the black line for every jump in the green line.) Fourthly, because this is a DC signal (between changes, at least...) the RMS output is equal to the input after the detector has settled. This would not be true if the input voltage was changing faster than one RMS time constant apart. If that were the case, then the RMS detector would not have time to get to the new input voltage before it had to go somewhere else. Later, we’ll see that this is a problem with more musical signals like sine waves.
Pseudo RMS Detectors
Some manufacturers don’t like implementing true RMS detection in their compressors because it’s expensive. If you’re working with analogue gear, it means you have to put in more parts. If you’re building a digital compressor, then you need more memory. Either way, if you can get a nearly-RMS behaviour without the added expense, you might try to get away with this. One easy way to do this is to keep the R and the S and throw away the M in the RMS. In other words, you Square the input signal, then low-pass filter the result with a first-order RC filter (instead of finding the Mean value), and get the square Root of the result. If you’re reasonably careful about your RC time constant (in other words, the cutoff frequency of your low-pass filter), then you can get something that behaves something like an RMS detector without the expense.
However, what you get will not be exactly like an RMS detector as we can see in Figures 6.52 and 6.53.
Note that there is a small difference in the ramp-up behaviour as compared to a true-RMS detector. Specifically, there is only one discontinuity in the signal’s slope (only one corner in the black line). Other than that, it appears to be almost the same shape. However, the ramp-down behaviour is very different. If you look at the shape of the curve in Figure 6.52 compared to Figure 6.50, you can see that they have sort of an opposite behaviour in time. Where the RMS detector has a an increasingly vertical slope as it goes through its decay, the pseudo-RMS detector starts with a nearly-vertical slope and becomes more and more horizontal at it reaches its target value. This difference is even more evident when you take a look at the same curves displayed on a decibel scale. (see Figures 6.51 and 6.53.) The RMS detector’s output has an increasingly vertical decay when measured in decibels (therefore the rate of change in dB increases over time) whereas the pseudo-RMS detector’s output has a constant slope in dB over time. (This means that the decay of the pseudo-RMS detector’s output is more like the decay of a musical instrument or a reverb tail.)
Peak Detector with Symmetrical RC-based Attack and Release
In other cases, a compressor will be based on a peak detection circuit which is typically followed by a first-order RC circuit to control the attack and release times. In this case, the absolute value of the incoming signal is low-pass filtered by the first-order low-pass filter. Usually there are two different filters - one for attack and the other for the release. However, we’ll look at a system with a single low-pass first. Figures 6.54 and 6.55 show the output of a peak detector with a single RC filter used to smooth its output.
Note that the behaviour of this circuit is very similar to that of the pseudo-RMS detection circuit. In fact, if you don’t look carefully, you’ll think that the two curves are identical. However, they’re not – looking carefully, you’ll see that the response of the peak detector with the symmetrical RC low-pass is faster than that of the pseudo-RMS detector. This is particularly noticeable in the decibel scale representations of the responses in Figures 6.55 and 6.53. This is due to the fact that, in the case of the pseudo-RMS detector, the RC circuit is applied to the square of the signal (analogous to the signal’s power) whereas, in the case of the peak detector, the RC circuit is applied to the absolute value of the signal. This means, that, in the case of the pseudo-RMS detector, we’re seeing the square root of the response of the RC filter, whereas in the case of the peak detector, we see the unaltered response of the RC filter.
Peak Detector with Asymmetrical Attack and Release
Of course, it is more normal with a peak compressor to have separate attack and release time controls. While this will typically be implemented in almost exactly the same way as the previously-described circuit with a symmetrical attack and release, the usual setting of fast-attack-with-a-slow-release may result in an effect of this circuit to be seen more often. Figures 6.56 and 6.57 show a peak detector with separate RC smoothing filters for the attack and the release. The attack filter (when the input signal is increasing) is set to have a time constant of 0.2 ms, identical to the symmetrical filter shown above. The release filter (when the input signal is decreasing) is set to have a time constant of 100 times the attack. Note that these values should not be taken as suggestions – they are merely arbitrary values chosen to illustrate the behaviour of the detection circuit.
As can be seen in Figures 6.56 and 6.57, the attack of the detection circuit is identical to the symmetrical behaviour shown in Figures 6.54 and 6.55. This is because the two circuits are, in fact identical. However, as is immediately obvious in both Figure 6.56 and Figure 6.57, the release takes much longer to decay. This should not come as a surprise. However, the interesting thing to note is the change in slope at 35 ms. This is caused by the fact that the target value (the input voltage) changes at 35 ms, before the decay from the change at 25 ms has settled.
Sine waves
Let’s now move away from a simple input signal (the stepped DC used above) to something a little more complicated like a sine wave. This makes the detectors a little more busy, since they’re always trying to catch up to an ever-changing input level. Now the behaviour of the detectors’ outputs will be highly dependent on the relationship between the input signal’s period and the time constant of the detectors’ smoothing filters.
When the period of the input signal is much longer than the detector’s time constant, the level detector will have an output that is very similar to the absolute value of the input signal. This can be seen in the example in Figure 6.58. As can be seen in this example, nearly all of the detectors’ outputs are equivalent, the exception being the Peak Detector with the asymmetrical attack and release, since its release time constant is 20 ms – two times the period of the incoming signal. In the other three cases, it can be seen that the output of the detectors swings back and forth from nearly 0 V up to a value very close to the peak value of the input signal. We can think of this deviation as a ripple in the outputs of the detectors. So, we can say that, when the period of the input signal is much greater than the time constant of the detector’s smoothing filter, the peak-to-peak ripple on the output of the detector is close to the peak amplitude of the input signal.
In addition, you can see that the outputs of all level detectors is slightly behind the input signal – some more than others.
As the period of the input signal decreases and approaches the time constant of the level detector, the ripple on the output of the detector will decrease. An example of this is shown in Figure 6.59. In almost all cases shown in this plot, the ripple follows the envelope of the absolute value of the signal, however, in all cases, that ripple has a much smaller peak-to-peak amplitude than we saw in the case of the 100 Hz input.
You may notice that there is an exception. After it has stabilised following the initial start of the sine wave, the RMS detector has no ripple. This is because the period of the input signal is equal to the RMS time window in this example. (In fact, as we’ll see later, this will happen at other specific frequencies – whenever the RMS time window is exactly equal to 0.5 periods, 1 period, 1.5 periods, 2 periods, and so on...)
When the period of the input signal is much shorter than the time constant of the smoothing filter of the detector, the ripple of the detectors becomes even smaller, and their attack behaviour at the onset of the input sine wave is more similar to the attack behaviour with a stepped DC signal. This can be seen in Figure 6.60
Figures 6.61, 6.62 and 6.63 are included to show the release behaviour of the various detectors at the end of the same sine wave inputs. Note in Figure 6.61 that, like the signal itself, the RMS detector has a corner in its output when it reaches 0, whereas the other detectors have a smooth transition to 0.
In Figure 6.62 we can see that the release envelope of the RMS detector is exactly symmetrical to the attack envelope (shown in Figure 6.59). In fact, this is true for other frequencies – it’s just easier to see here...
Again in Figure 6.63 we can see that, at very high frequencies when the signal’s period is much shorter than the detector’s smoothing filter’s time constant, the release behaviour of the various detectors is very similar to that seen in the case of an input signal made with a stepped DC.
Now that we’ve seen some examples of the ripple of the output of the various level detectors at three frequencies, we can look at the magnitude of the ripple across a wider frequency range. Figure 6.64 shows the minimum and maximum output levels from the four detectors we’ve been looking at previously. The input signal is a sine wave with a peak amplitude of 1. The RMS time window is 1 ms. The RC time constant of the low pass filters used in the pseudo-RMS detector, the peak detector with the symmetrical attack and release, and the attack of the asymmetrical peak detector is 0.2 ms. The RC time constant of the release of the asymmetrical peak detector is 20 ms.
At very low frequencies, you can see that the differences between the minimum and maximum outputs from the detectors is largest. This is because, as we saw in Figure 6.58, the outputs of all of the detectors (excepting the peak detector with the long release time) is nearly the same as the absolute value of the input signal. As the signal goes up and down, so does the output of the detector. This appears in the graphs in Figures 6.64 and 6.65 as large differences in the maximum and minimum output levels.
As the frequency of the input signal goes up, the difference between the maximum and minimum levels of the outputs of the detectors decreases. In the case of the peak detector with the long release time, the two values converge on a level very near the peak level of the input signal. The pseudo-RMS and the symmetrical peak detector both converge on levels around 3 dB below the peak level of the signal. The odd one is the RMS detector. As you can see, at 500 Hz, the minimum and maximum levels of the output of the RMS detector are the same - at -3.01 dB relative to the peak level of the input. This means that there is no ripple in the output of the RMS detector at this particular frequency (where the period of the input signal is exactly two times the RMS time window). As we go slightly above 500 Hz, the maximum output of the RMS detector’s output increases and the minimum level decreases – in other words, the ripple in its output re-appears. At 1 kHz (when the period of the input signal is the same as the RMS time window) there is no ripple again... This behaviour repeats as we go up in frequency.
Why does the output of the RMS detector have no ripple at some frequencies and ripple at others? Let’s look at two signals as they sit in the RMS detector’s time window. Figure6.66 shows a signal with a period of exactly one RMS time window. The signal is the black sine wave. Four RMS time windows are shown, each at a different time (the 4 blue boxes). For each RMS time window, its RMS value is shown as a horizontal red line. There are two things to notice here. Firstly, the sine wave fits exactly in the boxes, therefore, each box has identical contents. This would be true regardless of where in the sine wave you are. Secondly, notice that the red lines all have the same value – this is because the output of the RMS window is stable, so there is no ripple in its output at this frequency.
Now compare this to the plot in Figure 6.67 which is the same as Figure 6.66, but with a slightly higher frequency. The length of the RMS time window is the same in both plots. Now you can see that the contents of the four different RMS time windows at different times in the sine wave are not the same, therefore their outputs are also different. This accounts for the ripple in the RMS detector output at this frequency.
Figures 6.64 and 6.65 show the results of a specific group of detectors with specific frequencies. This is useful for getting an intuitive understanding of the behaviours of the different detectors, but it’s not very useful if you have a detector with a different time constant or time window. Figures 6.68 and 6.69 show the same information in a more generalised form. In these, instead of the frequency on the x-axis, the ratio of the signal’s period to the RMS time window and the RC time constants. If these are confusing, just look at Figures 6.64 and 6.65 instead.
To now, we’ve been looking at the maximum and minimum output levels from the different detectors, however, these can be simplified into a single value stating the peak-to-peak ripple of the output of each detector. This is simply the vertical distance between the two plots for each detector in, for example, Figure 6.69. This version of displaying the same information is shown in Figures 6.70, 6.71, 6.72, and 6.73.
Another way to look at the behaviour of these level detectors is to consider the error
of the measurement that they provide. This is simply the difference between the value
given by the output of the detector and the value that we know is actually the right
answer. In this case, we know that we sent in a sine wave with a peak amplitude of 1 (and
therefore an RMS of 1∕ ) at all frequencies. So, these are the values we expect to see
coming out of the level detectors (1 for the peak detectors, 1∕
) at all frequencies. So, these are the values we expect to see
coming out of the level detectors (1 for the peak detectors, 1∕ for the RMS
detectors).
for the RMS
detectors).
As we already know, the outputs of all of the detectors are not constant over time, so we cannot really evaluate the real error. All we can do is look, as it bobs up and down, how close it is to the correct answer. These is shown in Figures 6.74 to 6.81.
Be wary of these plots, however... Although it looks like the peak detector with the separate attack and release times is the most accurate of the detectors shown here, this is only true after it has settled. As you can see, way back in Figure 6.60 this detector has the longest response time of the four detectors analysed here, so it takes more time to be right. Then again, you could argue that the other detectors are earlier, just more inaccurate... Would you rather have the right answer too late, or the wrong answer now? The choice is up to you...
Take a look back to the simplified block diagram of a compressor shown in Figure 6.49. Notice that the input gets split in two directions right away, going to the two different paths.
At the heart of the audio path is a device we have’t seen before – it’s drawn in block diagrams (and sometimes in schematics) as a triangle (so we know right away it’s an amplifier of some kind) attached to a box with an “X” through it on the left. This device is called a voltage controlled amplifier or VCA. It has one audio input on the left, one audio output on the right and a control voltage (or CV) input on the top. The amplifier has a gain which is determined by the level of the control voltage. This gain is typically applied to the current through the VCA, not the voltage – this is a new concept as well... but we’ll get to that later.
If you go to the VCA store and buy a VCA, you’ll find out that it has an interesting characteristic. Usually, it will have a logarithmic change in gain for a linear change in voltage at the control voltage input. For example, one particular VCA from THAT corporation has a gain of 0 dB (so input = output) if the CV is at 0 V. If you increase the CV by 6 mV, then the gain of the VCA goes down by 1 dB.
So, for that particular VCA, we could make Table 6.3 which we’ll use later.
| Control Voltage (mV) | Gain of Audio signal (dB) |
| -12 | +2 |
| -6 | +1 |
| 0 | 0 |
| +6 | -1 |
| +12 | -2 |
The only problem with the schematic so far is that the VCA is a current amplifier not a voltage amplifer. Since we prefer to think in terms of voltage most of the time, we’ll need to convert the voltage signal that we’re feeding into the compressor into a current signal of the same shape. This is done by sticking the VCA in the middle of an inverting amplifier circuit as shown in Figure 6.82:
Here’s an explanation of why we have to build the circuit like this. Remember back to the first stuff on op amps – one of the results of the feedback loop is that the voltage level at the negative input leg MUST be the same as the positive input leg. If this wasn’t the case, then the huge gain of the op amp would result in a clipped output. So, we call the voltage level at the negative input “virtual ground” because it has the same voltage level as ground, but there’s really no direct connection to ground. If we assume that the VCA has an impedance through it of 0Ω (a pretty safe assumption), then the voltage level at the signal input of the VCA is also the same as ground. Therefore the current through the resistor on the left in the above schematic is equal to the “Audio in” voltage divided by the resistor value. Now, if we assume that the VCA has a gain of 0 dB, then the current coming out of it equals the current going into it. We also happen to remember that the input impedance of the op amp is infinite, therefore all the current on the wire coming out of the VCA must go through the resistor in the feedback loop of the op amp. This results in a voltage drop across it equal to the current multiplied by the resistance.
Let’s use an example. If the “Audio in” is 1 Vrms, then the current through the input resistor on the left is 0.1 mArms. That current goes through the VCA (which we’ll assume for now has a gain of 0 dB) and continues on through the feedback resistor. Since the current is 0.1 mA rms and the resistor is 10 kΩ, then the voltage drop across it is 1 V rms. Therefore, the “Audio out” is 1 V rms but opposite in polarity to the input. This is exactly the same as if the VCA was not there.
Now take a case where the VCA has a gain of +6 dB for some reason. The voltage level at its input is 0 V (virtual ground) so the current through the input resistor is still 0.1 mA rms (for a 1 V rms input signal). That current gets multiplied by 2 in the VCA (because it has a gain of +6 dB) making it 0.2 mA rms. This all goes through the feedback resistor which results in a voltage drop of 10k * 0.2 mArms = 2 V rms (and opposite in polarity). Ah hah! The gain applied to the current by the VCA now shows up as a gain on the voltage at the output. Now all we need to do is to build the control circuitry and we have a compressor...
The control circuitry needs a number of things: a level detector, compression ratio adjustment, threshold, threshold level adjustment and some other stuff that we’ll get to. We’ll take them one at a time. For now, let’s assume that we have a compressor which is only looking at the RMS level to determine its compression characteristics.
This is an easy one. You buy a chip called an RMS detector. There’s more stuff to do once you buy that chip to make it happy, but you can just follow the manufacturer’s specifications on that one. This chip will give you a DC voltage output which is determined by the logarithmic level of an AC input. For example, using a THAT Corp. chip again... The audio input of the chip is measured relative to 0.316 V rms (which happens to be -10 dBV). If the RMS level of the audio input of the chip is 0.316 V rms, then the output of the chip is 0 V DC. If you increase the level of the input signal by 1 dB, the output level goes up by 6 mV. Conversely, if the input level goes down by 1 dB, then the output goes down by 6 mV. An important thing to notice here is that a logarithmic change in the input level results in a linear change in the output voltage. So, we build another table for future reference again:
| Input level (dBV) | Output Voltage (mV) |
| -8 | +12 |
| -9 | +6 |
| -10 | 0 |
| -11 | -6 |
| -12 | -12 |
Now, what would happen if we took the output from this RMS detector and connected it directly to the control voltage input of the VCA like in the diagram in Figure 6.83?
Well, if the input level to the whole circuit was -10 dBV, then the RMS detector would output a 0 V control voltage to the CV input of the VCA. This would cause it to have a gain of 0 dB and its output would be -10 dBV. BUT, if the input was -11 dBV, then the RMS detector output would be -6 mV making the VCA gain go up by 1 dB, raising the output level to -10 dBV. If the input level was -9 dBV, then the RMS detector’s output goes to 6 mV and the VCA gain goes to -1 dB, so the output is -10 dBV. Essentially, no matter what the input level was, the output level would always be the same. That’s a compression ratio of ∞ : 1.
Although the circuit above would indeed compress with a ratio of ∞ : 1, that’s not terribly useful to us for a number of reasons. Let’s talk about how to reduce the compression ratio. Take a look at the circuit in Figure 6.84.
If the potentiometer has a linear scale, and the wiper is half-way up the pot, then the voltage at the wiper is one half the voltage applied to the top of the pot. This means, in turn, that the voltage applied to the CV input of the VCA is one half the voltage output from the RMS detector. How does this effect us? Well, if the input level of the circuit is -10 dBV, then the RMS detector outputs 0 V, the wiper on the pot is at 0 V and the gain of the VCA is 0 dB, therefore the output level is -10 dBV. If, however, the input level goes up by 1 dB (to -9 dBV), then the RMS detector output goes up by 6 mV, the wiper on the pot goes up by 3 mV, therefore the gain of the VCA goes down by 0.5 dB and the output level is -9.5 dB. So, for a 2 dB change in level at the input, we get a 1 dB change in level at the output – in other words, a 2:1 compression ratio.
If we put the pot at another location, we change the ratio of the voltage at the top of the pot (which is dependent on the input level to the RMS detector) to the gain (which is controlled by the wiper voltage). So, we have a variable compression ratio from 1:1 (no compression) to infinity:1 (complete limiting) and a rotation point at -10 dBV. This is moderately useful, but real compressors have a threshold. So – how do we make this happen?
The first thing we’ll need to make a threshold detection circuit is a way of looking at the signal and dividing it into a low voltage area (in which nothing gets out of the circuit) and a high area (in which the output = the input to the circuit). We already looked at how to do this in a rather crude fashion – it’s called a half-wave rectifier. Since the voltage of the wiper on the pot is going positive and negative as the input signal goes up and down respectively, all we need to do is rectify the signal after the wiper so that none of the negative voltage gets through to the CV input of the VCA. That way, when the signal is low, the gain of the VCA will be 0 dB, leaving the signal unaffected. When the signal goes positive, the rectifier lets the signal through, the gain of the VCA goes down and the compressor compresses.
One way to do this would simply be to put a diode in the circuit pointing away from the wiper. This wouldn’t work very well because the diode would need the 0.7 V difference across it to turn on in the first place. Also, the turn-on voltage of the diode is a little sloppy, so we wouldn’t know exactly what the threshold was (but we’ll come back to this later). what we need then, is something called a precision rectifier – a circuit that looks like a perfect diode. This is pretty easy to build with a couple of diodes and an op amp as is shown in the circuit in Figure 6.85.
Notice that the circuit has two effects – the first is that it is a half-wave rectifier, so only the positive half of the input gets through. The second is that it is an inverting amplifier, so the output is opposite in polarity to the input – therefore, in order to get things back in the right polarity, we’ll have to flip the polarity once again with a second inverting amplifier with unity gain.
If we add this circuit between the wiper and the VCA CV input like the diagram shown in Figure 6.86, what will happen?
Now, if the input level is -10 dBV or lower, the output of the RMS detector is 0 V or lower. This will result in the output of the half-wave rectifier being 0 V. This will be multiplied by -1 in the polarity inversion, resulting in a level of 0 V at the CV input of the VCA. This means that if the input signal is -10 dBV or lower, there is no gain change. If, however, the input level goes above -10 dBV, then the output of the RMS detector goes up. This gets through the rectifier and comes out multiplied by -1, so for every increase in 1 dB above -10 dBV at the input, the output of the rectifier goes DOWN by an amount determined by the position of the wiper. This is multiplied by -1 again at the polarity inversion and sent to the CV input of the VCA causing a gain change. So, we have a threshold at -10 dBV at the input. But, what if we wanted to change the threshold level?
In order to change the threshold level, we have to trick the threshold detection circuit into thinking that the signal has reached the threshold before it really has. Remember that the output of the RMS detection circuit (and therefore the wiper on the pot) is DC (well, technically speaking, it varies if the input signal’s RMS level varies, but we’ll say it’s DC for now). So, we need to mix some DC with this level to give the input to the rectification circuit an additional boost. For example, up until now, the threshold is -10 dBV at the input because that’s where the output of the RMS detector crosses from negative to positive voltage. If we wanted to make the threshold -20 dBV, then we’d need to find out the output of the RMS detector if the signal was -20 dBV (that would be -60 mV because it’s 6 mV per dB and 10 dB below -10 dBV) and add that much DC voltage to the signal before sending it into the rectification stage. There are a couple of ways to do this, but one efficient way is to combine an inverting mixer circuit with the half-wave rectifier that’s already there.
The threshold level adjustment is just a controllable DC level which is mixed with the DC level coming out of the RMS detector. One important thing to note is that when you turn UP this level to the top of the pot, you are actually getting a lower voltage (notice that the top of the pot is connected to a negative voltage supply). Why is this? Well, if the output of the threshold level adjustment wiper is 0 V, this gets added to the RMS detector output and the threshold stays at -10 dBV. If the output of the threshold level adjustment wiper goes positive, then the output of the RMS detector is increased and the rectifier opens up at a lower level, so by turning UP the voltage level of the threshold adjustment pot, you turn DOWN the threshold. Of course, the size of the change we’re talking about on the threshold level adjustment is on the order of mV to match the level coming out of the RMS detector, so you might want to be sure to make the maximum and minimum values possible from the pot pretty small. See the THAT Corp .pdf file linked at the bottom of the page for more details on how to do this.
So, now we have a compressor with a controllable compression ratio and a threshold with a controllable level. All we need to do is to add an output gain knob. This is pretty easy since all we’re going to do is add a static gain value for the VCA. This can be done in a number of ways, but we’ll just add another DC voltage to the control voltage after the threshold. That way, no matter what comes out of the threshold, we can alter the level.
The diagram in Figure 6.88 shows the whole circuit. Note that the output gain control has the + DC voltage at the top of the pot. This is because it will become negative after going through the polarity inversion stage, making the VCA go up in gain. Since this DC voltage level is added to the control voltage signal after the threshold detection circuit, it’s always on – therefore it’s basically the same as an output level knob. In fact, it is an output level knob.
Everything I’ve said here is basically a lead-up to the pdf file below from THAT Corp. It’s a good introduction to how a simple RMS-based compressor works. It includes all the response graphs that I left out here, and goes a little further to explain how to include a soft knee for your circuit. Definitely recommended reading if you’re planning on learning more about these things...
Basic Compressor/Limiter Design – from THAT Corporation www.thatcorp.com/datashts/an100a.pdf
Users Manual for the GML 8900 Dynamic Range Controller www.gmlinc.com/8900.pdf
Once upon a time when you were a kid, you probably did a science experiment where you made a compass using a tray of water and a sewing needle. The only work involved in the experiment was to turn the needle into a magnet by stroking it over and over with a permanent magnet. The lesson here is that if you put a piece of iron in a magnetic field, you can turn it into a magnet.
Let’s make soup! Unfortunately, not a good French onion soup, or a seafood chowder, however... We’ll make a slurry of little needles (usually called a magnetic oxide because it’s made out of things like ferric oxide, for example) suspended in a non-magnetic liquid binder. We’ll then pour this goo on a wide sheet of polyester and let it dry so that the little needles are stuck to the sheet. Just before we dry it, we run the polyester with the goo on it through a really strong magnetic field so all the needles are pointing in the same direction – just like little compasses. Eventually, we’re going to roll up this sheet, so we’ll put a carbon coating on the back of it so that it’s slippery and it doesn’t build up static electricity. Then we take the wide sheet and slice it into strips ranging from 0.125 to 2 inches wide.
A cross section of this stuff looks like Figure 6.89
The important thing about the magnetic oxide coating on the polyester is that it is pretty easy to magnetize. If we put it in a strong magnetic field and then take it out, it will maintain that field in the coating, just like the needle that we magnetized to make a compass back when we were kids.
So, how do we magnetize the coating? We already know two useful things from Section 2.6: the first is that if we run current through a wire, we get a magnetic field around it. The second is that, if that wire is coiled around an iron bar, the iron bar will act like a magnet. So, let’s take an iron bar and bend it so that the two ends almost touch each other. We’ll also coil a wire around it so that the whole thing looks like Figure 6.90. This is a very basic model of a record head of an analog tape recorder. (Actually, it also works as a playback head.)
When we put current in the coil, the iron bar it’s coiled around temporarily becomes a magnet. This, in turn, causes magnetic lines of force to go from one end of the bar to the other across the narrow gap that we created (seen at the top in Figure 6.90. If we look at a close-up of those magnetic lines of force, we’d see something like Figure 6.91.
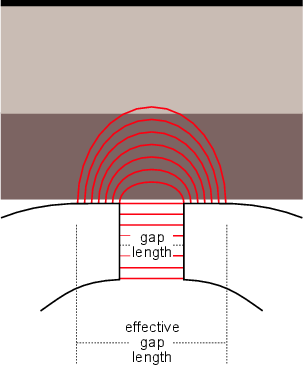
In its most simple form, if we send an audio signal into the coil of wire wrapped around the tape head, we’ll cause the magnetic field to change in strength and polarity at the gap of the record head. If we leave the magnetic tape sitting on the head while this happens, we’ll be causing that magnetic field to be stored on the tape. If we want to keep the magnetic field stored on the tape, then we’ll move it away from the head before the next signal comes in. So, we move the tape continuously across the head while the magnetic field changes (caused by changes in the current in the coil which, in turn are caused by changes in the audio signal). As the tape moves away from the gap (from left to right in Figure 6.91, the magnetic field that was imposed on it by the gap of the record head is maintained and we have a recording of our signal. Then all we have to do is to figure out how to play it back.
This is where things get really easy. Remember that our tape is now basically a permanent magnet. If we put it next to an iron bar, then the iron bar conducts the magnetic lines of force. If the iron bar has a coil wrapped around it, and the magnetic lines of force going through the bar change, then we induce a current in the coil that is proportional to the change in the strength of the magnetic field. Therefore, if we continuously move the tape across the head gap, we continuously change the magnetic field and therefore generate a current in the coil that is proportional to the magnetic field on the tape, which, as you probably remember is proportional to the original audio signal. Consequently, we get a signal out of the coil that is representative of our original signal.
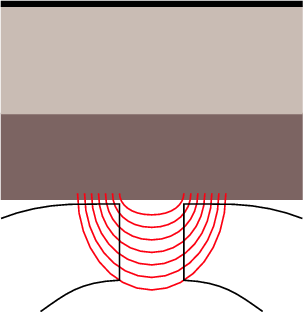
Okay, so I oversimplified a little bit, but the basic idea is fundamentally correct. However, let’s look a little deeper into the process and talk about some of the terms that you might need to know. These definitions are all taken from [Woram, 1989].
As we’ve already seen, if we apply a current to the coil that’s wrapped around the head, we generate a magnetic field around the gap in the head. That magnetic field around the record head is called the recording field. It’s measured in amperes per meter (A/m) and it’s abbreviated H.
If you put a piece of magnetic tape in a recording field, and then remove it, some magnetic field will remain on the tape. The strength of that magnetic field is called the remanent tape magnetization. It’s measured in amperes per meter (A/m) and it’s abbreviated Mr.
We’ve already seen terms like voltage and current to describe the quantities associated with electricity, however, we need to look at how magnetism is quantified. Magnetic lines of force are also known as magnetic flux. The strength of magnetic flux is measured in webers (abbreviated Wb) named after Wilhelm E. Weber. Older textbooks will use the maxwell (or Mx) instead, named after James Clerk Maxwell. If you have to convert from one to the other, 1 Wb = 108 Mx [Woram, 1989].
If you have a permanent magnet, you can measure not only its strength, but how strong it is for a given surface area. For example, you can have two magnets one big and one small, both able to lift a block of iron that weighs exactly 1 kg. Both magnets have the same strength, but the small one has a higher density of magnetic flux, because it has the same total flux distributed over a smaller area.
This is also true of the magnetism stored on a piece of analog tape (which can also be considered to be a permanent magnet). Since there is a magnetic signal stored on the coating of the tape, we can think of it as a permanent magnet that has a different flux in different locations (if it didn’t, the signal wouldn’t change in time and we would just have a DC component).
So, the magnetic flux density on the tape is a measure of the magnetic flux (in Wb) per area of tape (in m2). Therefore magnetic flux density is measured in Wb/m2
Let’s put a piece of magnetic tape next to a recording head. We’ll apply a signal to the recording head and generate a known flux density around the head which in turn is applied to the tape. That causes the magnetic tape to become magnetized. If we turn off the signal at the record head, there will be some amount of magnetic strength left in the tape, but not as much as the amount that we applied to the tape. However, the magnetic strength of the tape won’t drop to zero just because we turned off the magnetic field around the record head, either. The amount of magnetic strength left in the tape will be something between the flux density that we applied, and zero. The amount of magnetic flux density that is left on the tape after the external magnetic force (applied by the record head) has been turned off is called the tape’s retentivity.
Since retentivity is a measure of magnetic flux density that remains in the tape after we’ve turned off an external magnetic field, it’s measured in Wb/m2.
The tape retentivity is not zero, otherwise it wouldn’t work. If we turn off the external magnetic field, there is some magnetic field left on the tape. What if we wanted to get the magnetic field on the tape back to zero? We’d have to apply an external magnetic field with a reverse polarity to “undo” the magnetic field on the tape. The strength of the reversed polarity field that’s required to get the magnetic field on the tape back to zero is called the tape’s coercivity. It’s abbreviated H and measured in amperes per meter (A/m) (because it’s a magnetic field strength, not a flux density).
Back at the beginning of Section 2.8, I made a very short, passing reference to the fact that an iron bar is a great conductor for magnetic lines of force. Of course, iron can also conduct electrical current, but that’s a completely different issue right now. If you have a magnet, there will be lines of magnetic force around it. If you put an iron bar near (but not attached to) the magnet, the lines of force will find it easier to go through the iron than the air, so they’ll concentrate into the iron.
This is the intuitive way of thinking of things. The more technical way is to measure the magnetic flux density, B, inside the iron bar, then measure the magnetic field strength, H, that’s applied by an external magnet. The ratio of these two is called the permeability of the iron. It’s the magnetic equivalent of resistance. The higher the permeability, the easier it is for the magnetic lines of force to “travel” through the substance. The symbol for permeability if μ and it’s measured in henries per meter (H/m).
You’re may already be familiar with electrical operating levels in analog recording and playback equipment. If so, then you know that, on a professional piece of equipment, when your output level VU meter says “0 dB,” then you should be getting +4 dBu at the output. (If this is completely unfamiliar to you, don’t worry. It’ll be thoroughly discussed in Section 10.1.)
In the world of analog tape, we have a similar issue. The question is, “when the record meter on my deck reads 0 dB VU, how much am I magnetizing the tape?” The answer to this question is your operating level (also known as the reference level or the reference fluxivity). It’s a measure of the fluxivity on the tape, measured in Wb per meter.
How do you decide on what operating level to use? This depends on the type of tape that you’re using, and what kind of music you record.
Analog recording tape has some maximum amount of fluxivity that it can “store” – an amount called the maximum output level or MOL. Different types of tape have different MOL’s. This is defined as the point where the tape starts to saturate, and the difference in the signal you tried to put on the tape and the signal that comes back off the tape causes a distortion of 3% THD. (A definition of THD can be found in Section 7.2.16.) For example, Ampex 456 will produce 3% distortion when you try to put a sine wave with a level of approximately 762 nWb/m (nanoWebers per meter). By comparison, 3M 206 tape will produce the same 3% distortion is you try to put a sine wave with a level of 465 nWb/m.
So, if you’ve set your record head to put a given amount of magnetism on the tape and you record an increasingly high level of signal, you’ll distort the 3M tape before the Ampex tape. Therefore, you should set the standard operating level lower if you regularly use the 3M tape than if you use the Ampex tape.
Let’s also say that you record death metal with absolutely no dynamic range and I record classical music and I’ve never seen a compressor in my life, but we both use the same tape. You know exactly what your maximum level will be, but I never will, because my orchestra might hit a really loud point and surprise me. Therefore, I need more “headroom” when I record – more space to put extra level in case I need it. You don’t need this headroom because death metal never surprises. Consequently, you can set your operating level to a higher level than I can. This is because you always know how far away you are from saturating the tape and therefore distorting the signal – I almost never do...
Once upon a time, a typical operating level was 185 nWb/m. Back about 15 years ago, 250 nWb/m was a more standard operating level - 3 dB higher than the older level. Once analog tapes with extremely high operating levels were introduced on the marker (such as Ampex 499 tape) people could push their operating level even higher. These numbers are not standard for all recording studios, however, so you will have to know the operating level before you start recording. For example, if you are used to working with a deck that is aligned to 185 nWb/m and you do a gig in a studio that’s aligned at 250 nWb/m, you’ll distort your tape 3 dB earlier than you’re used to because the deck is putting more magnetism on the tape for the same reading on the meters.
The moral of this story is to know the behaviour of your tape and your operating level.
Let’s look a little more carefully about the behaviour of analog recording tape when we try to put a signal on it. If tape were perfect, it would have a linear transfer function like the one shown in Figure 6.93. In this case, the signal that we get off the tape is identical to the signal we try to put on it. This is a lovely idea. Unfortunately, it is very far from the way tape actually behaves as we’ll see...
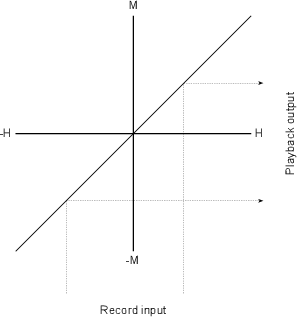
Let’s start with a piece of analog tape that has no magnetic signal on it. Therefore M = 0. We’ll start with the tape in a place that has no magnetic field, and we’ll slowly apply a magnetic field with a positive polarity (indicating that it’s pointing in a given direction – we don’t know that direction, but we do know that a negative field would be in the opposite direction) to it from an external source like a permanent magnet. Figure 6.94 shows how the tape magnetization will behave if we do this. If we apply a small magnetic field, a smaller field will be stored on the tape. As we apply more and more external magnetic field, more and more strength will be stored on the tape. Eventually, you’ll notice that there is a nearly-linear relationship between the applied field and the stored field. If we increase the magnetic field even more, we’ll start getting closer to the maximum magnetism that can be stored on the tape – the point of saturation, so the curve gets more and more horizontal. No matter how much further we try to push the tape, we can never get a bigger magnetic field from the tape.
Now we have a tape that has been magnetized to its saturation point. What happens if we try to de-magnetize it. One way to do this is to put it in a weak magnetic field with the same polarity. The applied field, H will cause the tape to have a magnetism more like the applied field than the one it had. However, the tape doesn’t automatically have the same magnetism as the applied field. In fact, it will maintain some amount of magnetism as can be seen in Figure 6.95. As we apply a weaker and weaker field, we will pull the tape back to less and less of a magnetic signal. Eventually, we’ll get to H = 0 – in other words, no magnetic field is applied to the tape. However, some magnetism is left on the tape. The amount of the remaining field is the tape’s retentivity, as we have seen already in Section 6.3.2.
So, now the tape is in a space free of a magnetic field, but it’s still magnetized. If we now start applying a stronger and stronger external magnetic field, but with a polarity opposite to the one we applied before, we’ll be bringing the magnetism on the tape closer and closer to 0 – essentially undoing everything we did. This behaviour is shown in Figure 6.96. You’ll also note that, if the strength of the external field is increased more and more, we’ll eventually reach the saturation of the tape, but in the opposite polarity.
If we reduce the strength of the external field, we’ll start reducing the magnetic field on the tape just as we did in the positive direction. This is shown in Figures 6.96 and 6.97. The final curve that results is called a hysteresis loop. The word comes from the Greek word hystérsis meaning “a state of delay”[Woram, 1989].
So far, the description of the behaviour of the tape has assumed that we apply a magnetic field to the tape, and then apply a different magnetic field (for example, as if we were going to try to erase it). However, it’s usually more useful to apply a magnetic field, and then leave the tape alone. That way, the signal that we applied remains on the tape. In this case, the curve to describe the behaviour of the tape has already been shown (or at least half of it was...) in Figure 6.94. If we assume that the tape behaves the same in the opposite polarity (and it does...) then the complete curve will look like Figure 6.98.
One important thing to notice about this curve is that there are two nearly-linear parts on it. This is an important piece of information for the next section.
We started in Section 6.3.3 by wishing that analog tape had a perfectly linear transfer function, but we found out that it doesn’t. However, we did see in Figure 6.98 that there are linear components on the tape’s M-H curve. These can be used to our advantage as is shown in Figure 6.99.
Let’s take our audio signal and ensure that its peak-peak amplitude is about the same as the size of one of the two linear components on the tape’s M-H curve. We then apply a DC offset (usually called a DC bias) to the signal so that it sits on one of the linear portions of the curve.
This will actually work – we’ll get a linear representation of our signal stored on the analog tape and we’ll be able to read it back with a playback head. The only problem is that we’re not using the full potential of the tape, so we get a very poor signal to noise ratio.
Go to the kitchen and get a bag of flour. Open it up and try to pour some out. You’ll tip the bag higher and higher and nothing will happen. Then, suddenly, a big clump of flour will suddenly drop out of the bag and make a huge mess. This is a bad way to pour flour out of a bag.
A better way is to hold the bag of flour, and start shaking it gently back and forth sideways to get the flour particles moving against each other. Then, while you’re shaking, tip the bag and start pouring. The flour will come out smoothly if you keep shaking.
Magnetic tape behaves in a similar way. Take a look at the M -H curve in Figure 6.98. It shows that if you apply a weak magnetic field to the tape and take it away, nothing will be printed on the tape (just like the fact that no flour will come out of the bag...) If you apply a bigger magnetic field and take it away, you’ll leave a magnetic field on the tape (big clump of flour...). So, what’s the analog magnetic tape equivalent of shaking the bag of flour? What we’ll do is make a really high frequency, really high amplitude sine wave – something on the order of 150 kHz – 400 kHz. We’ll then use our audio signal (which is a comparatively low frequency) and add it to the sine wave. The result of this is shown in Figure 6.100. The high frequency tone is called AC bias and has been used in all analog tape recorders since about the 1940’s.
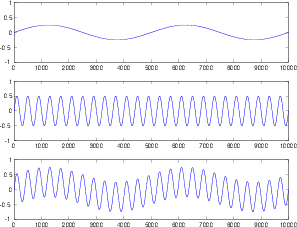
How and why does this work? Apparently, no one is really sure, but there are some theories. The best one I’ve heard is that the AC bias signal basically shakes things up a lot, applying a random behaviour to the little magnetic needles with an amplitude up around the area where the tape saturates. As the tape moves away from the record head, the needles move out of that randomizing tone and what’s left as it does away is the offset of the bias – which is our original signal that we’re trying to record.
NB: Special thanks to Peter Cook for the flour analogy.
Back in Section 6.3.1 I oversimplified a bit and said that the magnetic signal on the tape produces a field that temporarily magnetizes the playback head. If the magnetic field changes (by moving the tape, for example) then the magnetic field around the coil around the head changes and we get a current output. This is essentially true, but we have to look at things in a little more detail.
The magnetic field that is “read” by the playback head is a measurement of the difference in magnetic field across the head gap length. Take a look at Figure 6.101. If you have a very low frequency, and therefore a very long wavelength on the tape, there is very little difference in magnetic field across the gap (because the gap length is small compared to the wavelength). Another way to think of this is that there is very little phase difference across the gap length. Consequently, there is a very small magnetic field generated in the head, and we don’t get much output. The lower the frequency, the longer the wavelength and the smaller the output.
As the frequency is increased, the difference in the signal across the gap length increases (it becomes more and more different) so we get more output from the playback head. In fact, we get 6 dB more output for every increase in frequency of 1 octave.
Eventually, we get to a point where the wavelength is two times the gap length. This is where we have the maximum possible output from the head, because we have the maximum possible difference in magnetic field across the gap length.
What happens when the frequency goes higher than this? Now, we have more than half a wavelength across the gap, and the output starts to drop again. This will continue to drop until we reach a point where the wavelength is equal to the gap length and we get no output because the difference in magnetic field across the gap is nothing.
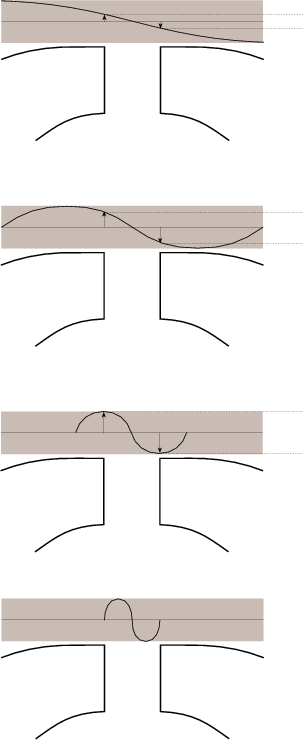
So what? Well, we know a couple of things:
Therefore we can conclude a couple of things:
So, we can conclude that we should run the tape at a high speed – the higher the better. This is true, however there is one minor problem. The higher the tape speed, the more tape you use and the more money you spend. So, if you want a better signal from your tape, you have to spend more money. Sorry.
Just to give you an idea of typical gap lengths, a playback head will have a gap length between 1.5 and 6 μm whereas a record head doesn’t need to be as small – typically between 2.5 and 12 μm[Woram, 1989].
In order to ensure that your tape recorder is behaving properly, you have to clean, demagnetize and calibrate it. Cleaning the heads is an event that should happen frequently – a good practice is to clean the heads before every session to get dirt and magnetic goo from the previous session’s tape off the head – you don’t want anything between the record head and the tape you’re recording on. Most people do this with cotton swabs and head cleaner. You could use alcohol, but this may have a tendency to dry out the rubber components like the pinch roller on the tape deck. It’s also a good idea to be careful to not get the cleaning fluid all over the place around the head block (the big assembly that holds the erase, record and playback heads). This is because the cleaning fluid is also a degreaser, and you do not want to dissolve the grease inside the bearings in your capstan and pinch roller.
Over time, the playback and record heads may become permanent magnets. This is a bad thing because it’s the equivalent of applying a DC offset to your signal. To reduce this problem, you can demagnetize your heads using a demagnetizer. This is basically an electromagnet that oscillates with a very high-strength magnetic field, going positive and negative. You should switch on the demagnetizer when it’s far away from the heads, bring it in close to the heads, being very careful to not touch the heads with the demagnetizer, then move it far away again before switching it off. Always remember that the demagnetizer is also a very good bulk tape eraser, so don’t do this while there’s tape in the area... You’ll wish you hadn’t if you do.
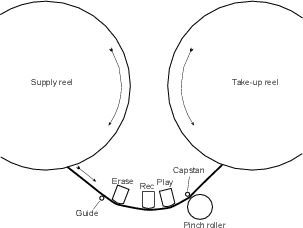
In order to calibrate your tape deck, you’ll need to spend a little money first. You’ll have to buy a calibration tape. This will not be cheap, but it will be worth the cost. A calibration tape is just a small reel of analog tape that has a bunch of test tones recorded on it. The thing that makes it special is that the test tones are absolutely guaranteed to be at a known level and recorded with proper alignment. This gives you a reference that you can use to calibrate your own tape deck. This is similar to owning an oscilloscope so that you know the voltage level of an output – a calibration tape lets you reference your recorder to some standard external device.
At the risk of sounding like an advertisement, most people buy their calibration tapes from a company called Magnetic Reference Laboratories. They also have a good paper on their website that tells you how to calibrate your tape recording using a calibration tape. You can get that paper and order their tapes online at www.mrltapes.com.
WRITE THIS SECTION
Azimuth
Rotation
Zenith
Rotation
Fringing
Using AC bias for recording changes pretty much all characteristics of the tape’s behaviour. Consequently, the level and frequency of the AC bias must be calibrated to customize the performance of your tape on your tape recorder. Take a look at Figure 6.108 which shows the type of information you’ll get with your tape when you buy a reel of it.
Noise in audio can very basically and generally be defined as anything in the audio signal that we don’t want to be there. Technically speaking, “noise” is random, so a periodic signal (such as as an unwanted hum in the system) cannot be considered noise. However, we’ll ignore that strict definition for the purposes of this chapter and throw everything that is not your signal under the general heading of noise.
There are two basic sources of noise in an audio chain, internal noise and noise from external sources.
Internal noise is inherent in the equipment, and can never be eliminated completely. If you have something as simple as a resistor, then the molecules bumping around inside it due to heat make some noise called thermal noise. The only thing you can hope to do is to reduce the noise level relative to the signal strength. You can either mask (or hide) the noise with better gain structures2 or just go out and buy better equipment...
Noise from external sources is caused by Electromagnetic Interference, also known as EMI. Three simultaneous things must exist in order for this to be a problem. You’ll need:
If you take away any of these three, then EMI ceases to be a problem. For example, if you have a noise source and a receiver, but no transmission medium between them, then there’s no problem because the noise has no way of reaching the receiver. Typically, you’ll always have a receiver, since this is usually the equipment you’re using to do the recording, however, you might be able to eliminate either the noise source or the transmission medium if you’re having a problem. As a very simple example, if you’re recording a guitar amp (a receiver) that is humming because the studio lights are dimmed (the noise source), then you can just turn off the lights (in other words, remove the noise source) to solve the problem.
EMI has four possible means of transmission:
Each of these are discussed individually below.
Common impedance coupling occurs when there is a shared wire between the source and the receiver.
As we’ve seen many times so far, in almost every piece of audio gear, the signal is represented by a change in voltage over time. That voltage is referenced to a constant voltage level that we call “ground,” so what we’re really looking at is a difference between two voltages. We usually assume that our ground voltage is 0 V relative to the world (This is why we call it “ground” – we assume that there is no difference between the local ground voltage and the voltage level of the actual ground under your feet. This is also why, in some countries, you call it “earth” instead of “ground”.) which makes it easy to find the difference between our two voltages. However, there are some cases where this is not true.
Let’s think about an analogy for a paragraph before we move on. When someone asks you how tall you are, you usually give them an answer that is a measurement from your feet to the top of your head. If you’re standing on the ground, or on the top of a building, you will still be the same height. This is because you’re assuming that your feet start at 0 m. So, if you have two people of the same height stand next to each other, then they can look each other in the eye. However, if one of the two is standing on a box, then there will appear to be a difference in height even though there isn’t. Both people are still the same height, however, the starting point of 0 m is different for the two. The same is also apparent if one of the people is standing on a wharf, and the other is standing on a boat tied to the same wharf. As the boat bobs up and down with the waves in the water, the difference in the apparent height of the two people changes. If you couldn’t see the boat, and you were really dumb, then you might actually be convinced that the difference in their heights actually was changing.
This can also happen in differences in voltage between two pieces of audio gear. If you think of the two people as two pieces of audio gear, and their heights as the voltage levels of the two audio signals, then the concept of differences in ground potential becomes important.
START WORKING HERE AND FIX THE FOLLOWING PARAGRAPH
Let’s say, for example, that two units, a microphone preamplifier and a food processor, are both connected to the same power bar. This means that, from the power bar to the earth, the two devices are making use of the same wires for their references to ground. This means that, in the case of this shared ground wire, they are coupled by a common impedance to the earth (the impedance of the ground wire from the power bar to the earth). If one of the two devices (the food processor maybe...) is a source of noise in the form of alternating current, and therefore voltage (because the wire has some impedance and V=IR) at the ground connection in the powerbar, then the “ground” voltage at the microphone preamp will modulate. If this is supposed to be a DC 0 V forever relative to the rest of the studio, and it isn’t, then the mic pre will output the audio signal plus the noise coupled from the common impedance.
Electrical field coupling is determined by the capacitance between the source and the receiver or their transmission media.
Once upon a time, we looked at the construction of a capacitor as being two metal plates side by side but not touching each other. If we push electrons into one of the plates, we’ll repel electrons out of the other plate and we appear to have “current” flowing through the capacitor. The higher the rate of change of the current flowing in and out of the plate, the easier it is to move current in and out of the other plate.
Consider that if we take any two pieces of metal and place them side by side without touching, we’re going to create a capacitor. This is true of two wires side by side inside a mic cable, or two wires resting next to each other on the floor or so on. If we send a high frequency through one of the wires, and we have some small capacitance between that wire and the “receiver” wire, we’ll get some signal appearing on the latter.
The level of this noise is proportional to:
The level of the noise is inversely proportional to
Magnetic field coupling is determined by the mutual inductance between the source and receiver.
Remember back to the chapter where we talked about the right hand rule and how, when we send AC through a wire, we generate a pulsing magnetic field around it whose direction is dependent on the direction of the current and whose amplitude (or distance from the wire) is proportional to the level of the current. If we place another wire in this moving magnetic field, we will induce a current in the second wire – which is how a transformer works.
Although this concept is great for transformers, it’s a problem when we have microphone cables sitting next to high-current AC cables. If there’s lots of current through the AC cable at 60 Hz, and we place the mic cable in the resulting generated magnetic field, then we will induce a current in the mic cable which is then amplified by the mic preamplifier to an audible level. This is bad, but there are a number of ways to avoid it as we’ll see.
The level of this noise is proportional to:
The level of this noise is inversely proportional to:
Electromagnetic radiation occurs when the source and receiver are at least 1/6th of a wavelength apart (therefore the receiver is in the far field – where the wavefront is a plane wave and the ratio of the electrostatic to the electromagnetic field strengths is constant)
An example of noise caused by electromagnetic radiation is RFI or Radio Frequency Interference caused by radio transmitters, CB etc.
www.engineeringharmonics.com
Grounding and Shielding for Sound and Video, Philip Giddings
How do we get rid of the noise caused by the four sources described in Chapter 6.4? There are three ways: shielding, balancing and grounding
This is the first line of defense against outside noise caused by high-frequency electrical field and magnetic field coupling as well as electromagnetic radiation. The theory is that the shielding wire, foil or conduit will prevent the bulk of the noise coming in from the outside.
It works by relying on two properties
1. Reflection back to the outside world where it can’t do any harm... (and, to a small extent, re-reflection within the shield, but this is a VERY small extent)
2. Absorption – where the energy is absorbed by the shield and sent to ground.
The effectiveness of the shield is dependent on its:
1. Thickness – the thinner the shield the less effective. This is particularly true of low-frequency noise... Aluminum foil shield works well at rejecting up to 90 dB at frequencies above 30 MHz, but it’s inadequate at fending off low-frequency magnetic fields (in fact it’s practically transparent below 1 kHz), We rely on balancing and differential amplifiers to get rid of these.
2. Conductivity – the shield must be able to sink all stray currents to the ground plane more easily than anything else.
3. Continuity – we cannot break the shield. It must be continuous around the signal paths, otherwise the noise will leak in like water into a hole in a boat. Don’t forget that the holes in your equipment for cooling, potentiometers and so on are breaks in the continuity. General guideline: keep the diameter of your holes at less than 1/20 of the wavelength of the highest frequency you’re worried about to ensure at least 20 dB of attenuation. Most high-frequency noise problems are caused by openings in the shield material.
It is commonly believed even at the highest levels of the audio world that a balanced signal and a differential or symmetrical signal are the same thing. This is not the case. A differential (or symmetrical) signal is one where one channel of audio is sent as two voltages on two wires. These two signals are identical in every respect with the exception that they are opposite in polarity. These signals are known by such names as “inverting and non-inverting” or “Live and Return” – the “L” and “R” in XLR (the X is for eXternal – the ground)3 . They are received by a differential amplifier which subtracts the return from the live and produces a single signal with a gain of 6.02 dB (since a signal minus its negative self is the same as 2 times the signal and therefore about 6 dB louder). The theoretical benefit of using this system is that any noise that is received on the transmission cables between the source and the receiver is (theoretically) identical on both wires. When these two versions of the noise arrive at the receiver’s differential amplifier, they are theoretically eliminated since we are subtracting the signal from a copy of itself. This is what is known as the Common Mode Rejection done by the differential input. The ability of the amplifier to reject the common signals (or mode) is measured as a ratio between the output and one input leg of the differential amplifier and is therefore called the Common Mode Rejection Ratio (CMRR).
Having said all that, I want to come back to the fact that I used the word “theoretical” a little too often in the last paragraph. The amount and quality of the noise on those two transmission lines (the live and the return) in the so-called balanced wire is dependent on a number of things.
The grounding of audio equipment is there for one primary purpose: to keep you alive. If something goes horribly wrong inside one of those devices and winds up connecting the 120 V AC from the wall to the box (chassis) itself, and you come along and touch the front panel while standing in a pool of water, YOU are the path to ground. This is bad. So, the manufacturers put a third pin on their AC cables which is connected to the chassis on the equipment end, and the third pin in the wall socket.
Let’s look at how the wiring inside a wall socket is connected to begin with. Take a look at Figures 6.109 to 6.113.


The third pin in the wall socket is called the ground bus and is connected to the electrical breaker box somewhere in the facility. All of the ground busses connect to a primary ground point somewhere in the building. This is the point at which the building makes contact with the earth through a spike or piling called the grounding electrode. The wires which connect these grounds together MUST be heavy-gauge (and therefore very low impedance) in order to ensure that they have a MUCH lower impedance than you when you and it are a parallel connection to ground. The lower this impedance, the less current will flow through you if something goes wrong.
MUCH MORE TO COME!
| Conductor Out From | Low Dynamic Range | Med DR | Med DR | High DR | High DR |
| (< 60 dB) | (60 to 80 dB) | (60 to 80 dB) | (> 80 dB) | (> 80 dB) | |
| Low EMI | High EMI | Low EMI | High EMI | ||
| Ground Electrode | 6 | 2 | 00 | 00 | 0000 |
| Master Bus | 10 | 8 | 6 | 4 | 0 |
| Local Bus | 14 | 12 | 12* | 12* | 10* |
| Max. Resist. for any cable | 0.5Ω | 0.1Ω | 0.01Ω | 0.001Ω | 0.0001Ω |
Grounding and Shielding for Sound and Video by Philip Giddings www.engineeringharmonics.com
Hum and Buzz in Unbalanced Interconnect Systems by Bill Whitlock www.jensen-transformers.com/an/an004.pdf
Sound System Interconnection www.rane.com/note110.html
Grounding www.trinitysoundcompany.com/grounding.html
Ground loop problems and how to get rid of them www.hut.fi/Misc/Electronics/docs/groundloop
Considerations in Grounding and Shielding Audio Devices www.rane.com/pdf/groundin.pdf
A Clean Audio Installation Guide – from Benchmark Media www.benchmarkmedia.com/appnotes-a/caig
Fundamentals of Studio Grounding, Richard Majestic: Broadcast Engineering, April 1992
The Proper Use of Grounding and Shielding, Philip Giddings: Sound and Video Contractor, September 20, 1995
A microphone is one of a small number of devices used in audio that can be called a transducer. Generally speaking, a transducer is any device that converts one kind of energy into another (for example, electrical energy into mechanical energy). In the case of microphones, we are converting mechanical energy (the movement of the air particles due to sound waves) into electrical energy (the output of the microphone). In order to choose and use your microphones effectively for various purposes, you should know a little about how this magical transformation occurs.
Back in the chapter on induction and transformers, we talked about an interesting relationship between magnetism and current. If you have a magnetic field, which is comprised of what we call magnetic lines of force all “pointing” in the same direction, and you move a piece of wire through it so that the wire cuts the lines of force perpendicularly, then you’ll generate a current in the wire. (If this is coming as a surprise, then you should read Chapters 2.6 and 2.7.)
Dynamic microphones rely on this principal. Somewhere inside the microphone, there’s a piece of metal or wire that’s sitting in a strong magnetic field. When a sound wave hits the microphone, it pushes and pulls on a membrane called a diaphragm that will, in turn, move back and forth proportionally to some component of the particle movement (either the pressure or the velocity – but we’ll talk more about that later). The movement of the diaphragm causes the piece of metal to move in the magnetic field, thus producing current that is representational of the movement itself. The result is an electrical representation of the sound wave where the electrical energy is actually converted from mechanical energy of the air molecules.
One important thing to note here is the fact that the current that is generated by the metal moving in the magnetic field is proportional to the velocity at which it’s moving. The faster it moves, the bigger the current. As a result, you’ll often hear dynamic microphones referred to as velocity microphones. The problem with this name is that some people like using the term “velocity microphone” to mean something completely unrelated – and as a result, people get very confused when you go from book to book and see the term in multiple places with multiple meanings. (For a further discussion on this topic, see the section on Pressure Gradient microphones in Section 6.7.)
The simplest design of dynamic transducer we can make is where the diaphragm is the piece of metal that’s moving in the magnetic field. Take a strip of aluminium a couple of μm (micrometers) thick, 2 to 4 mm wide and a couple of centimeters long and bend it so that it’s corrugated (see Figure 6.114) to make it a little stiff across the width. This will be the diaphragm of the microphone. It’s nice and light, so it moves very easily when the sound wave hits it. Now we’ll support the microphone from the top and bottom and hang it in between the north and south poles of a strong magnet as shown in Figure 6.114.
Referring to the construction in Figure 6.114: if a sound wave with a positive pressure hits the front of the diaphragm, it moves backwards and generates a current that goes up the length of the aluminium (you can double check this using the right hand rule described in Chapter 2.6). Therefore, if we connect wires that run from the top and bottom of the diaphragm out to a preamplifier, we’ll get a signal.
There are a couple of small problems with this design. Firstly, the current that’s generated by one little strip of aluminium that’s getting pushed back and forth by a sound wave will be very small. So small that a typical microphone preamplifier won’t have enough gain to bring the signal up to a useable level. Secondly, consider that the impedance of a strip of aluminium a couple of centimeters long will be very small, which is fine, except that the input of the microphone preamp is expecting to “see” an impedance which is at least around 200Ω or so. Luckily, we can fix both of these problems in one step by adding a transformer to the microphone.
The output wires from the diaphragm are connected to the primary coil of a transformer that steps up the voltage to the secondary coil. The result of this is that the output of the microphone is increased proportionally to the turns ratio of the transformer, and the apparent impedance of the diaphragm is increased proportionally to the square of the turns ratio. (See Section 2.7 of the electronics section if this doesn’t make sense.) So, by adding a small transformer inside the body of the microphone, we kill both birds with one stone. In fact, there is a third dead bird lying around here as well – we can also use the transformer to balance the output signal by including a centre tap on the secondary coil and making it the ground connection for the mic’s output. (See Chapter 6.5 for a discussion on balancing if you’re not sure about this.)
That’s pretty much it for the basic design of a ribbon dynamic microphone – different manufacturers will use different designs for their magnet and ribbon assembly. There is an advantage and a couple of disadvantages in this design that we should discuss at this point. Firstly, the advantage: since the diaphragm in a ribbon microphone is a very small piece of aluminium, it is very light, and therefore very easy to move quickly. As a result, ribbon microphones have a good high-frequency response characteristic (and therefore a good transient response). On the contrary, there are a number of disadvantages to using ribbon microphones. Firstly, you have to remember that the diaphragm is a very thin and relatively fragile strip of aluminium. you cannot throw a ribbon microphone around in a road case and expect it to work the next day – they’re just too easily broken. Since the output of the diaphragm is proportional to the its velocity, and since that velocity is proportional to frequency, the ribbon has a very poor low-frequency response. There’s also the issue of noise: since the ribbon itself doesn’t have a large output, it must be boosted in level a great deal, therefore increasing the noise floor as well. The cost of ribbon microphones is moderately high (although not insane) because of the rather delicate construction. Finally, as we’ll see a little later, ribbon microphones are particularly susceptible to low-frequency noises caused by handling and breath noise.
In the chapter on induction, we talked about ways to increase the efficiency of the transfer of mechanical energy into electrical energy. The easiest way to do this is to take your wire that’s moving in the magnetic field and turn it into a coil. The result of this is that the individual turns in the coil reinforce each other producing more current.
This same principal can be applied to a dynamic microphone. If we replace the single ribbon with a coil of copper wire sitting in the gap of a carefully constructed magnet, we’ll generate a lot more current with the same amount of movement. Take a look at Figures 6.115 and 6.116.
Now, when the coil is moved in and out of the magnet, a current is generated that is proportional to the velocity of the movement. How do we create this movement? We glue the front of the coil on to a diaphragm made of plastic as is shown in the cross section in Figure 6.116.
Pressure changes caused by sound waves hitting the front of the diaphragm push and pull it, moving the coil in and out of the gap. This causes the wire in coil to cut perpendicularly through the magnetic lines of force, thus generating a current that is substantially greater than that produced by the ribbon in a ribbon microphone.


This signal still need to be boosted, and the impedance of the coil isn’t high enough for us to simply take the wire connected to the coil and connect it to the microphone’s output. Therefore, we use a step-up transformer again, just as we did in the case of the ribbon mic, to increase the sigal strength, increase the output impedance to around 200Ω, and to provide a balanced output.
There are a number of advantages and disadvantages to using moving coil microphones. One of the biggest advantages is the rugged construction of these devices. For the most part, moving coil microphones border on being indestructible – in fact, it’s almost difficult to break one without intentionally doing so. This is why you’ll see them in road cases of touring setups – they can withstand a great deal of abuse. Secondly, since there are so many of these devices in production, and because they have a fairly simple design, the costs are quite affordable. On the side of the disadvantages, you have to consider that the coil in a moving coil microphone is relatively heavy and difficult to move quickly. As a result, it’s difficult to get a good high frequency response from such a microphone. Similarly, since the output of the coil is dependent on its velocity, very low frequencies will result in little output as well.
The goal in a microphone is to turn the movement of a diaphragm into a change in electrical potential. As we saw in dynamic microphones, this can be done using induction however, there is another way.
Take a balloon and rub it on your head (I’m assuming at this point that you have more hair than I...) If you put this balloon and place it on the side of your head, it will probably stick there. Why does this happen? When you rub the balloon on your hair, you transfer electrons out of it (and they wind up in you). We have already seen in Section 2.4 that a substance with a lack of electrons will be attracted to a substance with too many electrons. The more you rub the balloon on your head, the more electrons you’ll pull out of it, and the better it will stick to things.
If you were able to count the number of electrons that got removed from the balloon, you could measure its electric charge in coulombs. One Coulomb is equal to the charge of 6.24 x 1018 electrons. This is an interesting number that relates back to a number of different concepts that we have already seen in previous chapters.
For example, if you have 1 Ampere of current flowing through a wire, then this means that 6.24 x 1018 electrons flow through the wire each second. So, one coulomb is equal to one ampere per second as is shown in Equation 6.8
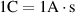 | (6.8) |
This also means the reverse – when 1 coulomb flows through a wire in 1 second, then the current is 1 Ampere.
If you have a capacitor with a capacitance of 1 farad, and you move 1 coulomb from one of its plates to the other, then the result will be a potential of 1 volt difference across the two plates. This is expressed in Equation 6.10.
At this point, you are probably wondering why we’ve been talking about balloons and coulombs in a section on microphones. Let’s go back to the balloon that you’ve rubbed on your head. If, instead of sticking the balloon back on your head, you bring it close to your arm, you’ll start to feel the hairs on your arm raising up to meet the balloon. The closer the balloon gets, the more you can feel it pulling.
This effect is something we discussed back in Section 2.4 on capacitors. Remember that the capacitance of a capacitor is partly dependent on the distance between its plates. The closer the plates get to each other, the higher the capacitance. Let’s now take Equation 6.10 and move things around a bit to produce Equation 6.11
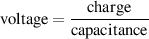 | (6.11) |
“So what?” I hear you cry. Well, if we take a capacitor and charge it to a fixed charge, and then change its capacitance by moving its plates closer together and further apart, then the voltage across the plates will change proportionally.
While this effect can be used to make the hairs on your arm stand up with a balloon, it can also be used to make a microphone. If one of the plates of the capacitor is a big chunk of metal that doesn’t move, and the other plate is a very lightweight, thin piece of metal that is able to move when a sound pressure wave hits it, then when the sound pressure moves the lighter plate (the microphone’s diaphragm) in and out, we’ll see a voltage change across the capacitor.
As we saw in Section 2.4, once upon a time, we used the name condensers instead of capacitors, which is why a microphone based on a capacitor is still called a condenser microphone.
Let’s look at a simple example of this. We’ll take a thin film of metal that’s usually circular, and stretch it like the head of a drum. Right behind that, we’ll put a flat, but thick circular piece of metal called a backplatewith a slightly smaller diameter than the diaphragm. These two make the plates of a capacitor. This capacitor is put in series with a DC voltage supply like a battery, for example, and a resistor as is shown in Figure 6.120.
So, what are all the components in this circuit doing? We have already seen that the movement of the diaphragm causes a change in the voltage across it. The battery is in the circuit to charge the capacitor – if it wasn’t there, then there would be no difference in the number of electrons in each plate of the capacitor. However, if we were to leave the resistor out of the circuit and just connect the battery to the capacitor, then the battery would hold the voltage across the capacitor to a constant level. So, the resistor allows the voltage across the capacitor to be different from the voltage across the battery. That difference is the voltage across the resistor, so we’ll just look at that voltage and use it as our output.
Let’s think about this in a little more detail. In the circuit in Figure 6.120, the diaphragm of the microphone will have a positive charge (because it’s directly connected to the positive terminal of the battery). If we connect the battery and wait for a while (for 5 time constants), then the voltage across the capacitor will eventually match the voltage across the battery and the voltage across the resistor will be 0 V. (The amount of time that this takes is dependent on the capacitance and the resistance as we learned back in Figure 2.13.) If a sound wave hits the diaphragm with a high pressure, it pushes the diaphragm closer to the backplate. This causes the capacitance to go up, and we’ll assume that the charge stays constant. (We can almost assure this by making the resistor really big, so the time constant of the RC circuit is really long compared to the period of a sound wave.) If the capacitance goes up and the charge stays constant than the voltage across the capacitor goes down and the voltage across the resistor goes up. If the sound pressure was low, then the diaphragm gets pulled away from the backplate and the reverse happens.
One important issue in this is the relationship between the capacitance of the diaphragm and backplate and the resistance of the resistor. This relationship determined the RC time constant of the entire circuit. If that time constant is too small, then the change in capacitance caused by the moving diaphragm will cause a change in charge as current “leaks” through the resistor into the capacitor. If the resistor is big enough, then that “leak” is very small, so the charge across the capacitor stays constant. Typically, the capacitance of the diaphragm and backplate is on the order of 10 picofarads and the resistance of the resistor is on the order of 100 MΩ or higher.
The voltage signal at the resistor is very small because the change in capacitance is very small. Consequently, we will have to amplify the signal considerably. It is not enough to simply put the resistor in parallel with a microphone preamplifier. Firstly, there is not enough gain in the mic preamp. Secondly, the output impedance of this circuit will not make a nice match for the input impedance of the preamp, which means that we’ll probably just wind up with a noisy, but quiet signal. So, we have to put a preamp after the resistor in this circuit, but before the microphone preamp in your mixing console. This preamp is usually an internal one made up of a circuit inside the body of the microphone. The internal preamp gives you gain, but also a nice output impedance and, in most cases, a balanced output that’s capable of driving a long-enough microphone cable.
Note that, if you’re a really clever microphone designer, then you’ll power the internal preamp using the same power source as the one you’re using to charge the capacitor.
In theory, if you rub a balloon on your head and charge it up, put it on a table and leave it there, you can come back tomorrow, or in a week, or a year, and the balloon will still be charged. Of course, in reality, that won’t be the case. In fact, if you come back in a year, the balloon will be a discharged and it will also be deflated. However, there are some materials that, after they have been charged, will keep that charge forever. Such a material is the electrical equivalent of a permanent magnet, which is why we call it an electret (an ELECTRicity magnET).
If you build a condenser microphone like the one shown in Figure 6.120, but you use an electret material for the diaphragm, then you don’t need to have the polarizing voltage to charge the capacitor. This is because the electret is permanently charged. The basic principle of operation is the same as in the case of a DC polarized condenser, so the only big change is the way the capacitor is charged.
Note, however, that electret microphones still need a power supply, either from some internal source like a battery, or an external source, however, this is just needed to power up the mic’s internal amplifier.
A little trivia: the electret condenser microphone was invented in 1962 by Jim West and Gerhard Sessler at Bell Labs. The first one was made using Teflon foil, so they called it the foil electret microphone. I once attended an interesting lecture by Dr. West at an AES convention. One of his comments during his speech was that he would have bet that there were more electret condenser microphones in the room at that moment than there were people. My gut reaction to this comment was that he was crazy, but when I realised that I, myself, was carrying at least 3 that I knew of (1 Macintosh laptop, 1 personal cell phone and 1 business cell phone), I realised that he was probably right.
Although the correct term is to call these microphones electret condenser, or even just electret microphones, they’re typically just thrown into the category of condenser mic’s. However, if you look in the details of your data sheet, it will tell you whether you have a DC polarized condenser or an electret microphone.
TO BE WRITTEN
If you take a look at any book of science experiments for kids you’ll find a project that teaches children about barometric pressure. You take a coffee can and stretch a balloon over the open end, sealing it up with rubber bands. Then you use some tape to stick a drinking straw on the balloon so that it hangs over the end.
So, what is this thing? Believe it or not, it’s a barometer. If the seal on the ballon is tight, then no air can escape from the can. As a result, if the barometric pressure outdoors goes down (when the weather is rainy), then the pressure inside the can is relatively high (relative to the outside, that is...) so the balloon swells up in the middle and the straw points down.
On a sunny day, the barometric pressure goes up and the balloon is pushed into the can, so the straw points up.
This little barometer tells us a great deal about how a microphone works. There are two big things to remember about this device:
The barometer in the introduction responds to large changes in barometric pressure on the order of 2 or 3 Pascals over long periods of time on the order of hours or days. However, if we made a miniature copy of the coffee can and the balloon, we’re have a device that would respond much more quickly to much smaller changes in pressure. In fact, if we were to call the miniaturized balloon a diaphragm and make it about 1 cm in diameter or so, it would be perfect for responding to changes in pressure caused by passing sound waves instead of passing weather systems.
So, let’s consider what we have. A small can, sealed on the front by a very thin diaphragm. This device is built so that the diaphragm moves in and out of the can with changes in pressure between 20 micropascals and 2 pascals (give or take...) and frequencies up to about 20 kHz or so. There’s just one problem: the diaphragm moves a distance that is proportionate to the amplitude of the pressure change in the air, so if the barometric pressure goes down on a rainy day, the diaphragm will get stretched out and will probably tear. So, to prevent this from happening, we’ll drill a very small hole called a capillary tube in the back of the can for very long term changes in the pressure. If you’d like to build one, the construction diagrams are shown in Figure 6.121.
The biologically-minded reader may be interested to note that this is essentially the construction of the human ear. The diaphragm is your eardrum, the canister is your head (or at least a small cavity behind your eardrum inside your head) and the capillary tube is your eustachian tube that connects the back of your eardrum to your mouth. When you undergo a wide change in air pressure in a longer period of time (like when you’re taking off in an airplane, for example), your eardrum is pushed out and “pops” just like the diaphragm would be. And, like the capillary tube, the eustachian tube lets the new pressure “equalize” on the back of the eardrum – therefore, by yawning or swallowing, you put your eardrum back where it belongs.
How will this system behave? Remember that, just like the coffee can barometer, the back of the diaphragm is effectively sealed so if the pressure outside the can is high, the diaphragm will get pushed into the can. If the pressure outside the can is low, then the diaphragm will get pulled out of the can. This will be true no matter where the change in pressure originated. (The capillary tube is of a small enough diameter that fast pressure changes in the audio range don’t make it through into the can through the tube, so we can consider the can to be completely sealed.)
What we have is called a pressure transducer. Remember that a transducer is any device that converts one kind of energy into another. In the case of a microphone, we’re converting mechanical energy (the movement of the diaphragm) into electrical energy (the change in voltage and/or current at the output). How that conversion actually takes place is dealt with in a previous chapter – what we’re concerned about in this chapter is the pressure part.
A perfect pressure transducer responds identically to a change in air pressure originating in any direction, and therefore arriving at the diaphragm from any angle of incidence. Every microphone has a “front,” “side” and “back,” but because we’re trying to be a little more precise about things (translation: because we’re geeks) we break this down further into angles. So, directly in front of the microphone is considered to be an angle of incidence of 0∘. We can rotate around from there to 90∘ on the side and 180∘ at the back as is shown in Figure 6.122.

We can make a graph of the way in which a perfect pressure transducer will respond to the pressure changes by graphing its sensitivity. This is a word used for the gain of a microphone caused by the angle of incidence of the incoming sound (although, as we saw earlier, other issues are included in the sensitivity as well). Remember in the case of a perfect pressure transducer, the sensitivity will be the same regardless of the angle of incidence, so if we consider that the gain for a sound source that’s on-axis or with an angle of incidence of 0∘ is normalized to a value of 1, then all other angles of incidence will be 1 as well. This can be plotted on a cartesian X-Y graph as is shown in Figure 6. The equation below can be used to calculate the sensitivity for a pressure transducer. (Okay, okay, it’s not much of an equation – for any angle, the sensitivity is 1...)
 | (6.12) |
where SP is the sensitivity of a pressure transducer.
For any angle, you can just multiply the pressure by the sensitivity for that angle of incidence to find the voltage output.
Most people like to see this in a little more intuitive graph called a polar plot shown in Figure 6.124. In this kind of graph, the sensitivity is graphed as a radius from the centre of the graph at a given angle of rotation.
One thing to note here: most books plot their polar plots with 0∘ pointing directly upwards (towards 12 o’clock). Technically speaking, this is incorrect – a proper polar plot starts with 0∘ on the right side (towards 3 o’clock). This is the system that I’ll be using for all polar plots in this book.
Just for the sake of having a version of the plots that look nice and clean, Figures 6.125 and 6.127 are duplicates of Figures 6.123 and 6.124.
Most people don’t call these microphones “pressure transducers” – because the microphone is equally sensitive to all sound sources regardless of direction they’re normally called omnidirectional microphones. Some people shorten this even further and call them omni’s.
What happens if the diaphragm is held up in mid-air without being sealed on either side? Figure 6.128 shows just such a system where the diaphragm is supported by a ring and is exposed to the outside world on both sides.
Let’s assume for the purposes of this discussion that a movement of the diaphragm to the left of the resting position somehow magically results in a positive voltage at the output of this microphone (for more info on how this miracle actually occurs, read Section 6.6.) Therefore if the diaphragm moves in the opposite direction, the voltage at the output will be negative. Let’s also assume that the side of the diaphragm facing the right is called the “front” of the microphone.
If there’s a sound source producing a high pressure at the front of the diaphragm, then the diaphragm is pushed backwards and the voltage output is positive. Positive pressure causes positive voltage. If the sound source stays at the front and produces a low pressure, then the diaphragm is pulled frontwards and the resulting voltage output is negative. Negative pressure causes negative voltage. Therefore there is a positive relationship between the pressure at the front of the diaphragm and the voltage output – meaning that, the polarity of the voltage at the output is the same as the pressure at the front of the microphone.

What happens if the sound source is at the rear of the microphone at an angle of incidence of 180∘? Now a positive pressure pushes on the diaphragm from the rear and causes it to move towards the front of the microphone. Remember from two paragraphs back that this causes a negative voltage output. Positive pressure causes negative voltage. If the source is in the rear and the pressure is negative, then the diaphragm is pulled towards the rear of the microphone, resulting in a positive voltage output. Now, we have a situation where there is a negative relationship between the pressure at the rear of the microphone and the voltage output – the polarity of the voltage at the output is opposite to the pressure at the rear.
What happens when the sound source is at an angle of incidence of 90∘ – directly to one side of the microphone? If the source produces a high pressure, then this reaches both sides of the diaphragm equally and therefore the diaphragm doesn’t move. The result is that the output voltage is 0 – there is no output. The same will be true if the pressure is negative because the two low-pressure areas on either side of the microphone will be pulling equally on the diaphragm.
This phenomenon of the sound source outputting a high or low pressure with no voltage at the output of the microphone shows exactly what’s happening in this microphone. The movement of the diaphragm (and therefore the output of the microphone) is dependent on the difference in pressure on the two sides of the diaphragm. If the pressure on the two sides is the same, the difference is 0 and therefore the output is 0. The bigger the difference in pressure, the bigger the voltage output. Another word for “difference” is “gradient” and thus this design is called a Pressure Gradient Transducer.
We know the sensitivity of the microphone at four angles of incidence – at 0∘ the sensitivity is 1 just like a Pressure Transducer. At 180∘, the sensitivity is -1. The voltage waveform will look like the pressure waveform, but it will be upside down – inverted in polarity because it’s multiplied by -1. At 90∘ and 270∘ the sensitivity will be 0 – no matter what the pressure is, the voltage output will be 0.
The question now is, what happens at all the other angles? Well, it might be already obvious. There’s a simple function that converts angles to a number where 0∘ corresponds to a value of 1, 90∘ to 0, 180∘ to -1 and 270∘ to 0 again. The function is called a cosine – it turns out that the sensitivity of this construction of microphone is the cosine of the angle of incidence as is shown in Figure 6.131. So, the equation for calculating the sensitivity is:
 | (6.13) |
where SG is the sensitivity of a pressure gradient transducer and α is the angle of incidence.
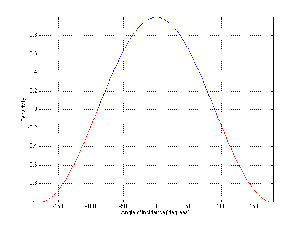
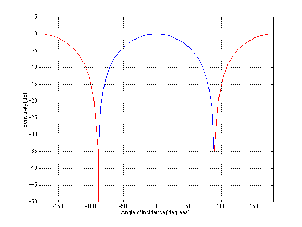
Again, most people prefer to see this in a polar plot as is shown in Figure 6.134, however, what most people don’t know is that they’re not really looking at an accurate polar plot of the sensitivity. In this case, we’re looking at a polar plot of the absolute value of the cosine of the angle of incidence (if this doesn’t make sense, don’t worry too much about it).
Notice that in the graph in Figure 6.134, the front half of the plot is in blue while the rear half is red. This is to indicate the polarity of the sensitivity, so at an angle of 180∘, the radius of the plot is 1, but because the plot at that angle is red, it’s -1. At 30∘, the radius is 0.5 and because it’s blue, then it’s positive.
Just like pressure transducers are normally called omnidirectional microphones, pressure gradient transducers are usually called either bidirectional microphones (because they they’re sensitive in two directions – the front and back) or figure eight microphones (because the polar pattern looks like the number 8).
There’s one thing that we should get out of the way right now. Many people see the figure 8 pattern of a bidirectional microphone and jump to the assumption that the mic has two outputs – one for the front and one for the back. This is not the case. The microphone has one output and one output only. The sound picked up by the front and rear lobes is essentially mixed acoustically and output as a single signal. You cannot separate the two lobes to give you independent outputs.
It is possible to create a microphone that has some combination of both a pressure component and a pressure gradient component. For example, look at the diagram in Figure 6.135. This shows a microphone where the diaphragm is not entirely sealed in a can as in the pressure transducer design, but it’s not completely open as in the pressure gradient design.
In this case, the path to the back of the diaphragm from the outside world is the same length as the path to the front of the diaphragm when the sound source is at 180∘ – not 90∘ as in a pure pressure gradient transducer. This then means that there will be no output when the sound source is at the rear of the microphone. In this case, the sensitivity pattern is created by creating a mixture of 50% Pressure and 50% Pressure Gradient. Therefore, we’re multiplying the two pure sensitivity patterns by 0.5 and adding them together. This results in the pattern shown in Figure 6.136 – notice the similarity between this pattern and the perfect pressure gradient sensitivity pattern – it’s just a cosine wave that’s been offset by enough to eliminate the negative components.
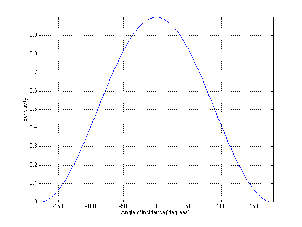

If we plot this sensitivity pattern on a polar plot, we get the graph shown in Figure 6.138. Notice that this pattern looks somewhat like a heart shape, so it’s normally called a cardioid pattern (“cardio” meaning “heart” as in “cardio-vascular” or “cardio-pulmonary”)
We can now develop a general equation for calculating the sensitivity pattern of a microphone that contains both Pressure and Pressure Gradient components as follows:
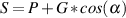 | (6.14) |
where S is the sensitivity of the microphone, P is the Pressure component, G is the Pressure Gradient component, α is the angle of incidence and where P + G = 1.
For example, for a microphone that is 50 percent Pressure and 50 percent Pressure Gradient, the sensitivity equation would be:
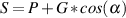 | (6.15) |
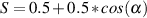 | (6.16) |
This sensitivity equation can then be used to create any polar pattern between a perfect pressure transducer and a perfect pressure gradient. All we need to do is to decide how much of each we want to add in the equation. For a perfect omnidirectional microphone, we make P=1 and G=0. Therefore the microphone is a 100 percent pressure transducer and 0 percent pressure gradient transducer. There are five “standard” polar patterns, although one of these is actually two different standards, depending on the manufacturer. The five most commonly-seen polar patterns are:
| Polar Pattern | P | G |
| Omnidirectional | 1 | 0 |
| Subcardioid | 0.75 | 0.25 |
| Cardioid | 0.5 | 0.5 |
| Supercardioid | 0.333 | 0.666 |
| Hypercardioid | 0.25 | 0.75 |
| Bidirectional | 0 | 1 |
What do these polar patterns look like? We’ve aready seen the omnidirectional, cardioid and bidirectional patterns. The others are shown in Figures 6.139 through 6.147.
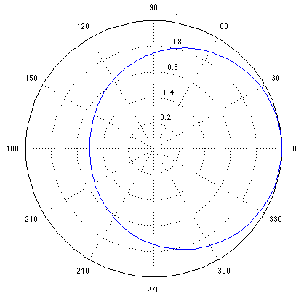
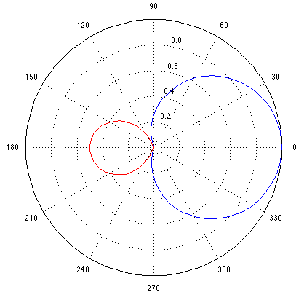
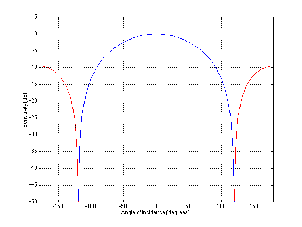
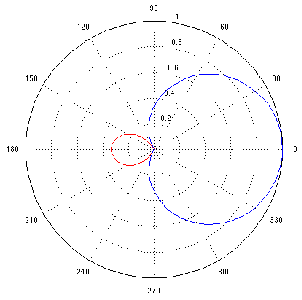
Just to compare the relationship between the various directional patterns, we can look at all of them on the same plot. This gets a little complicated if they’re all on the same polar plot – just because things get crowded, but if we see them on the same Cartesian plot (see the graphs above for the corresponding polar plots) then we can see that all of the simple directional patterns are basically the same.
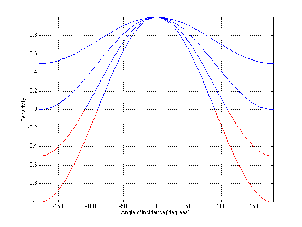
One of the interesting things that becomes obvious in this plot is the relationship between the angle of incidence where the sensitivity is 0 – sometimes called the null because there is no output – and the mixture of the Pressure and Pressure Gradient components. All mixtures between omnidirectional and cardioid have no null because there is no angle of incidence that results in no output. The cardioid microphone has a single null at 180∘, or, directly to the rear of the microphone. As we increase the mixture to have more and more Pressure Gradient component, the null splits into two symmetrical points on the polar plot that move around from the rear of the microphone to the sides until, when the transducer is a perfect bidirectional, the nulls are at 90 and 270∘.
If you go to your local microphone store and buy a “normal” single-diaphragm cardioid microphone (don’t worry if you’re surprised that there might be something other than a microphone with a single diaphragm... we’ll talk about that later) the manufacturer has built the device so that it’s the appropriate mixture of Pressure and Pressure Gradient. Consider, however, that if you have a perfect omnidirectional microphone and a perfect bidirectional microphone, then you could strap them together, mix their outputs electrically in a run-of-the-mill mixing console, and, assuming that everything was perfectly aligned, you’d be able to make your own cardioid. In fact, if the two real microhpones were exactly matched, you could make any polar pattern you wanted just by modifying the relative levels of the two signals.
Mathematically speaking, the output of the omnidirectional microphone is the Pressure component and the output of the Bidirectional Microphone is the Pressure Gradient component. The two are just added in the mixer so you’re fulfilling the standard sensitivity equation:
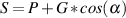 | (6.17) |
where P is the gain applied to the omnidirectional microphone and G is the gain applied to the bidirectional microphone.
Also, let’s say that you have two cardioid microphones, but that you put them in a back-to-back configuration where the two are pointing 180∘ away from each other. Let’s look at this pair mathematically. We’ll call microphone 1 the one pointing “forwards” and microphone 2 the second microphone pointing 180∘ away. Note that we’re also assuming for a moment that the gain applied to both microphones is the same.
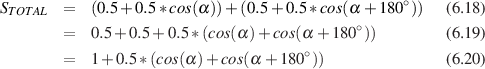
Now, consider that the cosine of every angle is the opposite polarity to the cosine of the same angle + 180∘. In other words:
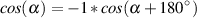 | (6.21) |
Therefore the cosine of any angle added to the cosine of the same angle + 180∘ will equal 0. In other words:
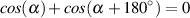 | (6.22) |
Let’s go back to the equation that describes the back to back cardioids:
 | (6.23) |
We now know that the two cosines cancel each other, therefore the equation simplifies to:
Therefore, the result is an omnidirectional microphone. This result is possibly easier to understand intuitively if we look at graphs of the sensitivity patterns as is shown in Figures 6.149 and 6.150.
Similarly, if we inverted the polarity of the rear-facing microphone, the resulting mixed output (if the gains applied to the two cardioids were equal) would be a bidirectional microphone. The equation for this mixture would be:
So, as you can see, not only is it possible to create any microphone polar pattern using the summed outputs of a bidirectional and an omnidirectional microphone, it can be accomplished using two back-to-back cardioids as well. Of course, we’re still assuming at this point that we’re living in a perfect world where all transducers are matched – but we’ll stay in that world for now...
Remember that a pressure transducer is basically a sealed can, just like the coffee can barometer described in Section 6.7.1. Therefore, any change in pressure in the outside world results in the displacement of the diaphragm. High pressure pushes the diaphragm in, low pressure pulls it out. Unless the change in pressure is extremely slow with a period on the order of hours (which we obviously will not hear as a sound wave – and which leaks through the capillary tube) then the displacement of the diaphragm is dependent on the pressure, regardless of frequency. Therefore a perfect pressure transducer will respond to all frequencies similarly. This is to say that, if a pressure wave arriving at the diaphragm is kept at the same peak pressure value, but varied in frequency, then the output of the microphone will be a voltage waveform that changes in frequency but does not change in peak voltage output.
A graph of this would look like Figure 6.151.

The behaviour of a Pressure Gradient transducer is somewhat different because the incoming pressure wave reaches both sides of the diaphragm. Remember that the lower the frequency, the longer the wavelength. Also, consider that, if a sound source is on-axis to the transducer, then there is a path length difference between the pressure wave hitting the front and the rear of the diaphragm. That path length difference remains at a constant delay time regardless of frequency, therefore, the lower the frequency the more alike the pressures at the front and rear of the diaphragm because the phase difference is smaller with lower frequencies. The delay is constant and short because the diaphragm is typically small.
Since the sensitivity at the rear of the diaphragm has a negative polarity and the front has a positive polarity, then the result is that the pressure at the rear is subtracted from the front.
With this in mind, let’s start at a frequency of 0 Hz and work our way upwards. At 0 Hz, then the pressure at the rear of the diaphragm equals the pressure at the front, therefore the diaphragm does not move and there is no output. (Note that, right away, we’re looking at a different beast than the perfect Pressure transducer. Without the capillary tube, the pressure transducer would give us an output with a 0 Hz pressure applied to it.)
As we increase in frequency, the phase difference in the pressure wave at the front and rear of the diaphragm increases. Therefore, there is less and less cancellation at the diaphragm and we get more and more output. In fact, we get a doubling of output for every doubling of frequency – in other words, we have a slope of +6 dB per octave.
Eventually, we get to a frequency where the pressure at the rear of the microphone is 180∘ later than the pressure at the front. Therefore, if the pressure at the front of the microphone is high and pushing the diaphragm in, then the pressure at the rear is low and pulling the diaphragm in. At this frequency, we have constructive interference and an increased output by 6 dB.
If we increase the frequency further, then the phase difference between the front and rear increases and we start approaching a delay of 360∘. At that frequency (which will be twice the frequency where we had +6 dB output) we will have no output at all – therefore a level of -∞ dB.
As the frequency increases, we result in a common pattern of peaks and valleys shown in Figure 6.153.
The frequencies of the peaks and valleys in the frequency response are determined by the distance between the front and the rear of the diaphragm. This distance, in turn, is principally determined by the diameter of the diaphragm. The smaller the diameter, the shorter the delay and the higher the frequency of the lowest-frequency peak.
Most manufacturers build their bidirectional microphones so that the lowest frequency peak in the frequency response is higher than the range of normal audio. Therefore, the “standard” frequency response of a bidirectional microphone starts an output of 0 at 0 Hz and doubles for every doubling of frequency to a maximum output that is somewhere around or above 20 kHz.
This, of course, is a problem. We don’t want a microphone that has a rising frequency response, so we have to fix it. How? Well, we just build the diaphragm so that it has a natural resonance down in the low frequency range. This means that, if you thump the diaphragm like a drum head, it will ring at a very low note. The higher the frequency, the further you get from the peak of the resonance. This resonance acts like a filter that has a gain that increases by 6 dB for every halving of frequency. Therefore, the lower the frequency, the higher the gain. This counteracts the rising natural slope of the diaphragm’s output and produces a theoretically flat frequency response. The only problem with this is that, at very low frequencies, there is almost no output to speak of, so we have to have enormous gain and the resulting output is basically nothing but noise.

The moral of this story is that Pressure Gradient microphones have no very-low-frequency output. Also, keep in mind that any microphone with a Pressure Gradient component will have a similar response. Therefore, if you want to record program material with very-low-frequency content, you have to stick with omnidirectional microphones.
Most microphones that have a pressure gradient component have a correction filter built in to fix the low frequency problems of the natural response of the diaphragm. In many cases, this correction works very well, however, there is a specific case where the filter actually makes things worse.
Consider that a pressure gradient microphone has a naturally rising frequency response because the incoming pressure wave arrives at the front as well as at the rear of the diaphragm. Pressure microphones have a naturally flat frequency response because the rear of the diaphragm in sealed from the outside world. Also, consider a little rule of thumb that says that, in a free, unbounded space, the pressure of a sound wave is reduced by half for every doubling of distance. The implication of this rule is that, if you’re very close to a sound source, a small change in distance will result in a large change in sound level. At a greater distance from the sound source, the same change in distance will result in a smaller change in level. For example, if you’re 1 cm from the sound source, moving away by 1 cm will cut the level by half, a drop of 6 dB. If you’re 1 m from the sound source, moving away by 1 cm will have a negligible effect on the sound level. So what?
Imagine that you have a pressure gradient microphone that is placed very close to a sound source. Consider that the distance from the sound source (say, a singer’s mouth...) to the front of the diaphragm will be on the order of millimeters. At the same time, the distance to the rear of the diaphragm will be comparatively very far – possibly 4 to 8 times the distance to the singer’s lips. Therefore there is a very large drop in pressure for the sound wave arriving at the rear of the diaphragm. The result is that the rear of the diaphragm is effectively sealed from the outside world by virtue of the fact that the sound pressure level at that side of the diaphragm is much lower than that at the front. Consequently, the natural frequency response becomes more like a pressure transducer than a pressure gradient transducer.
What’s the problem? Well, remember that the microphone has a filter that boosts the low end built into it to correct for problems in the natural frequency response – problems that don’t exist when the microphone is close to the sound source. As a result, when the microphone is very close to the source, there is a boost in the low frequencies because the correction filter is applied to a now naturally flat frequency response. This boost in the low end is called proximity effect because it is caused by the microphone being in close proximity to the sound source.
There are a number of microphones that rely on the proximity effect to boost the low frequency components of the signal. These are typically sold as vocal mic’s such as the Shure SM58. If you measure the frequency response of such a microphone from 1 m away, then you’ll notice that there is almost no low-end output. However, in typical usage, there is plenty of low end. Why? Because, in typical usage, the microphone is stuffed in the singer’s mouth – therefore there’s lots of low end because of proximity effect.
Remember, when the microphone has a pressure gradient component, the frequency response is partially dependent on the distance to the diaphragm. Also remember that, for some microphones, you have to be placed close to the source to get a reasonably low frequency response, whereas other microphones in the same location will have a boosted low frequency response.
As we saw in Section 6.1, the bandwidth of a filter is determined by the frequency band limited by the points where the signal is 3 dB lower than the maximum output of the filter. Microphones have a spatial equivalent called the acceptance angle. This is the frontal angle of the microphone where the sensitivity is within 3 dB of the on-axis response. This angle will vary with polar pattern.
In the case of an omnidirectional, all angles of incidence have a sensitivity of 0 dB relative to the on-axis response of the microphone. Consequently, the acceptance angle is ±180∘ because the sensitivity never drops below -3 dB relative to the on-axis sensitivity.
A subcardioid, on the other hand, has a sensitivity that drops below -3 dB when the angle of incidence of the sound source is outside the acceptance angle of ±99.9∘. A cardioid has an acceptance angle of ±65.5∘, a hypercardioid has an acceptance angle of ±52.4∘, and a bidirectional has an acceptance angle of ±45.0∘.
| Polar Pattern (P : G) | Acceptance Angle |
| Omnidirectional (1 : 0) | ±180∘ |
| Subcardioid (0.75 : 0.25) | ±99.9∘ |
| Cardioid (0.5 : 0.5) | ±65.5∘ |
| Supercardioid (0.375 : 0.625) | ±57.9∘ |
| Hypercardioid (0.25 : 0.75) | ±52.4∘ |
| Bidirectional (0 : 1) | ±45.0∘ |
Think about an omnidirectional microphone in a diffuse field (the concept of a diffuse field is explained in Section 3.1.22). The omni is equally sensitive to all sounds coming from all directions, giving it some output level. If you put a cardioid microphone in exactly the same place, you wouldn’t get as much output from it because, although it’s as sensitive to on-axis sounds as the omni, all other directions will be attenuated in comparison.
Since a diffuse field is comprised of random signals coming from random directions, we call the theoretical power output of a microphone in a diffuse field the Random-Energy Response or RER. Note that this measurement is of the power output of the microphone.
The easiest way to get an intuitive understanding of the RER of a given polar pattern is that it is simply the square of the surface area of a three-dimensional plot of the pattern. The reason we square the surface area is that we are looking at the power of the output which, as we saw in Section 2.1.4, is the square of the signal.
The RER of any polar pattern can be calculated using Equation 6.31.
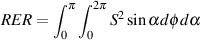 | (6.31) |
where S is the sensitivity of the microphone, α is the angle of rotation around the microphone’s “equator” and ϕ is the angle of rotation around the microphones axis. These two angles are shown in the explanation of spherical coordinates later in the book in Section 10.4.2.
If you’re having some difficulties grasping the intricacies of Equation 6.31, don’t panic. Double integrals aren’t something we see every day. We know from Section 1.9 that, because we’re dealing with integrals, then we must be looking for the area of some shape. So far so good. (The area we’re looking for is the surface area of the three-dimensional plot of the polar pattern.)
FINISH THIS OFF
There are a couple of good rules of thumb to remember when it comes to RER.
COMMENT HERE ABOUT REVERBERATION AND DIRECT TO REVERBERANT RATIOS
| Polar Pattern (P : G) | RER | RER (decimal) |
| Omnidirectional (1 : 0) | 4π | 12.57 |
| Subcardioid (0.75 : 0.25) | 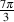 | 7.33 |
| Cardioid (0.5 : 0.5) | 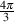 | 4.19 |
| Supercardioid (0.375 : 0.625) | 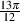 | 3.40 |
| Hypercardioid (0.25 : 0.75) | π | 3.14 |
| Bidirectional (0 : 1) | 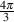 | 4.19 |
It’s a little difficult to remember the strange numbers that the RER equation comes up with, so we rarely bother. Instead, it’s really more interesting to see how the various microphone polar patterns compare to each other. So, what we do is call the RER of an omnidirectional the “reference” and then look at how the other polar patterns’ RER’s compare to it.
This relationship is called the Random-Energy Efficiency, abbreviated REE of the microphone, and is calculated using Equation 6.32.
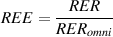 | (6.32) |
So, as we can see, all we’re doing is calculating the ratio of the microphone’s RER to that of an omni. As a result, the lower the RER, the lower the REE.
This value can be expressed either as a linear value, or it can be calculated in decibels using Equation 6.33.
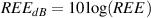 | (6.33) |
Notice in Equation 6.33 that we’re multiplying by 10 instead of the usual 20. This is because the REE is a power measurement and for power you multiply by 10 instead of 20.
In the practical world, this value gives you an indication of the relative outputs of microphone (assuming that they have similar electrical sensitivities) when you put them in a reverberant field. Let’s say that you have an omnidirectional microphone in the back of a concert hall to pick up some of the swimmy reverberation sound. If you replace it with a hypercardioid in the same location, you’ll have to crank up the gain of the hypercardioid by 6 dB to get the same output as the omni because the REE of a hypercardioid is - 6 dB.
| Polar Pattern | (P : G) | REE | REE (dB) |
| Omnidirectional | (1 : 0) | 1 | 0 dB |
| Subcardioid | (0.75 : 0.25) | 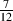 | -2.34 dB |
| Cardioid | (0.5 : 0.5) | 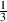 | -4.77 dB |
| Supercardioid | (0.375 : 0.625) | 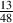 | -5.67 dB |
| Hypercardioid | (0.25 : 0.75) | 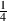 | -6.02 dB |
| Bidirectional | (0 : 1) |  | -4.77 dB |
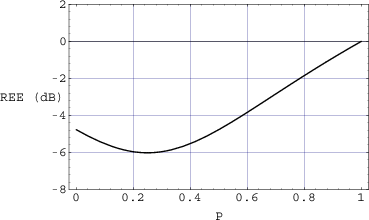
Of course, usually microphones (at least for classical recordings in reverberant spaces...) are not just placed far away in the back of the hall. Then again, they’re not stuck up the musicians’... uh... down the musicians’ throats, either. They’re somewhere in between where they’re getting a little direct sound, possibly on-axis, and some diffuse, reverberant sound. So, one of the characteristics we’re interested in is the relationship between these two signals. This specification is called the directivity factor (the DRF) of the microphone. It is the ratio of the response of the microphone in a diffuse field to the response to a free-field source with the same intensity as the diffuse field signal, located on-axis to the microphone. In essence, this is a measure of the direct-to-reverberant ratio of the microphone’s polar pattern.
Since
we can calculate the DRF using Equation 6.34
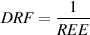 | (6.34) |
| Polar Pattern | (P : G) | DRF | Decimal equivalent |
| Omnidirectional | (1 : 0) | 1 | 1 |
| Subcardioid | (0.75 : 0.25) |  | 1.71 |
| Cardioid | (0.5 : 0.5) | 3 | 3 |
| Supercardioid | (0.375 : 0.625) |  | 3.69 |
| Hypercardioid | (0.25 : 0.75) | 4 | 4 |
| Bidirectional | (0 : 1) | 3 | 3 |
We can use the DRF to get an idea of the relative powers of the direct and reverberant signals coming from the microphones. Essentially, it tells us the relative sensitivities of those two signals, but what use is this to us in a panic situation when the orchestra is sitting out there waiting for you to put up the microphones and $1000 per minute is going by while you place the mic’s... It’s not, really... so we need to translate this number into a useable one in the real world.
Consider a couple of things:
So, we now have a question. If you have a sound source in a reverberant space, and you put an omnidirectional microphone somewhere in front of it, and you want a cardioid to have the same direct-to-reverberant ratio as the omni, where do you put the cardioid? If you put the two microphones side-by-side, the cardioid will sound closer since it will get the same direct sound, but less reverberant energy than the omni. Therefore, the cardioid must be placed farther away, but how much farther? This is actually quite simple to calculate. All we have to do is to convert the DRF (which is a measurement based on the power output of the microphone) into a Distance Factor (or DSF). This is done by coming back from the power measurement into an amplitude measurement (because the distance to the sound source is inversely proportional to the relative level of the received direct sound. In other words, if you go twice as far away, you get half the amplitude.) So, we can calculate the DSF using Equation 6.35.
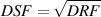 | (6.35) |
| Polar Pattern | (P : G) | DSF | Decimal equivalent |
| Omnidirectional | (1 : 0) | 1 | 1 |
| Subcardioid | (0.75 : 0.25) | 2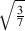 | 1.31 |
| Cardioid | (0.5 : 0.5) | 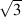 | 1.73 |
| Supercardioid | (0.375 : 0.625) | 4 | 1.92 |
| Hypercardioid | (0.25 : 0.75) | 2 | 2 |
| Bidirectional | (0 : 1) |  | 1.73 |
So, what does this mean? Have a look at Figure 6.163. All of the microphones in this diagram will have the same direct-to-reverberant outputs. The relative distances to the sound source have been directly taken from Table 6.10 as you can see...
WRITE THIS SECTION
INCLUDE CIRCUIT DIAGRAM
Thanks to Brian Madsen at Bang & Olufsen for his help in creating the colour 3D drawings of the loudspeaker in this section.
A loudspeaker is basically comprised of two things:
We can group the different types of loudspeaker drivers into two main categories:
There are other, more rare and esoteric systems that we will not discuss here, other than mentioning them... Some of these are, in no particular order:
As we have now seen many times, if you put current through a piece of wire, you generate a magnetic field around it. If that wire is suspended in another magnetic field, then the field that you generate will cause the wire to move. The direction of movement is determined by the polarity of the field that you created using the current in the wire. The velocity of the movement is determined by the strength of the magnetic fields, and therefore the amount of current in the wire.
Ribbon loudspeakers use exactly this principle. We suspend a piece of corrugated metal (typically aluminum) in a magnetic field and connect a lead wire to each end of the ribbon as is shown in Figure 6.164.
When we apply a current through the wire and ribbon, we generate a magnetic field, and the ribbon moves. If the current alternates between positive and negative, then the ribbon moves forwards and backwards respectively. Therefore, we have a loudspeaker driver where the ribbon itself is the diaphragm of the loudspeaker.
This ribbon has a low mass, so it’s easy to move quickly (making it appropriate for high frequencies) but it doesn’t create a large magnetic field, so it cannot play very loudly.. Also, if you thump the ribbon with your finger, you’ll see that it has a very low resonant frequency, mainly because it’s loosely suspended. As a result, this is a good driver to use for a tweeter, but it’s difficult to make it behave for lower frequencies.
There are advantages and disadvantages to using ribbon loudspeakers:
Think back to the chapter on electromagnetism and remember the right hand rule. If you put current though a wire, you’ll create a magnetic field surrounding it. Likewise if you move a wire in a magnetic field, you’ll induce a current. A moving coil loudspeaker relies on this property using a coil of wire suspended in a stationary magnetic field provided by a permanent magnet. If you send current though the coil, it induces a magnetic field around the coil (just like in a transformer). Since the coil is suspended, it is free to move, which is does according to the relationship of the strengths and directions of the two magnetic fields (the permanent one and the induced one). The bigger the current, the bigger the field, therefore the greater the movement.
Figure 6.165 shows a coil of wire that is about to be sunk into an oddly-shaped magnet. You can think of the lines of magnet force in the permanent magnet going from the north pole (the rod in the centre) to the south pole (the inside of the pipe). When the coil of wire is inserted into the groove cut in the magnet, it is sitting in the magnet’s field. If we put current in the coil, it will generate its own magnetic field whose strength is dependent on how much current we’re putting in, and whose polarity is dependent on in which direction it’s flowing. In real loudspeakers, the magnet looks like a hockey puck with a hole drilled in the middle. A piece of soft iron called the top plate is connected to the top of the magnet. There is a second piece called the bottom plate connected to the top of the magnet. Connected to the bottom plate (sometimes it’s the same piece of metal) is a soft iron cylinder called the pole piece coming up through the hole in the magnet.
As you already know, if you put two magnets in each other’s fields, you will get physical attraction or repulsion. Since we are going to use a really heavy permanent magnet in this case, and the coil of wire is suspended so that it’s free to move in or out, then as soon as we apply a current to the coil, it moves.
This is the basis for the movement behind all moving coil dynamic loudspeakers. Now all we have to do is sort out how to build one.
The first thing we have to do is to keep the coil (which, from now on, we’ll call the voice coil ) cylindrical. That’s accomplished by wrapping the wire around a tube that’s usually made of cardboard. That tube is called the former. In the manufacturing process, the wire (which has a very thin insulative coating on it) is wrapped around the former.
The voice coil and former are going to be moving in and out of the magnetic field with the changes in current that we apply to the voice coil. The goal here is to use that movement to change the air pressure in front of the loudspeaker driver, so we’ll need something to push and pull the air. That is accomplished by two things, a dust cap, which is a cap covering the open front end of the former, and a diaphragm or cone, which is a conical shaped plate with a hole in the middle. The outside edge of the dust cap glues to the inside edge of the hole in the diaphragm. It will likely also glue to the outside edge of the dust cap (however, in some drivers, the dust cap is glued to the face of the cone).
Next we have to suspend the whole thing so that the former and voice coil sit in the magnet with the diaphragm and dust cap in the front. The voice coil has to be free to move in and out of the magnet, but not sideways because it can’t be allowed to touch the magnet. This is accomplished using something called the loudspeaker’s suspension which is comprised of two things: a surround and a spider.
Take a look at Figure 6.175 to see how these two parts of the suspension are connected.
As you can see, the spider, which is usually a corrugated, circular disc, is glued to the top of the former and extends out to the metal holding the whole thing together, called the basket. This spider can stretch a little, allowing the former and voice coil to move in and out of the magnet (up and down in Figure 6.175). However, if only the spider were holding the rest in place, it could rock sideways as it moved in and out. So, we put another stretchy bit of material holding the outside edge of the diaphragm to the inside rim of the basket. This stretchy bit is called the surround and is usually made of rubber, foam or fabric.
Just to make things a little clearer, I took a typical-looking moving coil loudspeaker and cut it apart (don’t feel bad... it was a reject from a quality control check, so I found it in the garbage). This is shown in Figures 6.176.
A similar, but different loudspeaker, cut apart by the manufacturer is shown in 6.177 and 6.178. Notice that this second loudspeaker doesn’t have a separate surround and spider. They are one and the same in this particular case.
In order for the system to work well, you need reasonably strong magnetic fields. The easiest way to do this is to use a really strong permanent magnet. You could also improve the packing density of the voice coil. This essentially means putting more metal in the same space by changing the cross-section of the wire. The close-ups shown below illustrate how this can be done. The third (and least elegant) method is to add more wire to the coil. Later, we’ll talk about why this is probably bad idea.
Loudspeakers have to put a great deal of acoustic energy into a room, so they have to push a great deal of air. This can be done in one of two ways:
In the first case, you have to move a big mass (the diaphragm and the air next to it) by a little, in the second case, you move a little mass by a lot – either way you need to get a lot of energy into the room. If the loudspeaker is inefficient, you’ll be throwing away large amounts of energy produced by your power amplifier. This is why you worry about things like packing density of the voice coil. If you try to solve the problem simply by making the voice coil bigger (by adding more wire), you also make it heavier, and therefore harder to move.
There are advantages and disadvantages to using moving coil loudspeakers:
When we learned how capacitors worked, we talked a bit about electrostatic attraction. This is the tendency for oppositely charged particles to attract each other, and similarly charged particles to repel each other. This is what causes electrons in the plates of a capacitor to bunch up when there’s a voltage applied to the device. Let’s now take this principle a step farther.
Charge the middle plate with a DC polarizing voltage. It is now equally attracted to the two outside plates (assuming that their charges are equal).
If we change the charge on the outside plates such that they are different from each other, the inside plate will move towards the plate of more opposite polarity.
If we then perforate the plates (or better yet, make them out of a metal mesh) the movement of the inside plate will cause air pressure changes that radiate through the holes into the room.
There are (as expected) advantages and disadvantages to this system.
In the last chapter, we looked at the various parts of a typical moving coil loudspeaker and how they work on an intuitive level. However, in order to understand them at a deeper level, we’re going to have to dig...
Think about a moving coil loudspeaker at its simplest level. It has a mass (comprised mostly of the voice coil, the former, dust cap and diaphragm). That mass is suspended by a spring (the suspension, comprised of the surround and the spider.) If you have a mass on a spring, then you have a resonant system (we saw this back in Section 3.1.2) The inertia of the mass wants to keep doing what it’s doing (i.e. it wants to keep moving if it’s already moving) and the stiffness of the spring wants it to be in one place (so it wants to either pull the mass back, or push it out to its resting place). When things are moving, these two forces are opposite in polarity (see Section 3.1.24 where we talked about this with dinner plates as the analogy) and result in the whole thing resonating at some single frequency. This means that, at its simplest level, we can think of a moving coil loudspeaker (at least when it’s not connected to an amplifier...) as an oscillator. Because the friction in the system causes its resonance to decay over time and so we can think of a moving coil loudspeaker as a damped oscillator.
In fact, if you can get your hands on a woofer that isn’t attached to an enclosure, and you hold on to the basket or magnet with one hand, and use your other hand to “thump” the diaphragm or dust cap, you’ll probably hear it ringing at a single note. That note is the loudspeaker driver’s resonant frequency. (If you REALLY want to hear the ringing, connect the speaker terminals to a microphone input on a mixer, and listen to it on a pair of headphones.)
There are a number of ways to find the frequency of that resonance, and how long it will resonate when thumped (in other words, the Q of the resonance) but we’ll deal with that later. For now, it’s just important to understand that this resonance will exist. Also, you should intuitively understand that the greater the mass, the lower the frequency of the resonance. The stiffer the spring (the suspension of the loudspeaker) the higher the frequency of the resonance.
Once upon a time (see Section 2.7), we learned that an inductor (a coil of wire) has an impedance characteristic that, generally speaking, rises with frequency. At DC, the inductor acts just like a wire with an impedance of (nearly) 0 Ω. At ∞ Hz, the inductor has an impedance of ∞ Ω. This characteristic is due to the fact that an AC current causes the magnetic lines of force around the wire in the inductor to move, cutting through adjacent loops in the coil and generating back EMF. At DC, the current isn’t changing, so the magnetic lines of force aren’t moving, so there’s no back EMF being generated.
We have also seen that one of the principal components of a moving coil loudspeaker is the voice coil itself – a coil of wire sitting in a magnetic field. Since it is a coil of wire, it acts as an inductor, although a rather strangely behaving one, due to the fact that it lives and moves in a rather strong magnetic field.
Let’s start by assuming that the voice coil is just an inductor. In this case, it has an impedance curve that we can calculate using Equation 2.92 which stated that XL = 2πfL. Let’s also assume for the purposes of this discussion that the basic inductance of the voice coil is 1 mH (in real life, it will be different for different loudspeakers). A graph the impedance of the voice coil vs. frequency would look like Figure 6.184.
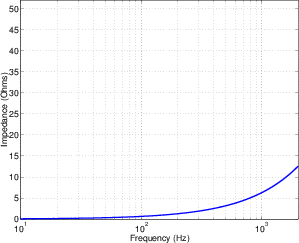
In addition to its basic inductance, the voice coil has a resistance that is frequency-independent. Since it’s independent of frequency (as is the resistance of any resistor...) it can be measured at DC (0 Hz), which is why we call it the DC resistance of the voice coil. That DC resistance is usually low – typically something a little less than 8 Ω. If we just isolate this resistance and add it to the basic inductance of the coil, we would see an impedance curve that looks something like the one shown in Figure 6.185.
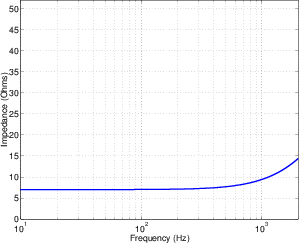
So, even before we attach a diaphragm or a magnet, a loudspeaker coil has the above impedance characteristic. Things get ugly when you add the rest of the loudspeaker to the voice coil. As we saw in the previous section, the driver will have some resonant frequency where a little energy will create a lot of movement because the system is naturally resonating. This causes something very interesting to happen: the loudspeaker starts acting more like a microphone of sorts and produces its own current in the opposite direction to that which you are sending in.
Remember that, for the above graphs, we are looking at the impedance of the coil at different frequencies. When the coil is part of a real speaker, the AC current that we are feeding it causes the coil to move back and forth in the magnetic field of the permanent magnet. When it moves in that field, it generates electricity. When the frequency that you’re playing into it is close to the resonant frequency of the driver, the current that is generated by the coil as it moves in the magnetic field opposes the current that you’re sending to it. Just like the case where the coil is inductive, this opposing current is back EMF and causes some important things:
Figure 6.186 shows an example of the impedance of a voice coil, where the resonance can be seen as a bump in the response. Just above that bump, the impedance drops to an area that is relatively flat for a frequency band before it starts rising again.
The high-frequency behaviour of the voice coil impedance looks a little like an normal inductor, but in fact it’s slightly different. In the case of a real inductor, the impedance rises 6 dB per octave. However, in the case of a loudspeaker driver, there are losses caused by eddy currents in the pole piece, causing the impedance to rise at something more like 3 or 4 dB/oct.
As you add a crossover and more drivers to the system, the impedance curve gets more and more complicated, but we are not going to get into that in this book.
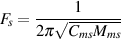 | (6.36) |
where Fs is the resonant frequency of the driver
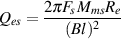 | (6.37) |
where Qes is the electrical Q of the driver at Fs
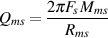 | (6.38) |
where Qms is the mechanical Q of the driver at Fs
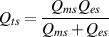 | (6.39) |
where Qts is the total Q of the driver at Fs
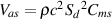 | (6.40) |
where Vas is the volume of air in cubic metres which, when acted upon by a piston of area Sd, has the same compliance as the driver’s suspension. To get Vas in litres, multiply the result of Equation 6.40 below by 1000.
Note that ρ is the density of air (see Section ??) (1.184 kg/m3 at 25∘C), and c is the speed of sound (346.3 m/s at 25∘C).
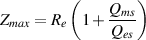 | (6.41) |
where Zmax is the impedance of the loudspeaker at Fs, used when measuring Qes and Qms.
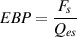 | (6.42) |
where EBP is the Efficiency Bandwidth Product, an indicator of whether a driver should be in a vented or sealed enclosure.
Znom - The nominal impedance of the loudspeaker, typically 4, 8 or 16 Ω.
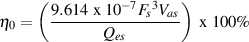 | (6.43) |
where η0 is the reference or ”power available” efficiency of the driver, in percent.
If you’re going to build a loudspeaker, one of the many things you have to consider is the acoustical properties of the system irrespective of the electroacoustical issues. For example, does a loudspeaker that looks like a rectangular box have a different behaviour than one that has smoothed corners, or looks like a sphere? What is the relationship between the radiation of the loudspeaker and the size of the drivers if you’re sitting in the wrong place?
In this chapter, we’ll just deal with a couple of the basic issues that you have to think about if you’re going to build a loudspeaker – or even if you’re just going to complain about someone else’s...
Let’s start with a very simple system. We’ll take two infinitely small loudspeakers and place them a small distance apart from each other as is shown in Figure 6.187. We’ll connect the two loudspeakers to a single sinusoidal signal generator so that they’re producing the same signal at exactly the same time. We saw, once upon a time, way back in Section 3.1.16, that if we’re standing a decent distance away from the loudspeakers, and if we simplify things a little, then what we hear (or what a microphone will measure) is the sum of their pressure outputs. However, that sum must take into account the phase difference of the two loudspeaker signals at the listening position. That phase difference is the result of the two loudspeakers being two different distances from you (unless you’re directly in front of them, of course...)
If you’re in a location where the two loudspeakers are the same distance from you, then the two signals are in phase all the time, and they add together, just as we saw back in Section 3.1.16. This is not very interesting... It’s the same signal, but louder.
So, let’s move to one side a little, so that one of the loudspeakers is closer than the other and think about what happens...
If we produce a low frequency (let’s say that it’s so low that the wavelength is much greater than 2 times the distance between the loudspeakers), then the delay difference caused by the difference in distance to the loudspeakers is small relative to the period of the sinusoid that we’re producing. This, in turn, means that the phase difference between the loudspeakers’ signals at the listening position is close to 0∘, so the signals add together almost as well as if you were standing right in front of them. This is shown in Figure 6.187.
If we now start to increase the frequency of the tone generator, the delay difference between the loudspeakers at the listening position remains constant, but it becomes more and more significant in proportion to the period of the signal (which is getting shorter and shorter as the frequency goes up).
Eventually, we’ll get to a frequency where the wavelength of the sinusoid is two times the difference in the distance to the two loudspeakers when measured from the listening position. For example, if one loudspeaker is 20 cm closer to you than the other, then we’re talking about a sinusoid with a wavelength of 40 cm which corresponds to a frequency of 850 Hz (assuming a speed of sound of 340 m/s).
At this particular frequency, the signals from the two loudspeakers at the listening position will be 180∘ out-of-phase with each other, causing the same effect as if they were opposite in polarity – they cancel each other. In our temporarily perfect world with omnidirectional, infinitely small loudspeakers, and no reflections from other objects, they cancel each other completely, and you hear none of the signal at the listening position. This is illustrated in Figure 6.188.
Note that, as the signal’s frequency went from 0 Hz up to the frequency where it first results in complete cancellation, the phase difference of the two signals at the listening position is moving from 0∘ to 180∘. Consequently, the level at the listening position smoothly drops as you increase the frequency – however, we’ll be more specific about this later.
Now let’s start at the frequency where we get complete cancellation at the listening position and start raising the frequency once more. As before, the delay difference between the loudspeakers’ signals is constant, but it’s increasing in proportion to the period of the signal because the period is getting shorter. Eventually, we’ll get to a frequency where the delay difference is equal to the period of the signal. At this point, the difference in distance to the loudspeakers from the listening position is the same as the wavelength of the signal they are producing. Consequently there is a 360∘ phase difference between the two signals as is illustrated in Figure 6.189. Since we already know that a 360∘ phase shift is identical to a 0∘ phase shift (in other words, no phase shift) then we get complete constructive interference once again, and we hear a sine tone with the same level as our very very low frequency tone that we started with.
In the previous section, we were staying in the same listening position and changing the frequency of the signal sent to the two infinitely small, perfectly omnidirectional loudspeakers to see how the resulting combined signal would behave at one location. Instead of maintaining position and changing the frequency (and ultimately resulting in a frequency response measurement for that position), we could do the opposite – we’ll keep the frequency constant and move our position.
In this case, we’ll maintain a constant distance from a point that is exactly in the middle of the two loudspeakers and rotate around them, changing our angle to the pair, but maintaining a constant distance. Note that we’re keeping a constant distance to the pair, but the individual distances to each driver will change with the angle.
Also, for this section, we’re going to start getting a little more specific about what frequency we’re looking at, and what the spacing between the loudspeakers is. Finally, we’ll assume for this entire section that the speed of sound in air is 340 m/s, which is close enough – it might even be true, depending on the temperature.
10 Hz
Let’s put the loudspeakers 34 cm apart and set the frequency of the tone generator to 10 Hz. The wavelength of a 10 Hz sinusoid is 34 m which 100 times longer than the spacing between our loudspeakers. In a best-case scenario, when you’re the same distance from two drivers, the phase difference at the listening position will be 0∘. Let’s call the output that you measure at that location our reference level, so, on a linear scale, we’ll arbitrarily say that this is a value of 1, which we’ll call our reference value of 0 dB. The actual level isn’t so exciting, since it’s affected by the power output of the loudspeakers and your distance to them. What’s more interesting for us right now is how the level changes when your position changes, so we’ll just compare the level at other locations to the one at the front.
In a worst-case situation, you are standing 90∘ off-axis to the pair – in other words, you are to one side of the loudspeaker array, so the difference in distance is as big as it can be. In this case, the difference in distance between the speakers is 1/100th of the wavelength of the sinusoid, which means that the phase difference at the listening position will be 1/100th of 360∘, or 3.6∘. Since this phase difference is so small, you’ll get almost no loss of signal to the side of the loudspeaker array compared to directly in front of it.
If we calculate the combined output for the two loudspeakers for all angles in front of the pair, we can plot the resulting level (since they’re omnidirectional, the back of the pair will be symmetrical to the front, so plotting it is redundant). This is shown in Figure 6.190.
Figure 6.190 shows the output, plotted on a linear and a decibel scale, on a cartesian plot. This is useful, but a more intuitive representation is a polar plot which shows the angle to the loudspeaker pair as an angle on the plot rather than as the X-axis. This polar plot can show the level on a linear scale, as is shown in Figure 6.191 or on a decibel scale as in Figure 6.192.
At this point, you may be wondering why I’m plotting the same data on cartesian and polar plots, both in linear and decibel scales. At the moment, I’ll admit that there’s no good reason, but there will be later in the section.
250 Hz
Let’s now increase the frequency of the tone generator to 250 Hz, keeping the loudspeakers in the same locations, and keeping your distance to the pair. In this particular situation the wavelength of the tone is 4 times the separation of the loudspeaker drivers, so if we move our listening position from 0∘ (in front) to 90∘ (to one side) of the loudspeaker array, we’ll be changing smoothly from perfect constructive interference to a level equivalent to what we would have gotten if only one of the loudspeakers was playing.4
If we plot the resulting output vs. angle of the listening position relative to the loudspeaker pair for 250 Hz, we’ll get responses as are shown in Figures 6.193, 6.194 and 6.195.
Note in these plots that the signal drops from 0 dB at the front of the pair to -6 dB at the side of the pair.
500 Hz
If we repeat the same measurements at 500 Hz, we’ll now see that as we approach the side of the loudspeaker pair, the combined output at the listening position goes to 0, or -∞ dB. This is because the 34 cm distance between the loudspeakers is equal to one half the wavelength of 500 Hz. So, at the listening position, the signals are 180∘ out-of-phase, so they cancel each other completely.
If we look at the representation of the pattern on a linear polar scale, we can see that the radiation of the loudspeaker array has what is called a lobe. This is a teardrop-shaped area on a polar plot that tells us there is a range of angles relative to the loudspeaker pair where the combined signal is higher than in other places.
When the polar plot is shown on a decibel scale, the lobe appears to be much wider. This is because a decibel scale gives us a better representation of lower-level signals, so it appears to emphasise the quieter areas of the lobe. In fact, although many books will show the radiation pattern of a loudspeaker on a polar plot with a linear scale as in 6.197, it makes more sense to us humans to look at the decibel version as is shown in Figure 6.198. (However, I’ll talk later about cases where this is not true.)
1000 Hz
When the signal has a frequency of 1 kHz, its wavelength is the same as the distance between the loudspeakers. Consequently, we’ll get a cancellation at 30∘ off-axis to the pair, and we’ll get complete constructive interference at 90∘. This is shown in Figures 6.199, 6.200 and 6.201.
You can see in Figures 6.200 and 6.201 that, if we’re only thinking about the “front” of the loudspeaker pair, there are three lobes where we get a maximum output from the array. In fact, since the back side of our pair of omnidirectional loudspeakers is symmetrical to the front, at 1 kHz, we actually have 4 lobes in a cloverleaf-shaped pattern.
2000 Hz
If the frequency of the tone is increased, we’ll see more and more lobes appearing. To illustrate this, we’ll look at two more frequencies. Figures 6.202, 6.203 and 6.204 show the radiation pattern of the loudspeaker pair for 2 kHz. As you can see, this results in 5 lobes in front of the pair.
10000 Hz
At 10 kHz, the wavelength is very small compared with the separation between the loudspeakers, so we get a large number of lobes in front of our loudspeaker pair as can be seen in Figures 6.205, 6.206 and 6.207.
Let’s set the frequency of the signal generator to 5 kHz. We’ll leave the separation of our infinitely small, omnidirectional loudspeakers at 34 cm and do the same measurement of the output level relative to angle to the listening position the linear-scale polar representation of the radiation pattern of this array is shown in Figure 6.208.
Now we’ll add an extra loudspeaker at the exact midpoint between them. So, now we have three loudspeakers all connected in parallel to the tone generator, and we’ll repeat our measurement.
Let’s start by looking at the cartesian representation of the result as is shown in Figure 6.209.
There are three important things to notice in this plot.
The first, and most obvious, is the change in the relative levels of the lobes. In Figure 6.209 (with only 2 loudspeakers) we saw that there are 11 lobes, all with the same maximum level. In Figure 6.210 (3 loudspeakers) we have the same number of lobes, but 6 of them (every alternate one) have a lower level.
The second is a question of cancellation. In the case of two loudspeakers, in between each lobe, there is complete cancellation. On a linear cartesian plot, this means that the dip between each bump bottoms out at a value of 0. On a dB scale, it means that the troughs are deep notches that drop to -∞. In the case of 3 loudspeakers, things are a little more complicated as can be seen in the dB scale plot in Figure 6.209.
Finally, there is the question of polarity. In the case of two loudspeakers, all of our linear values ranged between 0 and 1, inclusive. However, now that we’ve added an extra loudspeaker, if you look carefully, you’ll see that our dips in the response on the linear scale drop below 0. This means that, at some specific angles, the signal will be opposite in polarity to other angles. It’s counterintuitive to represent this on a polar plot because it will look like the lobe is pointing in the wrong direction. (This is because a negative value at 0∘ is plotted like a positive value at 180∘. Negative values at 45∘ look like positive ones at 225∘, and so on.)
If we increase the number to 4, equally spaced loudspeakers, with the most distant ones staying at 34 cm, we’ll see another change in the overall radiation pattern of the combined output at different angles. I’ll just plot the theoretical response here without discussing it.
One thing worth mentioning here before things get more difficult to see is that the angles of the maximum points of each lobe aren’t changing as we add more loudspeakers – This is determined by the separation between the two outside loudspeakers. The only things that are really changing are the individual amplitudes of the lobes.
Let’s now increase to 8 drivers. Now we can see in Figures 6.215, 6.216, and 6.217 we now have one principal lobe that beams at an angle of 0∘. All other lobes are much lower in level.
If we double the number of loudspeakers again, to a total of 16, we’ll see that the difference between the main lobe and all of the others becomes greater as is shown in Figures 6.218, 6.219, and 6.220.
Let’s go crazy. We’ll put a very large number of loudspeakers – 256, equally spaced units in a straight line, with the outside ones still 24 cm apart. (In other words, we have less than 1 mm between each loudspeaker.) If we plot the theoretical radiation pattern of this array, we’ll see that there is basically just one main beam at 5 kHz as is shown in Figures 6.221, 6.222, and 6.223.
Up to now, we’ve been looking at a weird sort of thing... a collection of infinitely-small, omnidirectional loudspeakers, sitting in a row. This, of course, doesn’t exist in real life, however, it’s a good way to think of all the molecules sitting next to each other on the face of a loudspeaker.
That which we call a “loudspeaker driver” in real life is usually more like a cone with a bump at the bottom, as we saw an earlier section. Let’s simplify that shape and pretend that it’s just a flat circle that moves in and out its cabinet. We’ll also simplify the border between the driver and the cabinet it sits in and say that there is no connection between the two, but there’s no leak either. Also, we’ll pretend that the face of the speaker cabinet is infinitely big. So, we have a wall that extends to infinity in all directions (what loudspeaker engineers call a “2 π baffle” (say “two-pi baffle”)), and there’s a hole in that wall with a circular piston that moves in and out.
Let’s pretend that we did have such a thing and we took a look at its directivity. As we’ve already seen with the array of drivers, we’d expect our “speaker” (actually, a piston) to be omnidirectional at low frequencies and increasingly directional as we go up in frequency. It probably won’t come as a surprise to find out that this is exactly what happens. Figures 6.224 and 6.225 show the output of a piston with a diameter of 34 cm at frequencies ranging from 10 Hz to 10 kHz, with an angular range of ±90∘. You can see there that we get an omnidirectional response at low frequencies, and a very narrow beam off the front of the piston at high frequencies. The frequency area where we transition from omni to directional is around the frequency that has a wavelength equal to the diameter of the piston – 1 kHz (plus/minus an octave... it’s a wide transition band...).
You can also see in Figure 6.224, just like in the case of the array, that, at some angles at higher frequencies, the signal is opposite in polarity from the main on-axis beam.
If we plot the same information in decibels, we get the graphs in Figures 6.226 and 6.227. Notice that, at 10 kHz, we’re more than 20 dB down from the level on-axis, at less than 10∘ off-axis. This means, in real life, that if you move just a little bit out of that beam, all of your high-end will seem to completely disappear...
Let’s consider this in a different way. All of the plots in this section so far show you what happens if you play a frequency, and then move out of the direct line of fire. What’s more likely is that you’re listening to more than one frequency – music, for example, and sitting somewhere off-axis. So, let’s look at the frequency response of the piston at different angles. This is shown in Figures 6.228, 6.229 and 6.230. You should see in these plots that, as you sit further off-axis to the loudspeaker (i.e. the more to the side) the lower the high-frequency cutoff of the signal.
Okay, so by now, you’re probably sitting there thinking “this is lovely, but he’s only talking about theoretical things like infinitely small speakers or flat-faced pistons... what about real loudspeakers?” Well... I have some very bad news... I’m not going to talk about real loudspeakers. The reason for this glaring omission is that the actual shape of a loudspeaker driver has a huge effect on the details of directional characteristics, but without getting into some very serious math that goes way over my head, we won’t get anywhere. So, this is as close as I’m going to get to the Truth. If you want to come closer, then you’ll just have to go looking somewhere else... (John Eargle’s Loudspeaker Handbook is a good choice) Sorry.
There are a number of reasons why you should care about this.
The simplest reason is knowing the relationship between the diameter of a loudspeaker, its frequency range, and the resulting range of movement you have. If you have a 34 cm diameter woofer that is running up to 10 kHz (this is silly...) then you have to be in the on-axis beam, or you won’t hear any high end.
START WRITING HERE!!
- Enclosure Design (i.e. “what does the box look like?”) of which there are a number of possibilities including the following:
- Dipole Radiator (no enclosure) - Infinite Baffle - Finite Baffle - Folded Baffle - Sealed Cabinet (aka Acoustic Suspension) - Ported Cabinet (aka Bass Reflex)
- Horns (aka Compression Driver)
(no enclosure)
aka a Doublet Radiator
Since both sides of a dipole radiator’s diaphragm are exposed to the outside world (better known as your listening room) there are opposite polarity pressures being generated in the same space (albeit at different locations) simultaneously. As the diaphragm moves “outwards” (i.e. towards the listener), the resulting air pressure at the “front” of the diaphragm is positive while the pressure at the back of the diaphragm is of equal magnitude but opposite polarity.
At high frequencies, the diaphragm beams (meaning that it’s directional – it only sends the energy out in a narrow beam rather than dispersing it in all directions) as if the rear side of the diaphragm were sealed. The result of this is that the negative pressure generated by the rear of the diaphragm does not reach the listener. For more information on beaming see section 1.6 of the Loudspeaker and Headphone Handbook edited by John Borwick and published by Butterworth.
At low frequencies, the delay time required for energy to travel from the back of the diaphragm to the front and towards the listener is a negligible part of the phase of the wave (i.e. the distance around the diaphragm is very small compared to the wavelength of the frequency). Since the energy at the rear of the diaphragm is opposite in polarity to the front, the two cancel each other out at the listening position.
The result of all this is that a dipole radiator doesn’t have a very good low frequency response – in fact, it acts much like a high pass filter with a slope of 6 dB/octave and a cutoff frequency which is dependent on the physical dimensions of the diaphragm.
How do we fix this?
The biggest problem with a dipole radiator is caused by the fact that the energy from the rear of the diaphragm reaches the listener at the front of the diaphragm. The simplest solution to this issue is to seal the back of the diaphragm as shown.
This is called an “infinite baffle” because the diaphragm is essentially mounted on a wall of infinite dimensions. (Another way to draw this would have been to put the diaphragm mounted in a small hole in a wall that goes out forever. The problem with that kind of drawing is that my stick man wouldn’t have had anything to stand on.)
Disadvantages
- You’re automatically throwing away half of your energy (the half that’s radiated by the rear of the diaphragm
- Costs... How do you build a wall of infinite dimensions?
Advantages
- Lower low-frequency cutoff than a dipole radiator.
Now the low cutoff frequency is dependent on the diameter of the diaphragm according to the following equation:
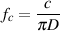 | (6.44) |
Where fc is the low frequency cutoff in Hz (-3 dB point)
c is the speed of sound in air in m/s
D is the diameter of the loudspeaker in m
Unlike the dipole radiator, frequencies below the cutoff have a pressure response of 12 dB/octave (instead of 6 dB/octave). Therefore, if we’re going down in frequency comparing a dipole radiator and an infinite baffle with identical diaphragms, the infinite baffle will go lower, but drops off more quickly past that frequency.
Instead of trying to build a baffle with infinite dimensions, what would happen if we mounted the diaphragm on a circular baffle of finite dimensions as shown below?
Now, the circular baffle causes the energy from the rear of the driver to reach the listener with a given delay time determined by the dimensions of the baffle. This causes a comb-filtering effect with the first notch happening where the path length from the rear of the driver to the front of the baffle equals one wavelength as shown below:
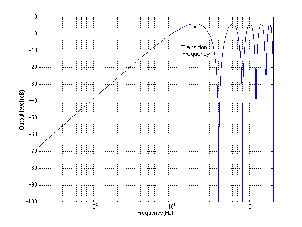
One solution to this problem is to create multiple path lengths by using an irregularly-shaped baffle. This causes multiple delay times for the pressure from the rear of the diaphragm to reach the front of the baffle. The technique will eliminate the comb filtering effect (no notches above the transition frequency) but we still have a 6 dB/octave slope in the low end (below the transition frequency). If the baffle is very big (approaching infinite relative to the wavelength of the lowest frequencies) then the slop in the low end approaches 12 dB/octave – essentially, we have the same effect as if it were an infinite baffle.
If the resonant frequency of the driver, below which the roll-off occurs at a slope of 6 dB/octave, is the same as (or close to) the transition frequency of the baffle, the slope becomes 12 or 18 dB/octave (dependent on the size of the baffle – the slopes add). The resonant frequency of the driver is the rate at which the driver would oscillate if your thumped it with your finger – though we’ll talk about that a little more in the section on impedance.
What do you do if you don’t have enough room in your home for big baffles? You fold them up!
(aka Open-back Cabinet)
A folded baffle is essentially a large flat baffle that has been “folded” into a tube which is open on one end (the back) and sealed by the driver at the other end as is shown below.
The fact that there’s a half-open tube in the picture causes a nasty resonance (see the section on resonance in the Acoustics section of this textbook for more info on why this happens) at a frequency determined by the length of the tube.
wavelength of the resonant frequency = 4 * length of the tube
The low frequency response of this system is the same as in the case of finite baffles.
(aka Acoustic Suspension)
We can eliminate the resonance of an open-back cabinet by sealing it up, thus turning the tube into a box.
Now the air sealed inside the enclosure acts as a spring which pushes back against the rear of the diaphragm. This has a number of subsequent effects:
- increased resonant frequency of the driver
- reduced efficiency of the driver (because it has to push and pull the “spring” in addition to the air in the room)
- non-symmetrical distortion (because pushing in on the “spring” has a different response than pulling out on it)
We’re throwing away a lot of energy as in the case of the infinite baffle because the back of the driver is sealed off to the world.
Usually the enclosure has an acoustic resonant frequency (sort of like little room modes) which is lower than the (now raised...) resonant frequency of the driver. This effectively lowers the low cutoff frequency of the entire system, below which the slope is typically 12 dB/octave.
(aka Bass Reflex)
You can achieve a lower low cutoff frequency in a sealed cabinet if you cut a hole in it – the location is up to you (although, obviously, different locations will have different effects...)
If you match the cabinet resonance, which is determined by the volume of the cabinet and the diameter and length of the hole (look up Helmholtz resonators in the Acoustics section), with the speaker driver resonance properly (NOTE: Could someone explain to me what a “properly matched” cabinet and driver resonance means?), you can get a lower low frequency cutoff than a sealed cabinet, but the low frequencies now roll off at a slope of 24 dB/octave.
(aka Compression Drivers)
The efficiency of a system in transferring power is determined by how the power delivered to the system relates to the power received in the room. For example, if I were to send a signal to a resistor from a function generator with an output impedance of 50Ω, I would get the most power dissipation in the resistor if it had a value of 50Ω. Any other value would mean that less power would be dissipated by the device. This is because its impedance would be matched to the internal impedance of the function generator.
Consider loudspeakers to have the same problem: the transfer motion (kinetic energy, if you’re a geek) or power from a moving diaphragm to the air surrounding it. The problem is that the air has much lower acoustic impedance than the driver (meaning, it’s easier to move back and forth), therefore our system isn’t very efficient.
Just as we could use a transformer to match electrical impedances in a circuit (providing a Req rather than the actual R) we can use something called a horn to match the acoustic impedances between a driver and the air.
There are a couple of things to point out regarding this approach:
- The diaphragm is mounted in a small chamber which opens to the horn
- At point “a” (the small area of the horn) there is a small area of air undergoing a large excursion. The purpose of the horn is to slowly change this into the energy at point “b” where we have a large area with a small excursion. In other words, the horn acts as an impedance matching device, ensuring that we have an optimal power transfer from the diaphragm to the air in the room.
- Notice that the diaphragm is large relative to the opening to the horn. This means that, if the diaphragm moves as a single unit (which it effectively does) there is a phase difference (caused by propagation delay differences to the horn) between the pressure caused by the centre of the diaphragm and the pressure caused by the edge of the diaphragm. Luckily, this problem can be avoided with the insertion of a plug which ensures that the path lengths from different parts of the diaphragm to the centre of the throat fo the horn are all equal.
In the above diagram, the large black area is the cross section of the plug with hole drilled in it (the white lines). Each hole is the same length, ensuring that there is no interference, either constructive or destructive, caused by multiple path lengths from the diaphragm to the horn.
As a general rule of thumb, a loudspeaker is almost completely omnidirectional (it radiates energy spherically – in all directions) when the driver is equal to or less than 1/4 the wavelength of the frequency being produced. The higher the frequency, the more directional the driver.
Why is this a problem?
High frequencies are very directional, therefore if your ear is not in the direct “line of fire” of the speaker (that is to say, “on axis”) then you are getting some high-frequency roll-off.
In the case of low frequencies, the loudspeaker is omnidirectional, therefore you are getting energy radiating behind and to the sides of the speaker. If there’s a nearby wall, floor or ceiling, the pressure which bounces off it will add to that which is radiating forward and you’ll get a boost in the low end.
- If you’re near 1 surface, you get 3 dB more power in the low end
- If you’re near 2 surfaces, you get 6 dB more power in the low end
- If you’re near 3 surfaces, you get 9 dB more power in the low end
The moral of this story? Unless you want more low end, don’t put your loudspeaker in the corner of the room.
We said much earlier that drivers are usually optimized for specific frequency bands. Therefore, an easy way to get a wide-band loudspeaker is to use multiple drivers to cover the entire audio range. Most commonly seen these days are 2-way loudspeakers (meaning 2 drivers, usually in 1 enclosure), although there are many variations on this.
If you’re going to use multiple drivers, then you have some issues to contend with:
1 – Crossovers
- You don’t want to send high frequencies to a low frequency driver (aka woofer or low frequencies to a high-frequency driver (aka tweeter). In order to avoid this, you filter the signals getting sent to each driver – the woofer’s signal is routed through a low-pass filter, while the tweeter’s is filtered using a high-pass. If you are using mid-range drivers as well, then you use a band-pass filter for the signal. This combination of filters is known as a crossover.
Most filters in crossovers have slopes of 12 or 18 dB/octave (although it’s not uncommon to see steeper slopes) and have very specific designs to minimize phase distortion around the crossover frequencies (the frequencies where the two filters overlap and therefore the two drivers are producing roughly equal energy) This is particularly important because crossover frequencies are frequently (sorry... I couldn’t resist at least one pun) around the 1 – 3 kHz range – the most sensitive band of our hearing.
There are two basic types of crossovers, active and passive.
These are probably what you have in your home. Your power amplifier sends a full-bandwidth signal to the crossover in the loudspeaker enclosure which, in turn, sends filtered signals to the various drivers. This system has a drawback in that it wastes power from your amplifier – anything that is filtered out is lost power. “Audiophiles” (translation: “people with too much disposable income who spend more time reading reviews of their audio equipment than they do actually listening to it”) also complain about issues like back EMF and cabinet vibrations which may or may not affect the crossover. (I’ll believe this when I see some data on it...). The advantage of passive crossovers is that they’re idiot-proof. You plug in one amplifier to one speaker input and the system works and works well. Also – they’re inexpensive.
These are filters that precede the power amplifier in the audio chain (the amplifier is then directly connected to the individual driver). They are more efficient, since you only amplify the required frequency band for each driver – then again, they’re more expensive because you have to buy the crossover plus extra amplifiers.
2 – Crossover Distortion
There is a band of frequencies around the cutoffs of the crossover filters where the drivers overlap. At this point you have roughly equal energy being emitted by at least two diaphragms. There is an acoustic interaction between these two which must be considered, particularly because it is in the middle of the audio range usually.
In order to minimize problems in this band, the drivers must have matched distances to the listener, otherwise, you’ll get comb filtering due to propagation delay differences. This so-called time aligning can be done in one of two ways. You can either build the enclosure such that the tweeter is set back into the face of the cabinet, so its voice coil is vertically aligned with the voice coil of the deeper woofer. Or, alternately you can use an electronic delay to retard the arrival of the signal at the closer driver by an appropriate amount.
3 – Interaction between drivers
Remember that the air inside the enclosure acts like a spring which pushes and pulls the drivers contrary to the direction you want them to move in. Imagine a woofer moving into a cabinet. This increases the air pressure inside the enclosure which pushes out against both the woofer AND the tweeter. This is bad thing. Some manufacturers get around this problem by putting divided sections inside the cabinet – others simply build separate cabinets – one for each driver (as in the B and W 801).
Until I get something written on this topic, I would highly recommend that you just read anything you can by Wolfgang Klippel. His tutorials on loudspeaker nonlinearities are available from the Audio Engineering Society and his own website.