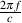This list, shown in Table 12.1 is a standard list of frequencies that can be used for various
things such as the centre frequencies for graphic equalizers. The numbers are used a
multipliers for the decades within the audio range. For example, if you were building an
equalizer with two-third-octave frequency centres, the filters would have centre
frequencies of 25 Hz, 40 Hz, 63 Hz, 100 Hz, 160 Hz, 250 Hz, 400 Hz, 630
Hz, 1000 Hz, 1600 Hz, 2500 Hz, 4000 Hz, 6300 Hz, 10000 Hz, and 16000
Hz.
Use the numbers listed in the table as multipliers. For example, if you were building
a one-octave equalizer, then its frequency centres would use the right-most column of
numbers. In Hz, these would be 10 Hz, 20 Hz, 40 Hz, 80 Hz, 100 Hz, 200 Hz, 400 Hz,
800 Hz, 1 kHz, 2 kHz, 4 kHz, 8 kHz, 10 kHz, 20 kHz and so on. If you’re really paying
attention here, you’ll notice that these aren’t really octave divisions... because 1 kHz is
not one octave above 800 Hz.
If you go to the resistor store, you can buy different types of resistors in different
sizes. Some fancy types will have the resistance stamped right on them, but
most just have bands of different colours around them as is shown in Figure
12.1.
The bands are used to indicate a couple of pieces of information about the resistor.
In particular, you can find out both the resistance of the device, as well as its
tolerance.
Firstly, let’s talk about what the tolerance of a resistor is. Unfortunately, it’s
practically impossible to make a resistor that has exactly the resistance that
you’re looking for in your circuit. Instead of guaranteeing a particular value
such as 1 kΩ, the manufacturer tells you that the resistance is approximately 1
kΩ, ± some percentage. For example, you’ll see something like 1 kΩ, ±20%.
Therefore, if you measure the resistor, you’ll see that it has a value between 800
Ω and 1.2 kΩ. If you want better precision than that, you’ll have to do one
of two things. You’ll either have to spend more money to get resistors with a
tighter tolerance, or you’ll have to hand-pick them yourself by measuring one by
one.
So, how do we tell what the specifications of a resistor are just by looking at it? Take
a look at Figure 12.2. You’ll see that each band has a label attached to it. Reading from
left to right (the right side of the resistor doesn’t have a colour band) we have the 1st and
2nd digits, the multiplier and the tolerance. Using Table 12.2 we can figure out what the
shown resistor is.
|
|
|
|
|
| Colour | Digit | Multiplier | Carbon ± | Film-type |
| | | | Tolerance | Tolerance |
|
|
|
|
|
| Black | 0 | 1 | 20% | 0 |
| Brown | 1 | 10 | 1% | 1% |
| Red | 2 | 100 | 2% | 2% |
| Orange | 3 | 1,000 | 3% | |
| Yellow | 4 | 10,000 | GMV | |
| Green | 5 | 100,000 | 5% (alt) | 0.5% |
| Blue | 6 | 1,000,000 | 6% | 0.25% |
| Violet | 7 | 10,000,000 | 12.5% | 0.1% |
| Gray | 8 | 0.01 (alt) | 30% | 0.05% |
| White | 9 | 0.1 (alt) | 10% (alt) | |
| Silver | | 0.01 (pref) | 10% (pref) | 10% |
| Gold | | 0.1 (pref) | 5% (pref) | 5% |
| No colour | | | 20% | |
|
|
|
|
|
| |
Table 12.2: The corresponding meanings of the colour bands on a resistor [Mandl,
1973]. (GMV stands for Guaranteed minimum value
The colour bands on the resistor in Figure 12.2 are red, green, violet and silver. Table
12.3 shows how this combination is translated into a value.
|
|
|
|
| 1st digit | 2nd digit | Multiplier | Tolerance |
|
|
|
|
| red | green | violet | silver |
| 2 | 5 | 10,000,000 | 10% |
|
|
|
|
| |
Table 12.3: Using Table 12.2, the colour bands can be used to find that the resistor
in Figure 12.1 has a value of 250,000,000 Ω or 250 MΩ, ±10%.
|
|
|
| Letter | small | Capital |
|
|
|
| Alpha | α | A |
| Beta | β | B |
| Gamma | γ | Γ |
| Delta | δ | Δ |
| Epsilon | ϵ | E |
| Zeta | ζ | Z |
| Eta | η | H |
| Theta | θ | Θ |
| Iota | ι | I |
| Kappa | κ | K |
| Lambda | λ | Λ |
| Mu | μ | M |
| Nu | ν | N |
| Xi | ξ | Ξ |
| Omicron | o | O |
| Pi | π | Π |
| Rho | ρ | P |
| Sigma | σ | Σ |
| Tau | τ | T |
| Upsilon | υ | Υ |
| Phi | ϕ or φ | Φ |
| Chi | χ | X |
| Psi | ψ | Ψ |
| Omega | ω | Ω |
|
|
|
| |
Table 12.4: Greek letters
There are a number of letters that have common usage that make them sort of
unavailable for other uses. I’ve put the really typically used ones below in alphabetical
order.
Δ – the difference between two things
λ - wavelength
μ – micro, or * 10-6
π – the constant Pi, or, truncated to 50 places after the decimal,
3.141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 10
Σ – the addition of
τ – time constant. See Section [].
ω – radian frequency. 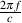
Ω – Ohms, a unit of impedance, either electrical, acoustical or mechanical.
 Oct
Oct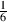 Oct
Oct Oct
Oct Oct
Oct Oct
Oct