
One of my first professors in Digital Signal Processing (better known as DSP) summarized the entire field using the simple flowchart shown in Figure 9.1.

Essentially, that’s just about it. The idea is that you have some signal that you have converted from analog to a discrete representation using the procedure we saw in Section 8.1. You want to change this signal somehow – this could mean just about anything... you might want to delay it, filter it, mix it with another signal, compress it, make reverberation out of it – anything... Everything that you want to do to that signal means that you are going to take a long string of numbers and turn them into a long string of different numbers. This is processing of the digital signal or, Digital Signal Processing – it’s the math that is applied to the signal to turn it into the other signal that you’re looking for.
Usually, a block diagram of a DSP algorithm won’t run from top to bottom as is shown in Figure 9.1. Just like analog circuit diagrams, DSP diagrams typically run from left to right, with other directions being used either when necessary (to make a feedback loop, for example) or for different signals like control signals as in the case of analog VCA’s (See section 6.2.3).
Let’s start by looking at a block diagram of a simple DSP algorithm.
Let’s look at all of the components of Figure 9.2 to see what they mean.
Looking from left to right you can see the following:
There is another way of expressing this block diagram using math. Equation 9.1 shows exactly the same information without doing any drawing.
![y[t]= x[t]+ ax[t- k]](intro_to_sound_recording770x.png) | (9.1) |
If you start reading books about DSP, you’ll notice that they use a strange way of labeling the frequency of a signal. Instead of seeing graphs with frequency ranges of 20 Hz to 20 kHz, you’ll usually see something called a normalized frequency ranging from 0 to 0.5 and no unit attached (it’s not 0 to 0.5 Hz).
What does this mean? Well, think about a digital audio signal. If we record a signal with a 48 kHz sample rate and play it back with a 48 kHz sampling rate, then the frequency of the signal that went in is the same as the frequency of the signal that comes out. However, if we play back the signal with a 24 kHz sampling rate instead, then the frequency of the signal that comes out will be one half that of the recorded signal. The ratio of the input frequency to the output frequency of the signal is the same as the ratio of the recording sampling rate to the playback sampling rate. This probably doesn’t come as a surprise. (Remember as well that since a change in sampling rate will change the sampling period – the time it takes to play one sample – then a delay composed of an integer number of samples will also change its length in time.)
What happens if you really don’t know the sampling rate? You just have a bunch of samples that represent a time-varying signal. You know that the sampling rate is constant, you just don’t know its frequency. This is the what a DSP processor “knows.” So, all you know is what the frequency of the signal is relative to the sampling rate. If the samples all have the same value, then the signal must have a frequency of 0 (the DSP assumes that you’ve done your anti-aliasing properly...). If the signal bounces back between positive and negative on every sample, then its frequency must be the Nyquist Frequency – one half of the sampling rate.
So, according to the DSP processor, the sampling rate has a frequency of “1” and your signal will have a frequency that can range from 0 to 0.5. This is called the normalized frequency of the signal.
There’s an important thing to remember here. Usually people use the word “normalize” to mean that something is changed (you normalize a mixing console by returning all the knobs to a default setting, for example). With normalized frequency, nothing is changed – it’s just a way of describing the frequency of the signal.
PUT A SHORT DISCUSSION HERE REGARDING THE USE OF ωt
NOTE TO SELF: CHECK ALL THE COMPLEX NUMBERS IN THIS SECTION
If you’re unhappy with the concepts of real and imaginary components in a signal, and how they’re represented using complex numbers, you’d better go back and read Chapter 1.6.
We saw briefly in Section 3.1.17 that there is a direct relationship between the time and frequency domains for a given signal. In face, if we know everything there is to know about the frequency domain, we already know its shape in the time domain and vice versa. Now let’s look at that relationship a little more closely.
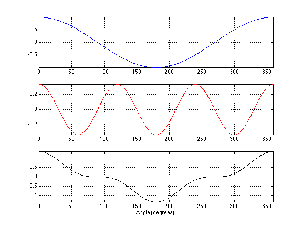
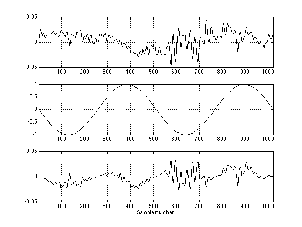
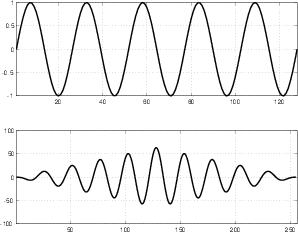
Take a sine wave like the top plot shown in Figure 9.3 and add it to another sine wave with one third the amplitude and three times the frequency (the middle plot, also in Figure 9.3). The result will be shaped like the bottom plot in Figure 9.3.
If we continue with this series, adding a sine wave at 5 times the frequency and 1/5th the amplitude, 7 times the frequency and 1/7th the amplitude and so on up to 31 times the frequency (and 1/31 the amplitude) you get a waveform that looks like Figure 9.4.

As is beginning to become apparent, the result starts to approach a square wave. In fact, if we kept going with the series up to ∞ Hz, the sum would be a perfect square wave.
The other issue to consider is the relative phase of the harmonics. For example, if we take the same sinusoids as are shown in Figures 9.3 and 9.4 and offset each by 90∘ before summing, we get a very different result as can be seen in Figures 9.5 and 9.6.
This isn’t a new idea – in fact, it was originally suggested by a guy named Jean Baptiste Fourier that any waveform (such as a square wave) can be considered as a sum of a number of sinusoidal waves with different frequencies and phase relationships. This means that we can create a waveform out of sinusoidal waves like we did in Figures 9.3 and 9.4, but it also means that we can take any waveform and look at its individual components. This concept will come as no surprise to musicians, who call these components “harmonics” – the timbres of a violin and a viola playing the same note are different because of the different relationships of the harmonics in their spectra (one spectrum, two spectra)
Using a lot of math – and calculus, it is possible to calculate what is known as a Fourier Transform of a signal to find out what its sinusoidal components are. We won’t do that. There is also a way to do this quickly – called a Fast Fourier Transform or FFT. We won’t do that either. The FFT is used for signals that are continuous in time. As we already know, this is not the case for digital audio signals, where time and amplitude are divided into discrete divisions. Consequently, in digital audio we use a variation on the FFT called a Discrete Fourier Transform or DFT. This is what we’ll look at. One thing to note is that most people in the digital world use the term FFT when they really mean DFT – in fact, you’ll rarely hear someone talk about DFT’s – even through that’s what they’re doing. Just remember, if you’re doing what you think is an FFT to a digital signal, you’re really doing a DFT.
Let’s take a digital audio signal and view just a portion of it, shown in Figure 9.7. We’ll call that portion the window because the audio signal extends on both sides of it and it’s as if we’re looking at a portion of it through a window. For the purposes of this discussion, the window length, usually expressed in points is only 1024 samples long (therefore, in this case we have a 1024-point window).
As we already know, this signal is actually a string of numbers, one for each sample. To find the amount of 0 Hz in this signal, all we need to do is to add the values of all the individual samples. Technically speaking, we really should make it an average and divide the result by the number of samples, but we’re in a rush, so don’t bother. If the wave is perfectly symmetrical around the 0 line (like a sinusoidal wave, for instance...) then the total will be 0 because all of the positive values will cancel out all of the negative values. If there’s a DC component in the signal, then adding the values of all the samples will show us this total level.
So, if we add up all the values of each of the 1024 samples in the signal shown, we get the number 4.4308. This is a measure of the level of the 0 Hz component (in electrical engineering jargon, the DC offset) in the signal. Therefore, we can say that the bin representing the 0 Hz component has a value of 4.4308. Note that the particular value is going to depend on your signal, but I’m giving numbers like “4.4308” just as an example.
We know that the window length of the audio signal is, in our case, 1024 samples long. Let’s create a cosine wave that’s the same length, counting from 0 to 2π (or, in other words, 0 to 360∘). (Technically speaking, its period is 1025 samples, and we’re cutting off the last one...) Now, take the signal and, sample by sample, multiply it by its corresponding sample in the cosine wave as shown in Figure 9.8.

Now, take the list of numbers that you’ve just created and add them all together (for
this particular example, the result happens to be 6.8949). This is the “real” component at
a frequency whose period is the length of the audio window. (In our case, the window
length is 1024 samples, so the period for this component is 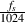 where fs is the sampling
rate.)
where fs is the sampling
rate.)
Repeat the process, but use a sine wave instead of a cosine and you get the imaginary component for the same frequency, shown in Figure 9.9.

Take that list of numbers and add them and the result is the “imaginary” component at a frequency whose period is the length of the sample (for this particular example, the result happens to be 0.9981).
Let’s assume that the sampling rate is 44.1 kHz, this means that our bin representing the frequency of 43.0664 Hz (remember, 44100/1024) contains the complex value 6.8949 + 0.9981i. We’ll see what we can do with this in a moment.
Now, repeat the same procedure using the next harmonic of the cosine wave, shown in Figure 9.10.
Take that list of numbers and add them and the result is the “real” component at a frequency whose period is the one half the length of the audio window (for this particular example, the result happens to be -4.1572).
And again, we repeat the procedure with the next harmonic of the sine wave, shown in Figure 9.11.
Take that list of numbers and add them and the result is the “imaginary” component at a frequency whose period is the length of the sample (for this particular example, the result happens to be -1.0118).
If you want to calculate the frequency of this bin, it’s 2 times the frequency of the
last bin (because the frequency of the cosine and sine waves are two times the
fundamental). Therefore it’s 2 , or, in this example, 2 * (44100/1024) = 86.1328
Hz.
, or, in this example, 2 * (44100/1024) = 86.1328
Hz.
Now we have the 86.1328 Hz bin containing the complex number -4.1572 – 1.0118i.
This procedure is repeated, using each harmonic of the cosine and sine until you get up to a frequency where you have 1024 periods of the cosine and sine in the window. (Actually, you just go up to the frequency where the number of periods in the cosine or the sine is equal to the length of the window in samples.)
Using these numbers, we can create Table 9.1.
| Bin | Frequency (Hz) | Real | Imaginary |
| Number | component | component | |
| 0 | 0 Hz | 4.4308 | N/A |
| 1 | 43.0664 Hz | 6.8949 | 0.9981i |
| 2 | 86.1328 Hz | -4.1572 | -1.0118i |
How can we use this information? Well, remember from the chapter on complex numbers that the magnitude of a signal – essentially, the amplitude of the signal that we see – is calculated from the real and imaginary components using the Pythagorean theorem. Therefore, in the example above, the magnitude response can be calculated by taking the square root of the sum of the squares of the real and imaginary results of the DFT. Huh? Check out Table 9.2.
| Bin Number | Frequency (Hz) | 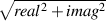 | Magnitude |
| 0 | 0 Hz |  | 4.4308 |
| 1 | 43.0664 Hz |  | 6.9668 |
| 2 | 86.1328 Hz |  | 4.2786 |
If we keep filling out this table up to the 1024th bin, and graphed the results of Magnitude vs. Bin Frequency we’d have what everyone calls the Frequency Response of the signal. This would tell us, frequency by frequency the amplitude relationship of the various harmonics in the signal. The one thing that it wouldn’t tell us is what the phase relationship of the various harmonics are. How can we calculate that? Well, remember from the chapter on trigonometry that the relative levels of the real and imaginary components can be calculated using the phase and amplitude of a signal. Also, remember from the chapter on complex numbers that the phase of the signal can be calculated using the relative levels of the real and imaginary components using the equation:
 | (9.2) |
So, now we can create a table of phase relationships, bin by bin as shown in Table 9.3:
| Bin Number | Frequency (Hz) | arctan( ) ) | Phase (degrees) |
| 0 | 0 Hz | arctan | 0∘ |
| 1 | 43.0664 Hz | arctan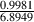 | 8.2231∘ |
| 2 | 86.1328 Hz | arctan | 13.6561∘ |
So, for example, the signal shown in Figure 3 has a component at 86.1328 Hz with a magnitude of 4.2786 and a phase offset of 13.6561∘.
Note that you’ll sometimes hear people saying something along the lines of the real component being the signal and the imaginary component containing the phase information. If you hear this, ignore it – it’s wrong. You need both the real and the imaginary components to determine both the magnitude and the phase content of your signal. If you have one or the other, you’ll get an idea of what’s going on, but not a very good one.
When you do a DFT, there’s a limit on the number of bins you can calculate. This total number is dependent on the number of samples in the audio signal that you’re using, where the number of bins equals the number of samples. Just to make computers happier (and therefore faster) we tend to do DFT’s using window lengths which are powers of 2, so you’ll see lengths like 256 points, or 1024 points. So, a 256-point DFT will take in a digital audio signal that is 256 samples long and give you back 256 bins, each containing a complex number representing the real and imaginary components of the signal.
Now, remember that the bins are evenly spaced from 0 Hz up to the sampling rate, so if you have 1024 bins and the sampling rate is 44.1 kHz then you get a bin every 44100/1024 Hz or 43.0664 Hz. The longer the DFT window, the better the resolution you get because you’re dividing the sampling rate by a bigger number and the spacing in frequency gets smaller. Intuitively, this makes sense. For example, let’s say that we used a DFT length of 4 points. At a very low frequency, there isn’t enough change in 4 samples (which is all the DFT knows about...) to see a difference, so the DFT can’t calculate a low frequency. The longer the window length, the lower the frequency we can look at. If you wanted to see what was happening at 1 Hz, then you’re going to have to wait for at least 1 full period of the waveform to understand what’s going on. This means that your DFT window length as to be at least the size of all the samples in one second (because the period of a 1 Hz wave is 1 second). Therefore, the better low-frequency resolution you want, the longer a DFT window you’re going to have to use.
This is great, but if you’re trying to do this in real time, meaning that you want a DFT of a signal that you’re listening to while you’re listening to it, then you have to remember that the DFT can’t be calculated until all of the samples in the window are known. Therefore, if you want good low-frequency resolution, you’ll have to wait a little while for it. For example, if your window size is 8192 samples long, then the first DFT result won’t come out of the system until 8192 samples after the music starts. Essentially, you’re always looking at what has just happened – not what is happening. Therefore, if you want a faster response, you need to use a smaller window length.
The moral of the story here is that you can choose between good low-frequency resolution or fast response – but you really can’t have both (but there are a couple of ways of cheating...).
If you go through the motions and do a DFT bin by bin, you’ll start to notice that the results start mirroring themselves. For example, if you do an 8-point DFT, then bins 0 up to 4 will all be different, then bin 5 will be identical to bin 3, bins 6 and 2 are the same, and bins 7 and 1 are the same. This is because the frequencies of the DFT bins go from 0 Hz to the sampling rate, but the audio signal only goes to half of the sampling rate, normally called the Nyquist frequency. Above the Nyquist, aliasing occurs and we get redundant information. The odd thing here is the fact that we actually eliminated information above the Nyquist frequency on the conversion from analog to digital, but there is still stuff there – it’s just a mirror image of the signal we kept.
Consequently, when we do a DFT, since we get this mirror effect, we typically throw
away the redundant data and keep a little more than half the number of bins
– in fact, it’s one more than half the number. So, if you do a 256-point DFT,
then you are really given 256 frequency bins, but only 129 of those are usable
(256/2 + 1). In real books on DSP, they’ll tell you that, for an N-point DFT,
you get N/2+1 bins. These bins go from 0 Hz up to the Nyquist frequency or
 .
.
Also, you’ll notice that at the first and last bins (at 0 Hz and the Nyquist frequency) only contain real values – no imaginary components. This is because, in both cases, we can’t calculate the phase. There is no phase information at 0 Hz, and since, at the Nyquist frequency, the samples are always hitting the same point on the sinusoid, we don’t see its phase.
Good question. Well, what we’ve done is to look at a signal represented in the Time domain (in other words, what does the signal do if we look at it over a period of time) and convert that into a representation in the Frequency domain (in other words, what are the represented frequencies in this signal). These two domains are completely inter-related. That is to say that if you take any signal in the time domain, it has only one representation in the frequency domain. If you take that signal’s representation in the frequency domain, you can convert it back to the time domain. Essentially, you can calculate one from the other because they are just two different ways of expressing the same signal.
For example, I can use the word “two” or the symbol “2” to express a quantity. Both mean exactly the same thing – there is no difference between “2 chairs” and “two chairs.” The same is true when you’re moving back and forth between the frequency domain and time domain representations of the same signal. The signal stays the same – you just have two different ways of writing it down.
Now that you know how a DFT is actually performed, let’s look at how the other books describe it. You’ll usually see a DFT defined using a slightly ugly equation like Equation 9.3. This actually is the mathematical representation of the process I just described, where the signal is multiplied by the real and inverted imaginary components, frequency by frequency, and the results are all added up to give a single complex number per frequency.
 | (9.3) |
where X is a discrete-time signal, n is the time in samples, and f is the frequency relative to the sampling rate
In Equation 9.3, you have a signal called X that has a number of samples in it (the
sample number is called n, so the value of the sample at time 0 is called X(0) – therefore
n = 0). The samples in signal X going from the beginning of time (n = -∞) to the end of
time (n = ∞) are multiplied by e-j2πfn (remember from Section 1.7 that this means a
cosine wave and an upside-down sine wave) at some frequency f. All of the results of
that multiplication are then added together (hence the ∑). This is done for all
frequencies between -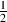 (half of the sampling rate, but rotating backwards) to
(half of the sampling rate, but rotating backwards) to
 .
.
So, the math in Equation 9.3 describes the same thing as was discussed in this chapter. It just makes things a little less accessible.
If you are doing an FFT instead of a DFT, then things are slightly different as is shown in Equation 9.4. The only real difference is that we don’t have a limitation on f. Apart from that, things are just about the same, but because we’re working with continuous time, we have to use an integral instead of a simple sum (if the difference is confusing, see Section 1.9).
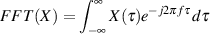 | (9.4) |
where X is a discrete-time signal, τ is the time, and f is the frequency relative to the sampling rate
Now that we know how to convert a time domain signal into a frequency domain representation, let’s try it out. We’ll start by creating a simple sine wave that lasts for 1024 samples and is comprised of nearly 4 cycles as is shown in Figure 9.12.
If we do a 1024-point DFT of this signal and show the modulus of each bin (not including the redundancy in the mirror image), it will look like Figure 9.13.
You’ll notice that there’s a big spike at one frequency and a little noise (very little... -350 dB is a VERY small number) in all of the other bins. In case you’re wondering, the noise is caused by the limited resolution of MATLAB which I used for creating these graphs. MATLAB calculates numbers with a resolution of 64 bits (floating point). That gives us a dynamic range of about 385 dB or so to work with – more than enough for this textbook... More than enough for most things, actually...
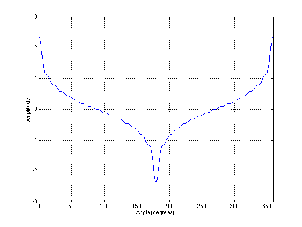
Now, what would happen if we had a different frequency? For example, Figure 9.14 shows a sine wave with a frequency of 0.875 times the one in Figure 9.12.
If we do a 1024-point DFT on this signal and just look at the modulus of the result, we get the plot shown in Figure 9.15.
You’ll probably notice that Figure 9.13 is very different from Figure 9.15. We can tell from the former almost exactly what the signal is, and what it isn’t. In the latter, however, we get a big mush of information. We can see that there’s more information in the low end than in the high end, but we really can’t tell that it’s a sine wave. Why does this happen?
The problem is that we’ve only taken a slice of time. When you do a DFT, it assumes that the time signal you’re feeding it is periodic. Let’s make the same assumption on our two sine waves shown above. If we take the first one (shown in Figure 9.12) and repeat it, it will look like Figure 9.16. You can see that the repetition joins smoothly with the first presentation of the signal, so the signal continues to be a sine wave. If we kept repeating the signal, you’d get smooth connections between the signals and you’d just make a longer and longer sine wave. In other words, as far as the computer knows, the sine wave that it’s analysing started at the beginning of time, it will continue until the end of time, and it will always be a sine wave.
If we take the second sine wave (shown in Figure 9.14) and repeat it, we get Figure 9.17. Now, we can see that things aren’t so pretty. Because the length of the signal is not an integer number of cycles of the sine wave, when we repeat it, we get a nasty-look change in the sine wave. In fact, if you look at Figure 9.17, you can see that it can’t be called a sine wave any more. It has some parts that look like a sine wave, but there’s a spike in the middle. If we keep repeating the signal over and over, we’ve get a spike for every repetition.
That spike (also called a discontinuity) in the time signal contains energy in frequency bins other than where the sine wave is. in fact, this energy can be seen in the DFT that we did in Figure 9.15.
The moral of the story thus far is that if your signal’s period is not the same length as 1 more sample than the window of time you’re doing the DFT on, then you’re going to get a strange result. Why does it have to be 1 more sample? This is because if the period was equal to the window length, then when you repeated it, you’d get a repetition of the signal because the first sample in the window is the same as the last. (In fact, if you look carefully at the end of the signal in Figure 9.12, you’ll see that it doesn’t quite get back to 0 for exactly this reason.
How do we solve this problem? Well, we have to do something to the signal to make sure that the nasty spike goes away when we “repeat” it. The concept is basically the same as doing a crossfade between two sounds – we’re just going to make sure that the signal in the window starts at 0, fades in, and then fades away to 0 before we do the DFT. We do this by introducing something called a windowing function. This is a time-dependent gain that is multiplied by our signal as is shown in Figure 9.18.
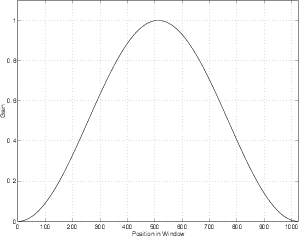
Let’s take the signal in Figure 9.14 – the one that caused us all the problems. If we multiply each of the samples in that signal with its corresponding gain shown in Figure 9.18, then we get a signal that looks like the one shown in Figure 9.19.
You’ll notice that the signal still has the sine wave from Figure 9.14, but we’ve changed its level over time so that it starts and ends with a 0 value. This way, when we repeat it, the ends join together seamlessly. Now, if we do a 1024-point DFT on this signal we get Figure 9.20.
Okay, so the end result isn’t perfect, but we’ve attenuated the junk information by as much as 100 dB, which, if you ask me is pretty darned good.
Of course, like everything in life, this comes at a cost. What happens if we apply the same windowing function to the well-behaved signal in Figure 9.12 and do a DFT? The result will look like Figure 9.21.
So, you can see that applying the windowing function made bad things better but good things worse. The moral here is that you need to know that using a windowing function will have an effect on the output of your DFT calculation. Sometimes you should use it, sometimes you shouldn’t. If you don’t know whether you should or not, you should try it with and without and decide which worked best.
So, we’ve seen that applying a windowing function will change the resulting frequency response. The good thing is that this change is predictable, and different for different functions, so you can not only choose whether or not to window your signal, but you can also choose what kind of window to use according to your requirements.
There are essentially an infinite number of different windowing functions available for you, but there are a number of standard ones that everyone uses for different reasons. We’ll look at only a small number of them to avoid making the book longer than it needs to be...
The rectangular window is the simplest of all the windowing functions because you don’t have to do anything. If you multiply each value in your time signal by 1 (in other words, do nothing to your signal) then your gain function will look like Figures 9.23 to 9.26, depending on how long your window is. These graphs look like rectangles, so we call “doing nothing” or “multiplying by 1” a “rectangular window”. (Some folks call this a “Dirichlet window” after the German mathematician Johann Peter Gustav Lejeune Dirichlet1
Now, let’s do something a little strange. Let’s pretend for a while that the windowing function in Figure 9.23 is actually an audio signal and let’s look at its spectrum – in other words, if you sent that signal to a loudspeaker, what is its frequency content? We can find this out by doing a DFT of the signal, which results in the general response shown in Figure 9.27.
Notice that the frequency axis of this plot is shown as a multiple of the sampling rate, going from 0 Hz (DC) to the Nyquist frequency (0.5 * the sampling rate). This makes some intuitive sense, since the time signal (1) has only positive values (therefore it has to have some DC component keeping it above 0...) and (2) is two 1’s in a row - therefore anything at the Nyquist (which would be going positive and negative on adjacent samples) will not exist.
If we do the same for Figures 9.24 to 9.26 we get the magnitude responses shown in Figures 9.28 to 9.30. You might be curious to note that there half as many notches in the magnitude responses as there are samples in the time signals. This is not really very important – it’s just interesting...
So, you can see that the spectral content of a rectangular windowing function (in other words, a signal with a bunch of 1’s in a row) has a weird behaviour with a lot of notches in it – the longer the window length, the more notches we have. This also means that, the longer the window length, the more closely the notches are spaced in frequency.
Here’s where things get a little weird... If we take a portion of a sine wave and multiply it by a rectangular windowing function (in other words, do nothing to it...) and do a DFT of the result, we’ll see something strange that we’ve already learned to expect... sort of... What we’ll see is that, although the sine wave should consist of energy at only one frequency, the DFT will probably tell us that there’s energy in lots of other frequency bins (unless, as we already saw, that the sine wave has exactly the same frequency as the centre frequency of one of the DFT bins – but this is a special case that never happens in the wild). What we’ll see is energy from the signal “leaking” into other frequency bins – an effect that is called spectral leakage.
For example, we saw back in Figure 9.15 that, if we’re not really careful or really lucky, a DFT will tell us that there is energy in frequency bins where we don’t expect it to be – that’s the spectral leakage. The nice thing is that it’s has a very predictable behaviour.
Think back to the plots in Figures 9.27 to 9.30. I said that these were magnitude plots of the spectral content of rectangular windows of different lengths, if we treated them as if they were audio signals instead of windowing functions. It turns out that these are also plots of the spectral leakage those functions will generate if we use them to window a time signal before doing a DFT of it. I’ll explain what that means...
Let’s say that we make a sine wave with a frequency of 1024 Hz, and we do a DFT of it, and it just so happens that one of our DFT bins has a centre frequency of 1024 Hz. Then, the frequency of the sine wave is the same as a bin frequency and we’ll magically get no spectral leakage. This is illustrated in Figure 9.31.
Now let’s take a case where the frequency of the sine wave is halfway between the centre frequencies of two adjacent DFT bins. What will happen? Well, since there are no DFT bins where the sine wave is (in frequency) the energy has to show up somewhere... So, it leaks all over the place. Take a look at Figure ?? which shows this case.
If the sine wave has a frequency somewhere else, then the distribution of energy in the DFT bins will change, as you can see in Figures 9.33 and 9.34.
One minor problem: I’m being a little mis-leading in Figures 9.34 to 9.34. You have to remember in these plots that the only output from the DFT will be the values of the red stars. Although the effect of the rectangular window will be the black line, the only way we see it is as discrete values for each bin.
So, now you should be able to make a small jump. Look at Figure 9.32, re-scale it in your head so that the X-axis (which, although it’s labeled “DFT bins” is really the frequency domain...) is on a logarithmic scale instead of a linear one. You should come up with a plot that is not very different from Figure 9.15. In fact, they show essentially the same thing...
So, now that we know how to “read” the Spectral Leakage plots above, let’s plough through some different types of windowing functions and discuss their effect on the results you’ll see coming out of a DFT.
As we’ve already seen, a rectangular window has the nice effect that, if your frequency content of the signal you’re analysing is exactly the same as your DFT bin frequencies, then you get a very good idea of what’s going on in the signal. However, if the frequencies don’t line up nicely (for example, if you’re using a DFT to get an idea of the spectral content of a snippet of a Bach violin partita) then you’ll get smearing all over the place, and you can’t really get much of an idea of what’s going on in anything other than a general sense.
On the other hand, a rectangular window is certainly easy to use, since you don’t have to do anything to your signal other than take a slice of it. However, if you’re going to the trouble of doing a DFT, then a bit of windowing isn’t going to hurt you...

You have already seen one other standard windowing function in Figure 9.18. This is known as a Hann window2 and is defined using the equation below [Morfey, 2001].
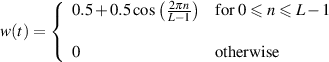
This looks a little complicated, but if you spend some time with it, you’ll see that it is exactly the same math as a cardioid microphone. It says that, within the window, you have the same response as a cardioid microphone (replacing the angle of incidence in the microphone with the time within the window), and outside the window, the gain is 0.3 This is shown in Figure 9.39
The spectral leakage for a Hanning window is shown in Figure 9.40. You can see here that, compared to the rectangular window, we get much more attenuation of unwanted signals far away from the frequencies we’re interested in. But this comes at a cost...
Take a look at Figure 9.41 which shows a close-up of the spectral leakage of a Hanning window. You can see here that the centre lobe is much wider than the one we saw for a rectangular window. So, this means that, although you’ll get better rejection of signals far away from the frequencies that you’re interested in, you’ll also get more garbage leaking into DFT bins very close to those frequencies. So, if you’re interested in a broad perspective, this window might be useful, if you’re zooming in on a specific frequency, you might be better off using another windowing function.
Our next windowing function is known as the Hamming4 window. The equation for this is

This gain response can be seen in Figure 9.44. Notice that this one is slightly weird in that it never actually reaches 0 at the ends of the window, so you don’t get a completely smooth transition.
The spectral leakage caused by a Hamming window is shown in Figure 9.45. Notice that the rejection of frequencies far away from the centre is better than with the rectangular window, but worse than with the Hanning function.
So, why do we use the Hamming window instead of the Hanning if its rejection is worse away from the 0 Hz line? The centre lobe is still quite wide, so that doesn’t give us an advantage. However, take a look at the lobes adjacent to the centre in Figure 9.46. Notice that these are quite low, and very narrow, particularly when they’re compared to the other two functions. We’ll look at them side-by-side in one graph a little later, so no need to flip pages back and forth at this point.
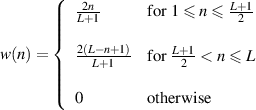
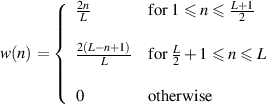

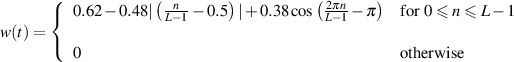


where
a0 = 0.35875
a1 = 0.48829
a2 = 0.14128
a3 = 0.01168

where
a0 = 0.3635819
a1 = 0.4891775
a2 = 0.1365995
a3 = 0.0106411
NOTES:
Also known as a tapered cosine window
The Tukey window is an interesting one, since it’s actually a family of windows.
When α = 0, then a Tukey window is a rectangular window. When α = 1, then a Tukey window is a Hann window.

x is linspace(0,L-1)
There are lots more windowing functions such as Bohman, and Parzen (also known as “de la Valle-Poussin”).
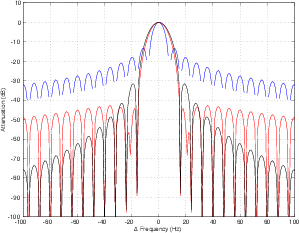
Figure 9.76 shows the three standard windows compared on one graph. As you can see, the rectangular window in blue has the narrowest centre lobe of the three, but the least attenuation of its other lobes. The Hanning window in black has a wider centre lobe but good rejection of its other lobes, getting better and better as we get further away in frequency. Finally, the Hamming window in red has a wide centre lobe, but much better rejection in its adjacent lobes.
There’s a rather basic problem that we’ve been dancing around for the past two chapters. As we’ve now seen, a Fourier Transform is a great tool if you have a time-domain signal and you want to get an idea of its spectral content. However, you’ll only get an idea – you won’t know anything accurately... The basic problem is that, in order to have precision in the frequency domain, you’ll need to take a very long slice of time... The more precision you want in frequency, the longer you’ll have to wait for the answer. Of course, this means that if you want to take a very short slice of time (say, the impulse response of a loudspeaker before the first wall reflection arrives at your microphone, for e example...) then your “cost” is pretty bad resolution in the frequency domain. In other words, you can’t have good time resolution and frequency resolution in the same measurement. One is the cost for getting the other. This problem is a part of what is known as the Gabor Limit or the Heisenberg-Gabor Limit.5
An additional problem associated with the Gabor Limit is that a signal can be either time-limited or band-limited, but it cannot simultaneously be both. This is intuitively seen in Figured 9.14 and 9.15 where it’s sort-of shown that, by taking a slice of a sine wave, you “create” a signal that has an infinite frequency bandwidth.
We’ve now seen in Sections 9.2 that there is a direct link between the time domain and the frequency domain. If we make a change in a signal in the time domain, then we must incur a change in the frequency content of the signal. Way back in the section on analog filters we looked at how we can use the slow time response of a capacitor or an inductor to change the frequency response of a signal passed through it.
Now we are going to start thinking about how to intentionally change the frequency response of a signal by making changes to it in the time domain digitally.
We’ve already seen back in Section 3.2.4 that a comb filter is an effect that is caused when a signal is mixed with a delayed version of itself. This happens in real life all the time when a direct sound meets a reflection of the same sound at your eardrum. These two signals are mixed acoustically and the result is a change in the timbre of the direct sound.
So, let’s implement this digitally. This can be done pretty easily using the block diagram shown in Figure 9.77 which corresponds to Equation 9.5.
![y[t]= a0x[t]+ a1x[t- k]](intro_to_sound_recording820x.png) | (9.5) |
This implementation is called a Finite Impulse Response comb filter or FIR comb filter because, as we’ll see in the coming sections, its impulse response is finite (meaning it ends at some predictable time) and that its frequency response looks a little like a hair comb.
As we can see in the diagram, the output consists of the addition of two signals, the original input and a gain-modified delayed signal (the delay is the block with the z-k in it. We’ll talk later about why that notation is used, but for now, you’ll need to know that the delay time is k samples.). Let’s assume for the remainder of this section that the gain value a is between -1 and 1, and is not 0. (If it was 0, then we wouldn’t hear the output of the delay and we wouldn’t have a comb filter, we’d just have a “through-put” where the output is identical to the input.)
If we’re thinking in terms of acoustics, the direct sound is simulated by the non-delayed signal (the through-put) and the reflection is simulated by the output of the delay.
Let’s take an FIR comb filter as is described in Figure 9.90 and Equation 9.5 and make the delay time equal to 1 sample, and a = 1. What will this algorithm do to an audio signal?
We’ll start by thinking about a sine wave with a very low frequency – in this case the phase difference between the input and the output of the delay is very small because it’s only 1 sample. The lower the frequency, the smaller the phase difference until, at 0 Hz (DC) there is no phase difference (because there is no phase...). Since the output is the addition of the values of the two samples (now, and 1 sample ago), we get more at the output than the input. At 0 Hz, the output is equal to exactly two times the input. As the frequency goes higher, the phase difference caused by the delay gets bigger and the output gets smaller.
Now, let’s think of a sine wave at the Nyquist frequency (see Section 8.1.3 if you need a definition). At this frequency, a sample and the previous sample are separated by 180∘, therefore, they are identical but opposite in polarity. Therefore, the output of this comb filter will be 0 at the Nyquist Frequency because the samples are cancelling themselves. At frequencies below the Nyquist, we get more and more output from the filter.
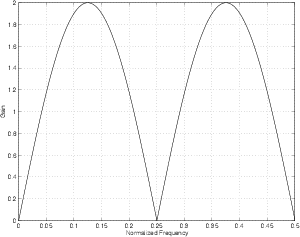
If we were to plot the resulting frequency response of the output of the filter it would look like Figure 9.78. (Note that the plot uses a normalized frequency, explained in Section 9.1.2.)
What would happen if the delay in the FIR comb filter were 2 samples long? We can think of the result in the same way as we did in the previous description. At DC, the filter will behave in the same way as the FIR comb with a 1-sample delay. At the Nyquist Frequency, however, things will be a little different... At the Nyquist frequency (a normalized frequency of 0.5), every second sample has an identical value because they’re 360∘ apart. Therefore, the output of the filter at the Nyquist Frequency will be two times the input value, just as in the case of DC.
At one-half the Nyquist Frequency (a normalized frequency of 0.25) there is a 90∘ phase difference between samples, therefore there is a 180∘ phase difference between the input and the output of the delay. Therefore, at this frequency, our FIR comb filter will have no output.
The final frequency response is shown in Figure 9.79.
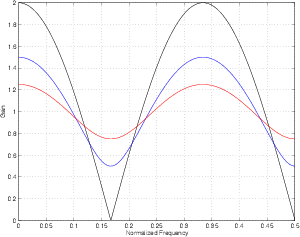
As we increase the delay time in the FIR comb filter, the first notch in the frequency response drops lower and lower in frequency as can be seen in Figures 9.80 and 9.81.
Up to now, we have been looking at the frequency response graphs on a linear scale. This has been to give you an idea of the behaviour of the FIR comb filter in a mathematical sense, but it really doesn’t provide an intuitive feel for how it will sound. In order to get this, we have to plot the frequency response on a semi-logarithmic plot (where the X-axis shows the frequency on a logarithmic scale and the Y-axis is on a linear scale). This is shown in Figure 9.82.

So far, we have kept the gain on the output of the delay at 1 to make things simple. What happens if this is set to a smaller (but still positive) number? The bumps and notches in the frequency response will still be in the same places (in other words, the won’t change in frequency) but they won’t be as drastic. The bumps won’t be as big and the notches won’t be as deep.


In the previous section we limited the value of the gain applied to the delay component to positive values only. However, we also have to consider what happens when this gain is set to a negative value. In essence, the behaviour is the same, but we have a reversal between the constructive and destructive interferences. In other words, what were bumps before become notches, and the notches become bumps.
For example, let’s use an FIR comb filter with a delay of 1 sample and where a0 = 1, and a1 = -1. At DC, the output of the delay component will be identical to but opposite in polarity with the non-delayed component. This means that they will cancel each other and we get no output from the filter. At a normalized frequency of 0.5 (the Nyquist Frequency) the two components will be 180∘ out of phase, but since we’re multiplying one by -1, they add to make twice the input value.
The end result is a frequency response as is shown in Figures 9.86.
If we have a longer delay time, then we get a similar behaviour as is shown in Figure 9.87.
If the gain applied to the output of the delay is set to a value greater than -1 but less than 0, we see a similar reduction in the deviation from a gain of 1 as we saw in the examples with FIR comb filters with a positive gain delay component.
If you want to get an idea of the effect of an FIR comb filter on a frequency response, we can calculate the levels of the maxima and minima in its frequency response. For example, the maximum value of the frequency response shown in Figure 9.85 is 6 dB. The minimum value is -∞ dB. Therefore a total peak-to-peak variation in the frequency response is ∞ dB.
We can calculate these directly using Equations 9.6 and 9.7 [Martin, 2002a].
 | (9.6) |
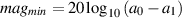 | (9.7) |
In order to find the total peak-to-peak variation in the frequency response of the FIR comb filter, we can use Equation 9.8.
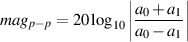 | (9.8) |
We have seen in earlier sections of this book that the time domain and the frequency domain are just two different ways of expressing the same thing. This rule holds true for digital filters as well as signals.
Back in Section 3.5.3 that we used an impulse response to find the behaviour of a string on a musical instrument. We can do the same for a filter implemented in DSP, with a little fudging here and there... First we have to make the digital equivalent of an impulse. This is fairly simple, we just have to make an infinite string of 0’s with a single 1 somewhere. Usually when this signal is described in a DSP book, we think of the “1” as happening now, therefore we see a description like Equation 9.4.3.

This digital equivalent to an impulse is called a Dirac impulse (named after Paul Dirac, an English mathematician6 ). Although in the digital domain it looks a lot like an impulse, it really isn’t because it isn’t infinitely short of infinitely loud. On the other hand, it behaved in a very similar way to a real impulse since, in the digital domain, it has a flat frequency response from DC to the Nyquist Frequency.
What happens at the output when we send the Dirac impulse through the FIR comb filter with a 3-sample delay? First, we see the Dirac come out the output at the same time it arrives at the input, but multiplied by the gain value a0 (up to now, we have used 1 for this value). Then, three samples later, we see the impulse again at the output, this time multiplied by the gain value a1.
Since nothing happens after this, the impulse response has ended (we could keep measuring it, but we would just get 0’s forever...) which is why we call these FIR (for finite impulse response) filters. If an impulse goes in, the filter will stop giving you an output at a predictable time.
Figure 9.88 shows three examples of different FIR comb filter impulse responses and their corresponding frequency responses. Note that the delay values for all three filters are the same, therefore the notches and peaks in the frequency responses are all matched. Only the value of a1 was changed, therefore modifying the amount of modulation in the frequency responses.

So far, we have only looked at one simple type of FIR filter – the FIR comb. In fact, there are an infinite number of other types of FIR filters but most of them don’t have specific names (good thing too, since there is an infinite number of them... we would spend forever naming things...).
Figure 9.89 shows the general block diagram for an FIR filter. Notice that there can be any number of delays, each with its own delay time and gain.
Since we have a class of filters that are specifically called “Finite Impulse Response” filters, then it stands to reason that they’re called that to distinguish them from another type of filter with an infinite impulse response. If you already guess this, then you’d be right. That other class is called Infinite Impulse Response (or IIR) filters for reasons that will be explained below.
We have already seen in Section 9.4.1 that a comb filter is one with a frequency response that looks like a hair comb. In an FIR comb filter, this is accomplished by adding a signal to a delayed copy of itself.
This can also be accomplished as an IIR filter, however, both the implementation and the results are slightly different.
Figure 9.90 shows a simple IIR comb filter
As can be seen in the block diagram, we are now using feedback as a component in the filter’s design. The output of the filter is fed backwards through a delay and a gain multiplier and the result is added back to the input, which is fed back through the same delay and so on...
Since the output of the delay is connected (through the gain and the summing) back to the input of the delay, it keeps the signal in a loop forever. That means that if we send a Dirac impulse into the filter, the output of the filter will be busy forever, therefore it has an infinite impulse response.
The feedback loop can also be seen in Equation 9.9 which shows the general equation for a simple IIR comb filter. Notice that there is a y on both sides of the equation – the output at the moment y[t] is formed of two components, the input at the same time (now) x[t] and the output from k samples ago indicated by the y[t -k]. Of course, both of these components are multiplied by their respective gain factors.
![y[t]= a0x[t]+ a1y[t- k]](intro_to_sound_recording838x.png) | (9.9) |
Let’s use the block diagram shown in Figure 9.77 and make an IIR comb. We’ll make a0 = 1, a1 = 0.5 and k = 3. The result of this is that a Dirac impulse comes in the filter and immediately appears at the output (because a0 = 1). Three samples later, it also comes out the output at one-half the level (because a1 = 0.5 and k = 3).
The resulting impulse response will look like Figure 9.91.
Note that, in Figure 9.91, I only plotted the first 20 samples of the impulse response, however, it in fact extends to infinity.
What will the frequency response of this filter look like? This is shown in Figure 9.92.
Compare this with the FIR comb filter shown in Figure 9.83. There are a couple of things to notice about the similarity and difference between the two graphs.
The similarity is that the peaks and dips in the two graphs are at the same frequencies. They aren’t the same basic shape, but they appear at the same place. This is due to the matching 3-sample delays and the fact that the gain applied to the delays are both positive.
The difference between the graphs is obviously the shape of the curve itself. Where the FIR filter had broad peaks and narrow dips, the IIR filter has the opposite – narrow peaks and broad dips. This is going to cause the two filters to sound very different. Generally speaking, it is much easier for us to hear a boost than a cut. The narrow peaks in the frequency response of an IIR filter are immediately obvious as audible boosts in the signal. This is not only caused by the fact that the narrow frequency bands are boosted, but that there is a smearing of energy in time at those frequencies known as ringing. In fact, if you take an IIR filter with a fairly high value of a1 – say between 0.5 and 0.999 of a0, and put in an impulse, you’ll hear a tone ringing in the filter. The higher the gain of a1, the longer the ringing and the more obvious the tone. This frequency response change can be seen in Figure 9.93.
Just like the FIR counterpart, an IIR comb filter can have a negative gain at the delay output. As can be seen in Figure 9.92, positive feedback causes a large boost in the low frequencies with a peak at DC. This can be avoided by using a negative feedback value.
The interesting thing here is that the result of the negative feedback through a delay causes the impulse response to flip back and forth in polarity as can be seen in Figure 9.94.
The resulting frequency response for this filter is shown in Figure 9.95.
IIR comb filters with negative feedback suffer from the same ringing problems as those with positive feedback as can be seen in the frequency response graph in Figure 9.96.
There is one important thing to beware of when using IIR filters. Always remember that feedback is an angry animal that can lash out and attack you if you’re not careful. If the value of the feedback gain goes higher than 1, then things get ugly very quickly. The signal comes out of the delay louder than it went it, and circulates back to the input of the delay where it comes out even louder and so on and so on. Depending on the delay time, it will take a small fraction of a second for the filter to overload. And, since it has an infinite impulse response, even if you pull the feedback gain back to less than 1, the distortion that you may have caused will always be circulating in the filter. The only way to get rid of it is to drop a1 to 0 until the delay clears out and then start again. (Although some IIR filters allow you to send a clear command, telling them to forget everything that’s happened before now, and to continue on as if you were normal. Take a look at some of the filters in Max/MSP, for example.)
While it’s fun to make comb filters to get started (every budding guitarist has a flanger or a phaser in their kit of pedal effects. The rich kids even have both and claim that they know the difference!) IIR filters can be a little more useful. Now, don’t get me wrong, FIR filters are also useful, but as you’ll see if you ever have to start working with them, they’re pretty expensive in terms of processing power. Basically, if you want to do something interesting, you have to do it for a long time (rather Zen, no?). If you have an FIR filter with a long, impulse response, then that means a lot of delays (or long ones) and lots of math to do. We’ll see a worst-case scenario in Section 9.6.1.
A simple IIR filter has the advantage of having only three operations (two multiplies and one add) and one delay, and still having an infinite impulse response, so you can do interesting things with a minimum of processing.
One of the most common building blocks in any DSP algorithm is a little package called a biquadratic filter or biquad for short. This is a sort of mini-algorithm that contains a just small number of delays, gains and additions as is shown in Figure 9.97, but it turns out to be a pretty powerful little tool – sort of the op amp of the DSP world in terms of usefulness.
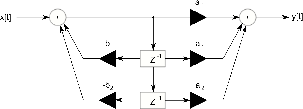
Okay, let’s look at what a biquad does, going through it, gain by gain.
The end result is an algorithm described by Equation 9.10.
![y[t]= a0x[t]+ a1x[t- 1]+ a2x[t- 2]- b1y[t- 1]- b1x[t- 2]](intro_to_sound_recording846x.png) | (9.10) |
So, what we’ve seen is that a biquad is an assembly of two FIR combs and two IIR combs, all in one neat little package. The interesting thing is that this algorithm is extremely powerful. So, I’ll bet you’re sitting there wondering what it’s used for? Let’s look at just a couple of examples.
Important Note: If you want the original version of this section, go to the original source, written by Robert Bristow-Johnson and called the Audio EQ Cookbook. You’ll find it at http://www.musicdsp.org/files/Audio-EQ-Cookbook.txt, or, if it moves, just do a search for Robert Bristow-Johnson’s “Audio EQ Cookbook”.
Before we go on, please make sure that you’ve read Section 6.1.6. It’s important – I promise!
So, if you’re still reading, let’s go on...
If you’re going to build a second-order IIR filter using a biquad, first you need to decide on some things:
No matter what type of filter you’re going to make (well... almost no matter...), you’ll need to start with a couple of basic equations shown in Equations 9.11 to 9.16.
 | (9.11) |
where gain is in dB.
 | (9.12) |
where fc is the cutoff frequency (or centre frequency in the case of peaking filters or the shelf midpoint frequency for shelving filters). Note that the frequency fc here is given as a normalized frequency between 0 and 0.5. If you prefer to think in terms of the more usual way of describing frequency, in Hertz, then you’ll need to do an extra little bit of math as is shown in Equation 9.13.
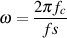 | (9.13) |
where fc is the cutoff frequency (or centre frequency in the case of peaking filters or the shelf midpoint frequency for shelving filters) in Hz and fs is the sampling rate in Hz. Important note: You should use either Equation 9.12 or Equation 9.13, depending on which way you prefer to state the frequency. However, I would recommend that you get used to thinking in terms of normalized frequency, so you should be happy with using Equation 9.12.
 | (9.14) |
Use the previous equation to convert bandwidth or bw into a Q value.
Then, if you are building a peaking filter, you use Equation 9.15.
 | (9.15) |
If you’re building a shelving filter, you use Equation 9.16.
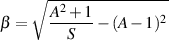 | (9.16) |
where S is a shelf slope parameter. The lower S is, the lower the slope of the steepest part in the magnitude response of the filter (at fc). If S is 1 or lower, then the slope of the magnitude response does not change polarity through the entire frequency range. For example, if you’re making a high shelving filter with a boost and S has a value of ≤ 1 then the slope of the magnitude response is positive at all frequencies. If S > 1 then the magnitude response, going from low to high frequencies, will be flat, dip in a small notch, then turn around and head up to a peak above the desired gain value, turn around again, and head down to that value.
Very Important Note regarding the definition of Q: You might remember from a Section 6.1.6 that we defined the Q of a filter using the centre frequency and the bandwidth, where the bandwidth was measured as a difference between the two frequencies that are 3 dB lower than the peak at the centre frequency. Although this is the classical definition of Q, it is not the one used here – at least for peaking and shelving filters. The Q that we’re using here is the one that says that the bandwidth is defined by the half-gain (in dB) frequency points. See Section 6.1.6 for more info.
We already know from an earlier section what a low-pass filter is. One way to implement this in a DSP chain is to insert a biquad and calculate its coefficients using the equations below.
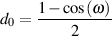 | (9.17) |
 | (9.18) |
 | (9.19) |
 | (9.20) |
 | (9.21) |
 | (9.22) |
Likewise, we could, instead, create a low-shelving filter using coefficients calculated in the equations below.
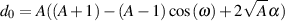 | (9.23) |
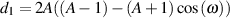 | (9.24) |
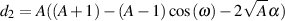 | (9.25) |
 | (9.26) |
 | (9.27) |
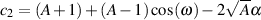 | (9.28) |
The following equations will result in a reciprocal peak-dip filter configuration.
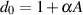 | (9.29) |
 | (9.30) |
 | (9.31) |
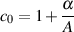 | (9.32) |
 | (9.33) |
 | (9.34) |
The following equations will produce a high-shelving filter.
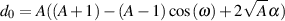 | (9.35) |
 | (9.36) |
 | (9.37) |
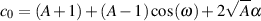 | (9.38) |
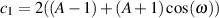 | (9.39) |
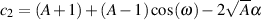 | (9.40) |
Finally, the following equations will produce a high-pass filter.
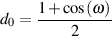 | (9.41) |
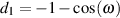 | (9.42) |
 | (9.43) |
 | (9.44) |
 | (9.45) |
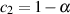 | (9.46) |
If you’re working in MATLAB or Octave, then you’ll find that, in order to build a second-order IIR filter, you’ll need three “A” coefficients and three “B” coefficients. In this case, you already have the values you want. Just use the equations below.
![a= [c c c ]
0 1 2](intro_to_sound_recording883x.png) | (9.47) |
![b = [d0 d1 d2]](intro_to_sound_recording884x.png) | (9.48) |
However, if you’re working in Max/MSP (for example...) then you only need five coefficients. This is because the coefficients are normalised and the first feedback coefficient is assumed to be 1. In order to do the normalisation for Max/MSP, then you’ll need the following equations.
 | (9.49) |
 | (9.50) |
 | (9.51) |
 | (9.52) |
 | (9.53) |
insert these values back into Equation 9.9
If you’re working in PureData, then you’re in for a bit of a confusion. See more about this in the next section.
Different software packages use different versions of Equation 9.10, resulting in much
confusion and delay.
If you’re working in MATLAB, then you use the filter function with three inputs, the a coefficients, the b coefficients, and the input signal, using the syntax
output = filter(b, a, input)
What you need to know is that the b coefficients are the feedforward and the a coefficients are the feedback. This can be seen in MATLAB’s version of Equation 9.10, shown in Equation 9.55.
![y[t]= b x[t]+ b x[t- 1]+ b x[t- 2]- a y[t- 1]- a x[t- 2]
1 2 3 1 2](intro_to_sound_recording890x.png) | (9.54) |
Notice that there are negative signs in front of the two feedback coefficients. What’s a
little odd is that this equation (from MATLAB’s user manual) isn’t really true. When you
use the filter function in MATLAB, it actually uses the a0 coefficient to normalise the
other coefficients. So, although Equation 9.55 is shown in the user manual, the actual
equation used is
![y[t]= b1x[t]+ b2x[t- 1]+ b3x[t- 2]- a1y[t- 1]- a2x[t- 2]
a0 a0 a0 a0 a0](intro_to_sound_recording891x.png) | (9.55) |
If you’re working in Max/MSP, then you use the biquad~ object with five coefficients, the a coefficients, and the b coefficients. However, Max/MSP coefficients are different from MATLAB in that the the a coefficients are the feedforward and the b coefficients are the feedback. This can be seen in Max/MSP’s version of Equation 9.10, shown in Equation 9.56.
![y[t]= a0x[t]+ a1x[t- 1]+ a2x[t- 2]- b1y[t- 1]- b2x[t- 2]](intro_to_sound_recording892x.png) | (9.56) |
Notice that, like MATLAB, there are negative signs in front of the two feedback
coefficients. However, notice that, the a’s and b’s are swapped in regards to which are
feedback and which are feedforward.
Despite having the same ancestry as Max/MSP, PureData (a.k.a. PD) uses a different syntax for its biquad~ object. Like Max/MSP, you provide five coefficients, however, the first two are the feedback coefficients, and the last three are the feedforward. To be fair, in the PD reference they are listed as fb and ff coefficients, not a and b, however, if you compare the order to the cofficients in Max/MSP, you’ll see that they’re reversed. This isn’t the only difference, since PureData uses Equation 9.57.
![y[t]= b0x[t]+ b1x[t- 1]+ b2x[t- 2]+ a1y[t- 1]+ a2x[t- 2]](intro_to_sound_recording893x.png) | (9.57) |
Okay, okay, I’ve fudged things a little here by naming them a and b instead of fb and ff – just for the purposes of comparison. However, notice that the feedback coefficients are now preceded by positives not negatives (as in MATLAB and Max/MSP). So, if you’re going to use the Robert Bristow-Johnson equations above to calculate your biquad coefficients, you’ll need to add a polarity flip on your feedback coefficients when you normalise them. If you’re porting from Max/MSP to PureData and you just drop in your biquad coefficients directly, bad, bad things will probably happen to your signal.
There is an interesting type of filter that is frequently used in DSP that we didn’t talk about very much in the chapter on analog electronics. This is the allpass filter.
As its name implies, an allpass filter allows all frequencies to pass through it without a change in magnitude. Therefore the frequency response of an allpass filter is flat. This may sound a little strange – why build a filter that doesn’t do anything to the frequency response? Well, the nice thing about an allpass is that, although it doesn’t change the frequency response, it does change the phase response of your signal. This can be useful for various situations as we’ll see below.
FINISH THIS OFF
http://www.musicdsp.org/files/Audio-EQ-Cookbook.txt
Let’s think of the most inefficient way to build an FIR filter. Back in Section 9.4 we saw a general diagram for an FIR that showed a stack of delays, each with its own independent gain. We’ll build a similar device, but we’ll have an independent delay and gain for every possible integer delay time (meaning a delay value of an integer number of samples like 4 or 13, but not 2.4 or 15.2). When we need a particular delay time, we’ll turn on the corresponding delay’s gain, and all the rest we’ll leave at 0 all the time.
For example, a smart way to do an FIR comb filter with a delay of 6 samples is shown in Figure 9.99 and Equation 9.58.

![y[t]= 1x[t]+ 0.75x[t- 6]](intro_to_sound_recording896x.png) | (9.58) |
There are stupid ways to do this as well. For example take a look at Figure 9.100 and Equation 9.59. In this case, we have a lot of delays that are implemented (therefore taking up lots of memory) but their output gains are set to 0, therefore they’re not being used.
![y[t]= 1x[t]+0x [t- 1]+0x[t- 2]+0x [t- 3]+0x [t- 4]+0x [t- 5]+0.75x[t- 6]+0x [t- 7]+0x [t- 8]](intro_to_sound_recording898x.png) | (9.59) |
We could save a little memory and still be stupid by implementing the algorithm shown in Figure 9.101. In this case, each delay is 1 sample long, arranged in a type of bucket-brigade, but we still have a bunch of unnecessary computation being done.
Let’s still be stupid and think of this in a different way. Take a look at the impulse response of our FIR filter, shown in Figure 9.102.
Now, consider each of the values in our impulse response to be the gain value for its corresponding delay time as is shown in Figure 9.100.
At time 0, the first signal sample gets multiplied by the first value in in impulse response. That’s the value of the output.
At time 1 (1 sample later) the first signal sample gets “moved” to the second value in the impulse response and is multiplied by it. At the same time, the second signal sample is multiplied by the first value in the impulse response. The results of the two multiplications are added together and that’s the output value.
At time 2 (1 sample later again...) the first signal sample gets “moved” to the third value in the impulse response and is multiplied by it. The second signal sample gets “moved” to the second value in the impulse response and is multiplied by it. The third signal sample is multiplied by the first value in the impulse response. The results of the three multiplications are added together and that’s the output value.
As time goes on, this process is repeated over and over. For each sample period, each value in the impulse response is multiplied by its corresponding sample in the signal. The results of all of these multiplications are added together and that is the output of the procedure for that sample period.
In essence, we’re using the values of the samples in the impulse response as individual gain values in a multi-tap delay. Each sample is its own tap, with an integer delay value corresponding to the index number of the sample in the impulse response.
This whole process is called convolution. What we’re doing is convolving the incoming signal with an impulse response.
Of course, if your impulse response is as simple as the one shown above, then it’s still really stupid to do your filtering this way because we’re essentially doing the same thing as what’s shown in Figure 9.101. However, if you have a really complicated impulse response, then this is the way to go (although we’re be looking at a smart way to do the math later...).
One reason convolution is attractive is that it gives you an identical result as using the original filter that’s described by the impulse response (assuming that your impulse response was measured correctly). So, if you can go down to your local FIR filter rental store, rent a good FIR comb filter for the weekend, measure its impulse response and return the filter to the store on Monday. After that, if you convolve your signals with the measured impulse response, it’s the same as using the filter. Cool huh?
The reason we like to avoid doing convolution for filtering is that it’s just so expensive in terms of computational power. For every sample that comes out of the convolver, its brain had to do as many multiplications as there are samples in the impulse response, and only one fewer additions. For example, if your impulse response was 8 samples long, then the convolver does 8 multiplications (one for every sample in the impulse response) and 7 additions (adding the results of the 8 multiplications) for every sample that comes out. That’s not so bad if your impulse response is only 8 samples long, but what if it’s something like 100,000 samples long? That’s a lot of math to do on every sample period!
So, now you’re probably sitting there thinking, “Why would I have an impulse response of a filter that’s 100,000 samples long?” Well, think back to Section 3.11 and you’ll remember that we can make an impulse response measurement of a room. If you do this, and store the impulse response, you can convolve a signal with the impulse response and you get your signal in that room. Well, technically, you get your signal played out of the loudspeaker you used to do the IR measurement at that particular location in the room, picked up by the measurement microphone at its particular placement... If you do this in a big concert hall or a church, you could easily get up to a 5 second-long impulse response, corresponding to a 220,500-sample long FIR filter at 44.1 kHz. This then means 440,999 mathematical operations (multiplications and additions) for every output sample, which in turn means 19,448,066,900 operations per second per channel of audio... That’s a lot – far more than a normal computer can perform these days.
So, here’s the dilemma, we want to use convolution, but we don’t have the computational power to do it the way I just described it. That method, with all the multiplications and additions of every single sample is called real convolution.
So, let’s think of a better way to do this. We have a signal that has a particular frequency content (or response), and we’re sending it through a filter that has a particular frequency response. The resulting output has a frequency content equivalent to the multiplication of these two frequency responses as is shown in Figure 9.103

So, we now know two interesting things:
Luckily, some smart people have figured out some clever ways to do a DFT that don’t take much computational power. (If you want to learn about this, go get a good DSP textbook and look up the word butterfly.)
So, what we can do is the following:
This procedure, called fast convolution will give you exactly the same results as if you did real convolution, however you use a lot less computational power.
There are a couple of things to worry about when you’re doing fast convolution.
FIND THIS EQUATION
 | (9.60) |
If you have a random number that lies in the range of -1 to 1 and you multiply it by a random number that lies in the same range, you’ll get a random number that lies in the same range. As we saw in Section 4.16, the result of the multiplication will have a different probability distribution function, but we’ll ignore that for now. The point for now is that a random number times a random number equals a random number.
If you now take a random number that lies in the range of -1 to 1 and multiply it by itself. you’ll get a positive number. Again, we’ll ignore the probability distribution function of the result. The point is that a random number squared is positive.
Let’s think back to the process of real convolution with the example of convolving an audio signal with the impulse response of a room. The first sample of the signal is multiplied by the first tap (sample) in the impulse response first. The two signals (the audio signal and the impulse response) move through each other until the last sample of the audio signal is multiplied by the last tap in the impulse response. This is conceptually represented in Figure 9.104.

Notice in that figure that the two signals are opposite each other – in other words, the audio signal in the diagram reads start to end from right to left while the impulse response reads from left to right.
What would happen if we did exactly the same math, but we didn’t time-reverse one of the signals? This idea is shown in Figure 9.105.

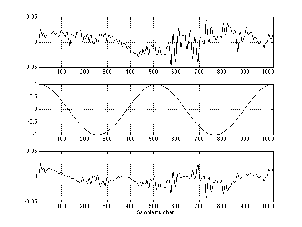
You may be asking yourself what use this could possibly be. A fair question. Let’s have a look at an example. We’ll start by looking at a series of 16 completely random numbers, shown in Figure 9.106. If I were a statistician or a mathematician, I would say that these were random numbers. If I were a recording engineer, I would call it white noise.
Let’s take that signal, and put it thought the process shown in Figure 9.105. Instead of using two different signals, we’re going to use the same signal for both. So, we start as in Figure 9.107, with the two signals lined up, ready to multiply by each other. In this case, we’re multiplying each sample by its corresponding sample (see the caption). We then add all the results of the multiplications and we get a result. In this case, since all the multiplications resulted in 0, the sum of all 32 zero’s is 0.
Once we get that result, we shift the two signals closer together by one sample and repeat the whole process, as is shown in Figure 9.108.

Then we move the signals by one sample and do it again, as is shown in Figure 9.109.

We keep doing this over and over, each time, moving the two signals by one sample and adding the results of the multiplications. Eventually, we get to a point where the signals are almost aligned as in Figure 9.110.

Then we get to a point in the process where an important thing happens. the two signals are aligned, as can be seen in Figure 9.111. Up until now, the output from each set of multiplications and additions has resulted in a fairly small number, as we’ve seen (the list of all the values that I haven’t shown will be given later...). This is because we’re multiplying random numbers that might be either positive or negative, result in numbers that might be either positive or negative, and adding them all together. (If the two signals are very long, and completely random, the result will be 0.) However, when the two signals are aligned, the result of all the individual multiplications will be positive (because any number other than 0, when multiplied by itself, gives a positive result).
If the signals are very long and random, not only will we get a result very close to zero for all other alignments, we’ll get a very big number for this middle alignment. The longer the signals, the bigger the number will be.

We keep going with the procedure, moving the signals one sample in the same direction and repeating the process, as is shown in Figure 9.112. Notice that this looks very similar to the alignment shown in Figure 9.110. In fact, the two are identical, it’s just that the top and middle graphs have swapped places, in effect. As expected, the result of the addition will be identical in the two cases.

The process continues, providing a symmetrical set of results, until the two signals have moved apart from each other, resulting in a zero again, just as we saw in the beginning.
If we actually do this process for the set of numbers initially shown in Figure 9.106, we get the following set of numbers: 0.15, 0.32, -0.02, -0.20, 0.08, -0.12, 0.01, 0.43, -0.11, 0.38, 0.02, -0.59, 0.24, -0.35, -0.02, 2.18, -0.02, -0.35, 0.24, -0.59, 0.02, 0.38, -0.11, 0.43, 0.01, -0.12, 0.08, -0.20, -0.02, 0.32, 0.15. If we then take these numbers and graph them, we get the plot shown in Figure 9.113.

The result of this whole thing actually gives us some information. Take a look at Figure 9.113, and you’ll see three important characteristics. Firstly, the signal is symmetrical. This doesn’t tell us much, other than that the signals that went through the procedure were the same. Secondly, most of the values are close to zero. This tells us that the signals were random. Thirdly, there’s a big spike in the middle of the graph, which tells us that the signals lined up and matched each other at some point.
What we have done is a procedure called autocorrelation – in other words, we’re measuring how well the signal is related (or co-related, to be precise) to itself. This may sound like a silly thing to ask – of course a signal is related to itself, right? Well, actually, no. We saw above that, unless the signals are aligned, the result of the multiplications and additions are 0. This meant that, unless the signal was aligned with itself, it is unrelated to itself (because it is noise).
What would happen if the we did the same thing, except that our original signal was periodic instead of noise? Take a look at Figure 9.114. Notice that the output of the autocorrelation still has a big peak in the middle – essentially telling us that the signal is very similar (if not identical) to itself. But you’ll also notice that the output of the autocorrelation looks sort of periodic. It’s a sinusoidal wave with an envelope. Why is this? It’s because the original signal is periodic. As the we move the signal through itself in the autocorrelation process, the output tells us that the signal is similar to itself when it’s shifted in time. So, for example, the first wave in the signal is identical to the last wave in the signal. Therefore a periodic component in the output of the autocorrelation tells us that the signal being autocorrelated is periodic – or at least that it has a periodic component.
So, autocorrelation can tell us whether a signal has periodic components. If the autocorrelation has periodic components, then the signal must as well. If the autocorrelation does not, and is just low random numbers, with a spike in the middle, then the signal does not have any periodic components.
FIND THIS EQUATION
 | (9.61) |
What if we were to do the same procedure, but instead of using one signal, we use two different signals? All of the math is the identical, we just have a different name. Because the signals are not the same, it’s not autocorrelation. Now we call it cross-correlation.
Let’s start by having two signals, and we don’t know if they’re identical or not. We can put them through the cross-correlation procedure and look at the result. If there’s a big spike in the middle, that’s a sure indication that the signals are similar, if not identical. If there is a spike, but it’s not in the middle, then the signals are similar, but not aligned. In fact, the delay difference between them can be measured by the time difference between the spike and the middle of the cross-correlation output.
This is explained in Section 4.14.
Before reading this section,if you’re not completely familiar with the idea of a correlation coefficient, you should go back and read Section 4.14.
We saw in the discussion of a correlation coefficient that this is a number that can tell us how two signals are related to each other. If the signals are completely random, then their correlation coefficient gives us a very good idea of how similar they are. However, if the signals are (in a worst-case scenario) sinusoidal waves, then the correlation coefficient can give us a very incorrect impression of what’s really going on. In addition, the correlation coefficient is a single number that doesn’t tell us what’s going on in different frequency bands.
If we want to get a better idea of the similarity of two signals in different frequency bands, we can use a different function called the coherence function (also known as a cross-power spectral density function or CPSD). This is considerably more complicated than calculating the correlation coefficient, but in some cases, the two produce related results.
Let’s say that we have two signals that we’ll call X and Y . We start by doing an autocorrelation of each of these signals, so we have RXX and RYY . Then we do a cross-correlation of the two signals, giving us RXY . Then, we do an DFT of each of these, giving us SXX (the DFT of the autocorrelation of X), SYY , and SXY (the DFT of the cross-correlation of X and Y ). Remember that the outputs of the DFT’s give us complex information in each frequency bin, so we can know the magnitude and phase of each bin.
FINISH THIS OFF - THE COHERENCE FUNCTION IS A CROSS CORRELATION THAT HAS BEEN NORMALIZED USING THE PRODUCT OF THE TWO AUTOCORRELATIONS. AVERAGE FFT OF THE NORMALIZED CROSS-CORRELATION. THIS TELLS US THE RELATIONSHIP BETWEEN THE PHASES. IF THE PHASES ARE IDENTICAL
THE FOLLOWING IS NOTES TO SELF
Given two signals, x(t) and y(t) (where t is time), the coherence of these two signals ρxy2(f) at a given frequency f can be calculated using Equation 9.62 [Shanmugan and Breipohl, 1988].
 | (9.62) |
Gxy(f) is the one-sided cross-power spectral density function calculated using Equation 9.63 [Shanmugan and Breipohl, 1988].
 | (9.63) |
Gxx(f) is the one-sided autospectral density function calculated using Equation 9.64 [Shanmugan and Breipohl, 1988].
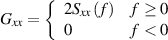 | (9.64) |
Sxy(f) is the cross-power spectral density function (also known as the cross spectrum) of x(t) and y(t). This is the Fourier transform of the cross-correlation of x(t) and y(t) and is calculated using Equation 9.65 [Bendat and Piersol, 1980]
 | (9.65) |
Sxx(f) is the autospectral density function (also known as the autospectrum or the power spectral density function) of x(t). This is the Fourier transform of the autocorrelation of x(t) and is calculated using Equation 9.66 [Bendat and Piersol, 1980].
 | (9.66) |
where τ is a time offset applied to x(t) and y(t); and Rxy(τ) is the cross-correlation function of x(t) and y(t), calculated using Equation 9.67 [Bendat and Piersol, 1980].
 | (9.67) |
where T is the record length of the signal; τ is a time offset applied to x(t) and itself; Rxx(τ) is the autocorrelation function of x(t), calculated using Equation 9.68 [Bendat and Piersol, 1980].
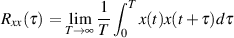 | (9.68) |
The coherence ρxy2(f) is a value that can range from 0 to 1. If the two signals x(t) and y(t) are completely independent, then they will have a coherence of 0 at all frequencies except f0 = 0 Hz. If ρxy2(fn) = 0, then the two signals are said to be incoherent at frequency fn. Conversely, if ρxy2(fn) = 1, the two signals are said to be fully coherent at frequency fn [Shanmugan and Breipohl, 1988].
The primary advantage of using the coherence function over a correlation coefficient is that it does not produce misleading results when the signals are periodic. For example, in the case of two sinusoidal waveforms with identical frequency and a phase offset of 90∘, their correlation coefficient will be 0, however, the coherence for the two signals will be 1 at the frequency of the sinusoid.
However, this example is also is an indicator of the disadvantage of using the coherence function. In the case of periodic signals, phase differences are not reflected. This is also true of polarity inversions, typically considered as a phase rotation of 180∘. For example, given two signals that are identical except for polarity the correlation coefficient of the two signals will be -1 whereas the coherence of the two signals will be 1 at all frequencies. The former indicates that the two signals are identical, but opposite in polarity. The coherence function simply indicates that the two signals are linearly related [Morfey, 2001].
So far, we have seen that digital audio means that we are taking a continuous signal and slicing it into discrete time for transmission, storage, or processing. We have also seen that we can do some math on this discrete time signal to determine its frequency content. We have also seen that we can create digital filters that basically consist of three simple building blocks, addition, multiplication and delay, which can be used to modify the signal.
What we haven’t yet seen, however, is how to figure out what a filter does, just by looking at its structure. Nor have we talked about how to design a digital filter. This is where this chapter will come in handy.
One note of warning... This whole chapter is basically a paraphrase of a much, much better introduction to digital signal processing by Ken Steiglitz [Steiglitz, 1996]. If you’re really interested in learning DSP, go out and buy this book.
Okay, to get started, let’s do a little review. The next couple of equations should be burnt into your brain for the remainder of this chapter, although I’ll bring them back now and again to remind you.
The first equation is the one for radian frequency, discussed in Section 3.1.11.
 | (9.69) |
where f is the normalized frequency (where DC = 0, the Nyquist frequency is 0.5 and the sampling rate is 1) and ω is the radian frequency in radians / samples. Notice that we’re measuring time in samples, not in seconds. Unfortunately, our DSP computer can’t tell time in seconds, it can only tell time in samples, so we have to accommodate. Therefore, whenever you see a time value listed in this section, it’s in samples.
Another equation that you probably learned in high school, and should have read back in Section 1.3 states that
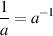 | (9.70) |
The next equation, which we saw in Section 1.7 is called Euler’s Identity. This states that
 | (9.71) |
You might notice that I made a slight change in Equation 9.71 compared with Equation 1.76 in that I replaced the θ with an ωt to make things a little easier to deal with in the time domain. Remember that ω is just another way of thinking of frequency (see section 3.1.11) and t is the time in samples.
We have to make a variation on this equation by adding an extra delay of k samples:
 | (9.72) |
You should also remember that we can play with exponents as follows:
Another basic equation to remember is the following
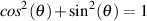 | (9.75) |
for any value of θ
Therefore, if we make a plot where the x-axis is the value of cos(θ) and the y-axis is the value of sin(θ) and we plot all the angles from 0 to 2π (or 0∘ to 360∘), we get a circle. (Go back to the discussion on Pythagoras in Section 1.2 if this isn’t obvious.)
If we put a j in front of the sin2(θ) in the equation (so it looks like cos2(θ)+jsin2(θ)) a similar thing happens. This means that the sin2(θ) component is now imaginary, and can’t be mixed with the cos2(θ). We can still use this equation to draw a perfect circle, but now we’re using a real and an imaginary axes as we saw back in Figure 1.6.13.
Okay... that’s about it. Now we’re ready.
Let’s take a very simple filter, shown in Figure 9.115 where we add the input signal to a delayed version of the input signal that has been delayed by k samples and multiplied by a gain of a1.

We have already seen that this filter can be written as Equation 9.76:
![y[t]= x= [t]+ a1x[t- k]](intro_to_sound_recording929x.png) | (9.76) |
Let’s put the output of a simple phasor into the input of this filter. A phasor is just a sinusoidal wave generator that is “thinking” in terms of a rotating wheel, therefore it has a real and imaginary component. Consequently, we can describe the phasor’s output using cos(ωt)+jsin(ωt), which, as we saw above can also be written as ejωt.
Since the output of that phasor is connected to the input of the filter then
![jωt
x[t]= e](intro_to_sound_recording930x.png) | (9.77) |
Therefore, we can rewrite Equation 9.76 for the filter as follows:
This last equation is actually pretty interesting. Remember that the input, x[t] is equal to ejωt. So what? Well, this means that we can think of the equation as is shown in Figure 9.116.
Notice that the end of Equation 9.80 has a lot of ω’s in it. This means that it is frequency-dependent. We already know that if you multiply a signal by something, that “something” is gain. We also know that if that gain is dependent on frequency (meaning that it is different at different frequencies) then it will change the frequency response. So, since we know all that, we should also see that the “what the input is multiplied by to get the output” part of Equation 9.80 is a frequency-dependent gain, and therefore is a mathematical description of the filter’s frequency response.
Please make sure that this last paragraph made sense before you move on...
Let’s be lazy and re-write Equation 9.80 a little simpler. We’ll invent a symbol that means “the frequency response of the filter.” We know that this will be a frequency-dependent function, so we’ll keep an ω in there, so let’s use the symbol H(ω). Although, if we need to describe another filter, we can use a different letter, like G(ω) for example...
We know that the frequency response of our filter above is 1+a1e-jωk and we’ve already decided that we’re going to use the general symbol H(ω) to replace that messy math, but just to make things clear, let’s write it down...
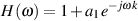 | (9.81) |
One important thing to notice here is that the above equation doesn’t have any t’s in it. This means that it is not dependent on what time it is, so it never changes. This is what is commonly known as a Linear Time Invariant or LTI system. This means two things. The “linear” part means that everything that comes in is treated the same way, no matter what. The “time invariant” part means that the characteristics of the filter never change (or vary) over time.
Things are still a little complicated because we’re still working with complex numbers, so let’s take care of that. We have seen that the reason for using complex notation is to put magnitude and phase information into one neat little package (see Section 1.6 for this discussion.) We have also seen that we can take a signal represented in complex notation and pull the magnitude and phase information back out if we must. This can also be done with H(ω) (the frequency response) of our filter. The equation below is a general form showing how to do this.
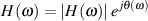 | (9.82) |
This divides the frequency response H(ω) into the filter’s magnitude response
 (see Section ?? if you need some info on getting the magnitude response) and the
phase shift θ(ω) at frequency ω. Be careful here not to jump to conclusions! The
phase shift is not θ, it’s θ(ω) but we can calculate to make a little more sense
intuitively.
(see Section ?? if you need some info on getting the magnitude response) and the
phase shift θ(ω) at frequency ω. Be careful here not to jump to conclusions! The
phase shift is not θ, it’s θ(ω) but we can calculate to make a little more sense
intuitively.
 | (9.83) |
Where the symbols ℑ means “The imaginary component of...” and ℜ means “The real component of...”
Don’t panic – it’s not so difficult to see what the real and imaginary components of the H(ω) are because the imaginary components have a j in them. For example, if we look at the filter that we started with at the beginning of this chapter, its frequency response was:
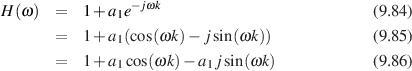
So this means that
 | (9.87) |
and
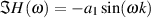 | (9.88) |
Notice that I didn’t put the j in there because I don’t need to say that it’s imaginary... I already know that it’s the imaginary component that I’m looking for.
So, to calculate the phase of our example filter, we just put those two results into Equation 9.83 as follows:

Let’s look at an even simpler example before we go too much further. Figure 9.117 shows a simple delay line of k samples with the result multiplied by a gain factor of a1.
This delay can be expressed as the equation:

As you’ve probably noticed by noticed by now, we tend to write ejω a lot, so let’s be lazy again and use another symbol instead – we’ll use z, therefore
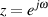 | (9.93) |
What if you want to write a delay, as in e-jωk? Well, we’ll just write (you guessed it...) z-k. Therefore z-2 is a 2-sample delay because e-jω2 is a 2-sample delay as well.
Always remember that z is a complex variable. In other words,

Therefore, we can plot the value of z on a Cartesian graph with a real and an imaginary axis, just like we’re always been doing.
Let’s take a signal and send it through two gain functions connected in series as is shown in Figure 9.118.
We can think of this as two separate modules as is shown in Figure 9.119.
So, let’s calculate how yt relates to xt. Using Figure 9.119, we can write the following equations:
![w[t] = a x[t]
0](intro_to_sound_recording947x.png) | (9.96) |
and
![y[t]= a1w[t]](intro_to_sound_recording948x.png) | (9.97) |
Therefore
![y[t] = a1w[t] (9.98)
= a1(a0x[t]) (9.99)
= a0a1x[t] (9.100)](intro_to_sound_recording949x.png)
What I took a long while to say here is that, if you have two gain stages (or, more generally, two filters) connected in series, you can multiply the effects that they have on the input to find out the output.
So far, we have been thinking in terms of the instantaneous value of each sample, sample by sample. That’s why we have been using terms like x[t] and y[t] – we’ve been quite specific about which sample we’re talking about. However, since we’re dealing with LTI systems, we can say that the same thing happens to every sample in the signal. Consequently, we don’t have to think in terms of individual samples going through the filter, we can think of the whole signal (say, a Johnny Cash tune, for example). When we speak of the whole signal, we use things like X and Y instead of x[t] and y[t]. That whole signal is what is called an operator.
In the case of the last filter we looked at (the one with the two gains in series shown in Figure 9.118), we can write the equation in terms of operators.
![Y = [a0a1]X](intro_to_sound_recording950x.png) | (9.101) |
In this case, we can see that the operator X is multiplied by a0a1 in order to become Y. This is a simple way to think of DSP if you’re not working in real time. You take the Johnny Cash tune on your hard disc. Multiply its contents by a0a1 and you get an output, which is a Johnny Cash tune at a different level (assuming that a0a1≠1).
That thing that the input operator is multiplied by is called the transfer function of the
filter and is represented by the symbol H(z). So, the transfer function of our previous
filter is a0a1. In other words, H(z) = ![[a0A1]](intro_to_sound_recording951x.png)
Notice that the transfer function in the equation is held in square brackets.
Let’s look at another simple example using two 1-sample delays connected in series as is shown in Figure 9.121
The equation for this filter would be
![y[t] = x[t]z- 1z- 1 (9.102)
- 2
= x[t]z (9.103)](intro_to_sound_recording954x.png)
and therefore
![[ ]
Y = X z-2](intro_to_sound_recording955x.png) | (9.104) |
Notice that I was able to simply multiply the two delays z-1 and z-1 together to get z-2. This is one of the slick things about using z-k to indicate a delay. If you multiply them together, you just add the exponents, therefore adding the delay times.
Let’s do one more filter before moving on...
Figure 9.122 shows a fairly simple filter which adds a gain-modified version of the input with a delayed, gain-modified version of the input.

The equation for this filter is
![y[t] = a0x[t]+ a1x[t- k] (9.105)
= a0x[t]+ a1z- kx[t] (9.106)
( -k)
= a0+ a1z x[t] (9.107)](intro_to_sound_recording957x.png)
Therefore
![[ -k]
Y = a0+ a1z X](intro_to_sound_recording958x.png) | (9.108) |
and so a0 +a1z-k is the transfer function of the filter.
Let’s take this a step further. We’ll build a big filter out of two smaller filters as is shown in Figure 9.123. The transfer function G(z) = a0 +a1z-1 while the transfer function H(z) = b0 +b1z-1.
 | (9.109) |
 | (9.110) |
Therefore

Therefore
![y[t]= a0b0x[t]+ (a0b1+ b0a1)x[t- 1]+ a1b1x[t- 2]](intro_to_sound_recording963x.png) | (9.115) |
In other words, we could implement exactly the same filter as is shown in Figure 9.124. Then again, this might not be the smartest way to implement it. Just keep in mind that there are other ways to get the same result. We know that these will give the same result because their mathematical expressions are identical.
The thing to notice about this section was the way I manipulated the equation for the cascaded filters. I just treated the notation as if it was a polynomial straight out of a high-school algebra textbook. The cool thing is that, as long as I don’t screw up, every step of the way describes the same filter in an understandable way (as long as you remember what z-k means...).
Let’s go back to a simpler filter as is shown in Figure 9.125.
This gives us the equation
 | (9.116) |
If we write this out the “old way” – that is, before we knew about the letter z, the equivalent would look like this:
![y = ejωt+ a ejωte-jω (9.117)
t [ 1-jω] jωt
= 1+ a1e e (9.118)](intro_to_sound_recording967x.png)
So 1+a1e-jω is “what the filter does” to the input ejωt. Think of 1+a1e-jω as a function of frequency. It is complex (therefore it causes a phase shift in the signal). Consequently, we say that it is a complex function of ω. In the z-domain, the equivalent is 1-a1z-1.
So, since we know that
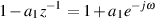 | (9.119) |
then we can say that
 | (9.120) |
In other words, the transfer function is the same as the frequency response of the filter.
We know that the transfer function of this filter is 1-a1z-1. You should also
remember that  = z-1. Therefore,
= z-1. Therefore,
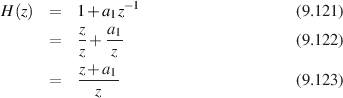
Okay, now I have a question. What values in the above equation make the numerator (the top part of the fraction) equal to 0. The answer, in this particular case is z = -a1. If the filter had been different, we would have gotten a different answer. (For e different filter we might have gotten more than one answer... but that comes later.) Notice that if the numerator is 0, then H(z) = 0. This will be important later.
Another question: What values will make the denominator (the bottom part of the equation) equal to 0? The answer, in this particular case is z = 0. Again, it might have been possible (with a different filter) to get more than one answer. Notice in this case, that if the denominator is 0, then H(z) = ∞.
Let’s graph z on a cartesian plot. We’ll make the x-axis the real axis where we plot the real component of z, and the y-axis is the imaginary axis.
We know that

We also know that
 | (9.126) |
for any value of ω.
Therefore, if we make a Cartesian plot of z then we get a circle with a radius of 1 as is shown in Figure 9.126. Notice that the amount of rotation corresponds to the radian frequency, starting at DC where z = 1 (notice that there is no imaginary component) and going to the Nyquist frequency at z = -1. When z = j1, we are at a normalized frequency of 0.25, or one-quarter of the sampling rate. This might not make sense yet, but stick with me for a while.

If it doesn’t make sense, it might be because the problem is that it appears that we are confusing frequency and phase. However, in one sense, they are directly connected, because we are describing frequency in terms of radians per sample instead of the more usual complete cycles of the waveform per second. Normally we describe the frequency of a waveform by how many complete cycles go by each second. For example, we say “a 1 kHz tone” meaning that we get 1000 complete cycles each second. Alternatively, we could say “360000 degrees per second” which says the same thing. If we counted faster than a second, then we would say something like “360 degrees per millisecond” or “0.36 degrees per microsecond.” These all say the same thing. Notice that we’re using the rate of change of the phase to describe the frequency, just like we do when we use ω.
If we back up a bit to the last filter we were working on, we said that its transfer function was
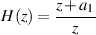 | (9.127) |
We can therefore easily calculate the magnitude of H(z) using the equation:
 | (9.128) |
An important thing to remember here is that, when you’re dealing with complex numbers, as we are at the moment, the bars on the sides of the values do not mean “the absolute value of...” as they normally do. They mean “the magnitude of...” instead. Also remember that you calculate the magnitude by finding the hypotenuse of the triangle where the real and imaginary components are the other two sides.
Since
 | (9.129) |
and
 | (9.130) |
and, because of Pythagoras
 | (9.131) |
then
 | (9.132) |
So, this means that

We found out from our questions and answers at the end of Section 9.7.6 that (for our filter that we’re still working on) H(z) = 0 when z = 1. CHECK THIS LAST SENTENCE... Let’s then mark that point with a “0” (a zero) on the graph of the z-plane. Note that a1 has only a real component, therefore -a1 has only a real component as well. Consequently, the “0” that we put on the graph sits right on the real axis.
Here’s where things get interesting (finally!). The magnitude response (what most normal people call the frequency response) of this filter can be found by measuring the distance from the “0” that we plotted to the circle on the graph. See Figure 9.128
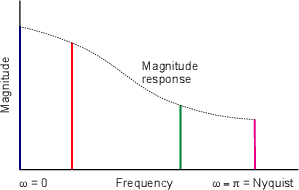
You might be sitting there wondering “what happens if I have more than one zero on the plot?” This is actually pretty simple, you just pick a value for ω, then measure the distance from each zero on the plot to the frequency ω. Then you multiply all your distances together, and the result is the magnitude response of the filter at that frequency.
There is another, possibly more intuitive way of thinking about this. Cut a circle out of a sheet of heavy rubber, and magically suspend it in space. The circle directly corresponds to the z-plane. If you have a zero on the z-plane, you push the rubber down with a pointy stick as far as possible, preferably infinitely. This will put a dent in the rubber that looks a bit like a funnel. This will pull down the edge of the circle. The closer the zero is to the edge, the more the edge will get pulled down.
If you were able to unwrap the edge of the circle, keeping its vertical shape, you would have a picture of the frequency response.
MAKE A 3-D PLOT OF THIS IN MATHEMATICA TO ILLUSTRATE THIS POINT.
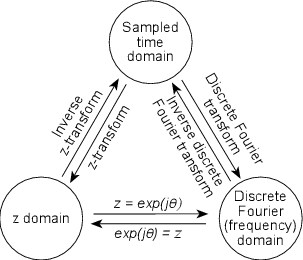
So far we have looked at how to calculate the frequency response (therefore the magnitude and phase responses) of a digital filter using zeros in the z-plane. However, you may have noticed that we have only discussed FIR filters in this section. We have not looked at what happens when you introduce feedback, therefore creating an IIR filter.
So, let’s make a simple IIR filter with a single delayed feedback with gain as is shown in Figure 9.131.
The equation for this filter is
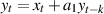 | (9.136) |
Notice now that the output is the sum of the input (the xt) and a gain-modified version (using the gain a1) of the output yt with a delay of k samples.
We already know from the previous section how to write this equation symbolically using operators (think back to the Johnny Cash example) as is shown in the equation below.
 | (9.137) |
Let’s do a little standard high-school algebra on this equation...
![Y = X +a1z-kY (9.138)
Y - a z-kY = X (9.139)
1 -k
X = Y[ - a1z Y] (9.140)
X = 1- a1z-k Y (9.141)](intro_to_sound_recording989x.png)
So, in a weird way, we can think of this IIR filter that relies on feedback as a FIR filter that only contains feedforward, except that we have to think of the filter backwards. The input, X is simply the output of the filter, Y , minus a delayed, gain-varied version of the output. This can be seen intuitively if you compare Figure 9.115 with Figure 9.131. You’ll notice that, if you look at one of the diagrams backwards (following the signal path from right to left), they’re identical.
Let’s continue with the algebra, picking up where we left off...
![[ -k]
X = 1 - a1z Y (9.142)
X
-------k = Y (9.143)
1- a1z
Y = ----X--- (9.144)
1 - a1z- k
---1----
Y = X 1- a1z-k (9.145)](intro_to_sound_recording990x.png)
Therefore, we can see right away that the transfer function of this IIR filter is
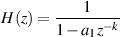 | (9.146) |
because that’s what gets multiplied by the input to get the output.
This, in turn, means that the magnitude response of the filter is
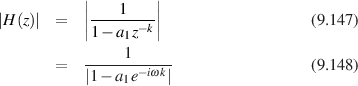
This raises an interesting problem. What happens if we make the denominator equal to 0? First of all, let’s find out what values make this happen.

Remember Euler’s identity which states that
 | (9.153) |
We therefore know that, for any value of ω and k, -1 ≤ e-jωk ≤ 1. In other words, a sinusoidal waveform just swings back and forth over time between -1 and 1.
We saw that the denominator of the equation for the magnitude response of our filter will be 0 when
 | (9.154) |
Therefore, the magnitude response of the filter will be 0 (at some values for ω and k) when a1 ≥ 1. THIS STATEMENT DOES NOT MAKE SENSE. FIX IT.
So what? Well, if the denominator in the equation describing the magnitude response of the filter goes to 0, then the magnitude response goes to ∞. Therefore, no matter what the input of the filter (other than an input of 0), the output will be ∞. This is bad because an infinite output signal is very, very loud... An intuitive way to think of this is that the filter goes nuts if the feedback causes it to get louder and louder over time. In the case of a single feedback delay, this is easy to think of, since it’s just a question of whether the gain applied to that delay outputs a bigger result than the input, which is fed into the delay again and made bigger and bigger and so on. In the case of a complicated filter lots of feedback and feedforward paths (and therefore lots of poles and zeros) you’ll have to do some math to figure out what will make the filter get out of control.
We saw that, if the numerator of the magnitude response equation of the filter goes to 0, then we put a zero in the z-plane plot of the response. Similarly, if the denominator of the equation goes to 0, then we put a pole on the z-plane plot of the response. Whereas a zero can be thought of as a deep “dent” in the 3D plot of the z-plane, a pole is a very high pointy tent-like shape coming up off the z-plane. This is shown in Figures 9.132.
Notice in Figure 9.132 that I have marked the pole using an “X” and placed it where
z-k = a1 This may seem odd, since we said a couple of equations ago that the
magic number is where  = z-k. I agree – it is a little odd, but just trust me for
now. We put the pole on the plot where z-k = the bottom half of the equation
(in this case, a1) and we’ll see in a couple of paragraphs how it ties back to
= z-k. I agree – it is a little odd, but just trust me for
now. We put the pole on the plot where z-k = the bottom half of the equation
(in this case, a1) and we’ll see in a couple of paragraphs how it ties back to
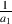 .
.
As we saw before, one way to intuitively think of the result of a pole on the magnitude response of the filter is to unwrap the edge of the circle and see how the pole pulls up the edge. This will give you an idea of where the total gain of the filter is higher than 1 relative to frequency.
Alternately, we can think of the magnitude response, again using the distance from
the pole’s location to the edge of the circle in the z-plane. However, there is a difference
in the way we think of this when compared with the zeros. In the case of the
zeros, the magnitude response at a given frequency was simply the distance
between the zero and the edge of the circle as we saw in Figures 9.128 and
9.129. We also saw that, if you have more than one zero, you multiply their
distances (to the location of a single frequency on the circle) together to get the
total gain of the filter for that frequency. The same is almost true for poles,
however you divide the distance instead of multiplying. So, in the case of a filter
with only one pole, you divide 1 by the distance from the pole’s location to
a frequency on the circle to get the gain of the filter at that frequency. This
is shown in Figures 9.133 and 9.134. (See, I told you that I’d link it back to
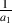 ...)
...)
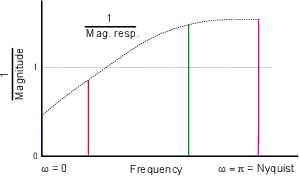
 . Note that this plot
is only roughly to scale – it is not terribly accurate.
. Note that this plot
is only roughly to scale – it is not terribly accurate.

TEXT AND GRAPHS TO EXPLAIN THE FOLLOWING Z-PLANE PLOTS
NOTES TO SELF:
MAGNITUDE
Poles, Magnitude = 1/D
Zeros, Magnitude = D
PHASE
Poles, Clockwise rotation, add the phase angle
Zeros, Clockwise rotation, subtract the phase angle
WHAT IF THERE ARE TWO OR MORE POLES OR ZEROS?
Poles, Magnitude = 1/D1 * 1/D2
Zeros, Mag = D1 * D2
Phase same as with single Pole or Zero
Since the application of digital signal processing to audio signals, there have been many attempts to create an impression of space using various algorithms. For the past 40 years, numerous researchers and commercial developers have devised multiple strategies for synthesizing virtual acoustic environments with varying degrees of success. Different methods have proven to be more suited to particular applications which can be divided into two major fields:
In the former case, synthetic reverberation is typically used to mimic real acoustic environments, generally with the intention of deceiving listeners into believing it is an actual space. In the latter case, the synthetic environments are generally intended to appear to be exactly that – synthetic – acoustics which are physically impossible in the real world, essentially resulting in the processing being used more as an instrument than an environment. In either instance, the reverberation must be aesthetically acceptable in order to enhance and complement rather than detract from the performance it accompanies.
Unfortunately, as is pointed out by Gardner [Gardner, 1992a], since a large part of the development of synthetic reverberation algorithms has been carried out by corporate concerns for commercial products, many secrets regarding their algorithms are not shared. Companies that rely on the sale of such products maintain superior product quality by ensuring that their procedures are not used by competitors, thus knowledge is hoarded rather than distributed, consequently slowing progress in the field. As a result, many specifics regarding current commercially-developed algorithms can only be either surmised or reverse-engineered.
Various algorithms and approaches to acoustics simulation have been developed since the advent of digital signal processing in the audio and film industries. These can be loosely organized into three groups based on their basic procedural characteristics:
Most modern digital reverberation engines use a collection of multitap delays, recursive comb filters and allpass filters connected in series and parallel with various combinations of parameter configurations to generate artificial acoustic spaces. Since these systems are based on assemblies of simple tapped delays with feedback and gain control they fall under the general term of tapped recirculating delay or TRD models [Roads, 1994]. This has been the standard method of generating artificial reverberation for approximately 40 years.
The first widely accepted method of creating synthetic reverberation using digital signal processing is attributed to Manfred R. Schroeder who, in 1961 and 1962, published two seminal papers describing procedures using simple series and parallel arrangements of recursive comb and allpass filters labelled “unit reverberators” [Schroeder, 1961][Schroeder, 1962] (see Figure 9.145) Despite the fact that these models used hours of computation time on mainframe computers, they remained the algorithms of choice and were used extensively at centres such as Stanford University and IRCAM for over a decade [Moorer, 1979].
In 1970 Schroeder suggested an improvement to his system with the inclusion of early power in the form of discrete reflections which will be discussed in the subsequent section [Schroeder, 1970]. While the Schroeder algorithms were universally accepted they do exhibit a number of problems outlined in 1979 by James Moorer. These complaints centre around the lack of perceptual transparency of the system, primarily a result of the excessive simplicity of the unit reverberators. Moorer specifies three major problems with the system [Moorer, 1979].
Moorer [Moorer, 1979] suggested a number of improvements on Schroeder’s original algorithm including the introduction of two new unit reverberators, termed an “oscillatory all-pass” and an “oscillatory comb,” and the use of low-pass filtering in the feedback loops both to smear the time response of discrete echoes and to simulate the absorption of high frequency signals in air for the reverberant field.
The TRD model relies heavily on the perceptual attributes of the unit reverberators in the attempt to mimic real acoustics. While the use of various combinations of recursive comb and allpass filters approximates the diffuse decay of a reverberant space, there is no effort to replicate precise characteristics of physical spaces. Although this system can be used to provide an adequate simulation of the later components in a reverberant decay, it can only be expected to provide a rough approximation for critical applications in spite of Schroeder’s claim in 1962 that the output from such a system, in some regards, was perceptually “indistinguishable” from recordings made in real spaces.
In 1970, the TRD system was improved dramatically with Schroeder’s inclusion of a multitap delay which provided simulated early reflections [Schroeder, 1970]. Over the past 30 years, this system has undergone numerous improvements, [Gardner, 1992b] [Christiansen, 1992] thanks largely to increases in complexity with increased processing power. Despite the fact that this model was the first system to be used to synthesize artificial acoustic environments, it remains the most commonly-used model in even the newest commercial devices. Its initial development relied on the efficiency of the TRD algorithms and the use of recursive elements to model reverberation perceptually. While this system does not provide an accurate representation of the real characteristics of a reverberant space, its efficiency and perceptual adequacy lie at the heart of its continued acceptance.
There are two principal methods used in calculating the real temporal and spatial characteristics of the reflection pattern of an enclosure, each providing advantages and disadvantages. These are the ray-trace model and the image model. Two additional methodologies are derived from these and are known as the cone trace model (also known as beam tracing) and the hybrid method.
Ray-trace model
Schroeder’s intention in the addition of a multitap delay to the TRD system was to simulate the early reflection pattern of a real enclosure. In order to determine the appropriate delay times, gains and panning for these delays, he chose to use a two-dimensional model of a real room, calculating the paths of 300 sound rays propagating outwards from the sound source towards the walls [Schroeder, 1970]. Assuming linear response characteristics both from the air and the reflective surface, he subsequently calculated a series of delays to simulate the early reflection patterns for a given source and listener location and specified room geometry. This delay cluster was then used to provide the early reflection pattern of the room, with the TRD model being used to provide the desired reverberant characteristics.
This is a simple example of the system which has come to be known as ray-tracing. In it, the expanding wavefront is considered as a number of rays of energy, typically equally spaced angularly around the sound source. As each ray propagates outwards, it will meet a reflecting surface and subsequently be re-directed into the enclosure at a new angle. This procedure continues until either a pre-determined limit on the order number of the reflection is reached or the ray encounters the receiver. The appropriate time and gain of each ray at the receiver is therefore calculated and stored, with the collection of all incoming rays resulting in the calculated impulse response of the room. In more sophisticated systems, the absorptive characteristics of each reflecting surface can be included by applying an appropriate filter to the impulse for each corresponding reflection.
This system is an excellent method for calculating the impulse response of a room with numerous surfaces with irregular geometry since the local interaction of each ray with the surrounding environment is considered throughout its entire propagation. Consequently, angular calculations are made in series and are therefore relatively simple. As a result it is the system most widely used in software developed for acoustics prediction [Dalenbäck et al., 1994]. One principal danger with this system is that, unless a large number of rays are used, it is possible that low-order reflections will be omitted since they will occur between angles. This is because the radiation patterns of sound sources are calculated on quantized angles instead of continuous space. Consequently, it is possible that the location of the receiver does not correspond to any of the emitted rays for some reflections.
Image model
While the ray trace model provides an excellent and efficient method of calculating the spatial and temporal locations of reflections in an enclosure with irregular geometry, it requires a very large number of calculated rays in order to assure that all early reflections are found. In cases where only the low-order reflections are required, the image model provides a more efficient method of calculation for specular reflective surfaces. In this model, the sound source is effectively duplicated to multiple locations outside the enclosure. These locations correspond to the virtual locations of sound sources which, in a free field, would result in the same delayed pressure wave as a perfect specular reflection. Figure 9.147 illustrates this concept. The figure on the left demonstrates the direct sound and first reflection using a simple ray trace model. In it, the reflection is calculated to occur at a particular location on the reflecting surface. In the figure on the right, the image model is used where the sound source is duplicated on the opposite side of the reflecting surface. The incoming pressure wave from this duplicated source exactly matches the pressure wave of the reflection in the diagram on the left.
This model was first proposed for the building of impulse responses of digitally synthesized acoustic environments in 1979 by Allen and Berkley [Allen and Berkley, 1979] however, the method was used by many other researchers previous to this to model specular reflective surfaces of a rectangular enclosure [Eyring, 1930] [Gibbs and Jones, 1972] [Berman, 1975]. In this paper, they suggested finding the total propagation delays of a reflection using this model, and subsequently rounding the delay to the nearest sample in the synthetic impulse response. This system could be repeated for any number of reflections with the resulting impulse response used as an FIR filter through which anechoic recordings would be convolved.
Peterson [Peterson, 1986] suggested an improvement to this system in the form of
interpolated delays. Whereas Allen and Berkley assumed that a maximum temporal
quantization error, caused by rounding off delay values, of  was tolerable, (where T s
is the sampling period) Peterson suggested that this corresponded to an unacceptable
interchannel phase error. This error can be eliminated by using interpolated rather than
quantized delay values.
was tolerable, (where T s
is the sampling period) Peterson suggested that this corresponded to an unacceptable
interchannel phase error. This error can be eliminated by using interpolated rather than
quantized delay values.
The advantages of the image model system lie in the efficiency of its method of calculation for specific reflections. The impulse responses of individual reflections are calculated as desired, and thus low-order reflections are provided by the system very quickly. The principal disadvantage of the system is its difficulty in processing irregular geometries, particularly for higher order reflections. Whereas the ray trace model computes the various reflections of a single ray in series, the image model does so in parallel – all reflections of a given ray must be known simultaneously in order to return a result [Borish, 1984]. Consequently, this model is used in systems where the enclosure is constructed of relatively simple shapes and only lower-order reflections are required.
Cone trace model
The cone trace method was developed in an attempt to maintain the simplicity of the ray trace model for higher-order reflections, while ensuring that lower-order reflections were not omitted due to quantization of the angular directions of the sound radiation. In this procedure, rather than using discrete rays emanating from the sound source at specific angles, a series of H overlapping cones are calculated with a gain function which is dependent on the relationship between the angular spread of the cone γo (derived using Equation 9.155) and the location of the receiver at angle γ. This gain, Gγ is calculated using Equation 9.156 [van Maercke, 1986].
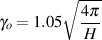 | (9.155) |
 | (9.156) |
Hybrid method
Another approach which combines the simplicity of the ray trace model with the accuracy of the image model is the hybrid method. This system is simply a combination of the two, using the image model for lower-order reflections and ray tracing for the higher orders [Vrlander, 1989].
While the ray-trace and image models use mathematical descriptions of real acoustic spaces, they do not necessarily mimic the behaviour of an acoustic wavefront in those spaces. This is due largely to the fact that each considers only the propagation speed and direction of the expanding wavefront, and does not take into account such factors as the diffusion or diffraction [Kleiner et al., 1993]. As a result, although these models will provide excellent models of early specular reflection patterns, they do not produce accurate impulse responses for high orders of reflections. This is because the spatial spread of quantized radiation angles increases with distance from the sound source, and thus the order of the reflection. Consequently, it is likely that many reflections will not be recorded at the receiver’s position. In order to achieve a higher level of accuracy, a model which is based on a larger set of physical rules is required. In this so-called physical model, the system is equipped with equations that describe the mechanical and acoustic behaviour of the various components of the physical system being modeled. In theory, the result is a system that mimics the behaviour of the physical counterpart [Roads, 1994].
The term “physical model” is widely-used in many fields to describe various systems. In music technology-based applications, a physical model is one where mathematical models of physical acoustics are used to produce the characteristics of a resonant instrument or enclosure [Roads, 1994]. This mathematical model can take various forms, however, the typical implementation involves a recursive delay including a filter in the feedback path, an example of which is the Karplus-Strong plucked string algorithm [Karplus and Strong, 1983].
Two general methods of physical models used in auralization and predictive acoustics software are known as the boundary element method (BEM), and the finite element method FEM.
Boundary element method
Using the boundary element method, surfaces are subdivided into discrete components, each with a particular set of reflective characteristics [Kleiner et al., 1993]. Each of these components is considered to be a sound source, re-radiating power into the enclosure with an individual contribution to the whole room impulse response.
One of the principal problems with the boundary element method is the large number of calculations required in order to build a complete impulse response. This is particularly true with higher order reflections, since the increase in the number of interacting elements is exponentially proportional to the order of reflection.
Finite element model
The boundary element method is limited in that it only considers the characteristics of the surfaces which define a space while neglecting the behaviour of elements within the space itself. The finite element model corrects for this omission, subdividing the entire room into a collection of interconnected discrete elements arranged in a mesh. In this manner, the entire space is modeled, albeit with a rather high computational cost. One notable example of the finite element method is the digital waveguide mesh.
Digital waveguide mesh
Various systems have been developed and proposed which use the concept of digital waveguides to simulate the resonant and reverberant characteristics both of room acoustics and, on a smaller scale, of instrument acoustics. Initially proposed for room models by Crawford in 1968 [Roads, 1994], digital waveguides use bidirectional delay lines (and therefore recursion) to simulate the characteristics of acoustic waveguides with considerable efficiency. A notable development in the field of room acoustics modeling was the extension of the digital waveguide into a multi-dimensional mesh. This mesh is comprised of a number of discrete digital waveguides that are interconnected using scattering junctions. In its canonical form, the delay time of the individual bidirectional delays is 1 sample. The purpose of the scattering junctions is to re-distribute the wave energy into connected delays based on the relative acoustic impedances of the incoming and outgoing waveguides. For example, in the case of a scattering junction in the centre of a room, the impedances of the outputs of all connected delays would be equal, therefore any incoming energy is equally distributed among all their inputs. By comparison, if the scattering junction is located at a very reflective surface, then there is a mismatch in the amplitudes of the waveforms that are routed to the connected delays, sending more power in some directions than others.
Typically, digital waveguide meshes are arranged in a two dimensional configuration as is represented in Figure 9.150. One excellent introductory description of this system is [Duyne and III, 1993].

There are a number of problems associated with the implementation of digital waveguide meshes such as dispersion and quantization error. One particular difficulty with using the discrete rather than a continuous representation of space that occurs in the mesh is frequency-dependent differences in wave propagation speed in different directions on the mesh. This is particularly noticeable in two-dimensional meshes with square layouts as shown in Figure 9.150. In such a configuration, diagonally-travelling waves have a frequency-independent propagation speed. Low-frequency waves travelling along either of the two axes will have an identical speed to their diagonal counterparts, however, high frequency information traveling along the axes has a speed of 0.707 that of lower frequencies. This results in a distortion of the wavefront in the form of a loss of transient information in some propagation directions.
One solution to this problem is to increase the number of dimensions on the mesh. Although the system is still used to model a two-dimensional surface, it contains a larger number of axes and thus reduces differences in wave speed with direction. One example of such a system is shown in Figure 9.151 which displays a triangular mesh. Savioja [Savioja, 1999] provides an evaluation of various mesh topologies and the resulting wave speeds.
Digital waveguide meshes also suffer from cumulative quantization errors due to the multiplicity of parallel and series combinations of gain modification in the junctions. One suggested solution to this issue is the re-distribution of the error into the spatial domain. In this topology, the quantization error is traded for a much less significant dispersion error on the mesh [Duyne and III, 1993].
Unfortunately, although physical modelling reverberation systems can produce excellent results, the processing power required to simulate the characteristics of large three-dimensional spaces is presently prohibitive in real-time systems.
In 1979, Moorer (1979) discussed the option of using a measurement of an existing space as a digital reverberator. In this system, an impulse response of a real room is measured and stored, and the characteristics of the measurement system are subtracted. This impulse response can subsequently be used as an FIR filter that can be convolved with an anechoic recording to produce a result equivalent to the recording reproduced in the space. More recently, it has become possible to implement such a system in real time as is exemplified by various hardware and software implementations.
There are two possible methodologies for performing the actual convolution known as real convolution and fast convolution. In the first, the impulse response is effectively treated as a multitap delay with a large number of taps (equal to the length of the impulse response in samples) and a gain control on each. Although this system can provide an output with extremely low latency, it typically requires an enormous amount of processing power. Consider for example, that in the case of a 2-second reverberant tail sampled at 44.1 kHz, a processing system using real convolution working in real time on a standard floating point processor with a large cache would be required to perform approximately 7.8 billion operations per second per channel.
Fast convolution relies on the interrelated properties of the frequency and time domains. Since the complex multiplication of two signals in the frequency domain is equivalent to the convolution of the same signals in the time domain, it is possible to perform an FFT on each signal simultaneously, multiply their respective real and imaginary components, and performing an inverse FFT on the product, producing a temporal convolution of the signals. This procedure results in a considerable savings in operations (844 million operations per second for the same configuration as the previous example with an FFT size of 2048 samples), however it does incur a number of issues to consider such as latencies caused by the FFT block size and strategies for dealing with overlapping results of the IFFT process.
There are two principal disadvantages of a convolution-based reverberator:
There is one overriding advantage in using this topology: sound quality. No artificial reverberation developed to date matches the realism of a system that uses correctly prepared measured impulse responses of real spaces.
In theory, a reverberant decay approaches a perfectly diffuse field; in fact, many linear acoustics texts assume that the reverberant tail is a diffuse field. While there are some indications that this may be overly simplified it can be used as an approximation. For example, in a TRD model, allpass and recursive comb filters are used to create a perceptual equivalent to a room’s reverberant tail. When a device is intended for a multichannel output, manufacturers typically alter the parameters of these filters in order to achieve the required number of uncorrelated, but perceptually similar signals in an effort to simulate this theoretical diffuse field.
In 1998, Rubak and Johansen suggested that an impulse response of this field could be simulated using a recursive pseudo-random algorithm with an applied decay envelope. According to preliminary listening tests, they reported that a pseudo-random reverberator could produce high-quality reverberation with a minimum echo density of 2000 per second and a repetition rate of no greater than 10 Hz [Rubak and Johansen, 1998][Rubak and Johansen, 1999].
Informal experiments prove that this method does indeed produce good results, however an extension on this model is recommended. A more realistic and controllable decay curve can be achieved by dividing the uncorrelated noise samples into constituent frequency bands and applying a different exponential decay envelope to each, typically using shorter times for higher frequency bands.
One excellent characteristic of this algorithm is the automatic decorrelation of the various output channels when different original noise samples are used. This contrasts with the sometimes painstaking attention to the parameter relationships required to achieve the same isolated result with unit reverberators. It should be noted, however, that although this system provides results equalling or possibly improving on the TRD model, it is considerably more computationally expensive and therefore unattractive as a useful procedure.