This week’s weird FFT

This week, I was testing a device that required that I look WAY down into the floor caused by the noise+distortion artefacts in the presence of a signal.

One trick to do this is to play a sinusoidal wave through the system and do an FFT of the output. However, as I described in this posting a long time ago, there is an interaction between the frequency you choose and the behaviour of an FFT on a digital signal (yes… I know it’s really a DFT – but let’s not be pedantic…)

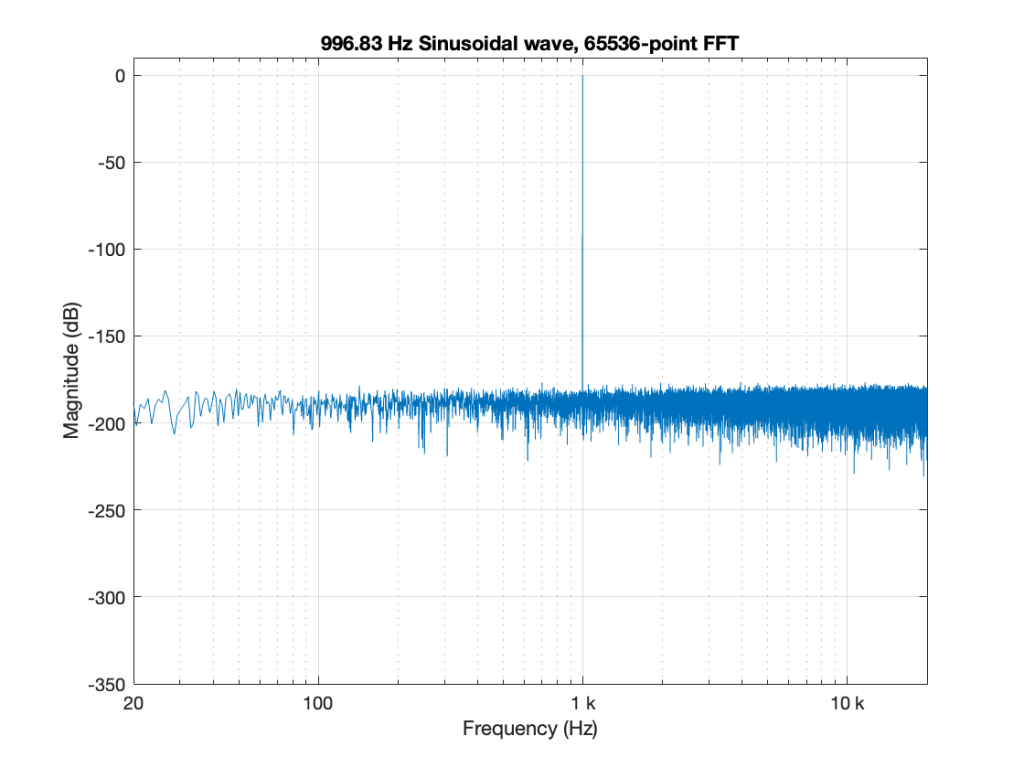
For example, if I do a 65536-point FFT on a 997 Hz sine tone in a 48 kHz sampling rate (with all the floating point precision I have available…) I get a magnitude response that looks like this:

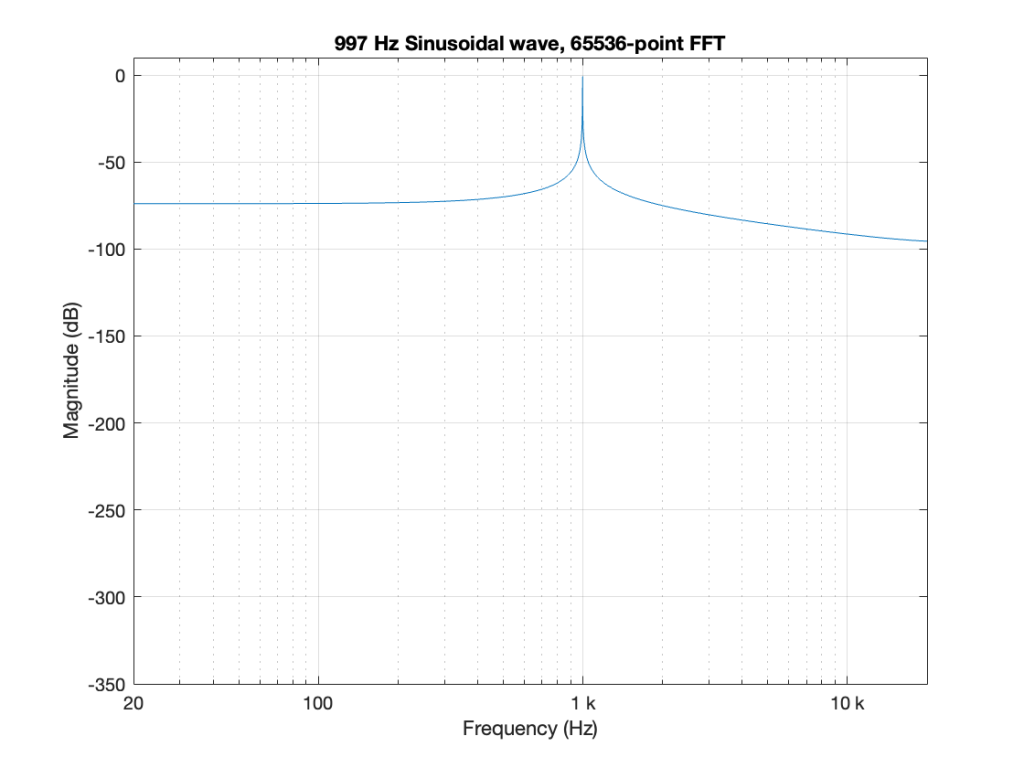
Figure 1. The magnitude response of a 997 Hz sine tone, but is it really?

Obviously, this is NOT the magnitude response of a sinusoidal wave. The “skirts” on either side of 997 Hz are artefacts caused by the fact that I’m using a rectangular window, and the sine wave’s last sample does not line up perfectly with its first when the FFT “wraps” it around to meet itself (read this leading up to Figure 10 for an explanation). That sharp discontinuity causes the extra energy in the other frequency bins as shown above.

If, however, I find out the frequency of the closest FFT bin, and make my sine wave THAT frequency instead, THEN I do an FFT and look at the magnitude response, it looks like Figure 2.

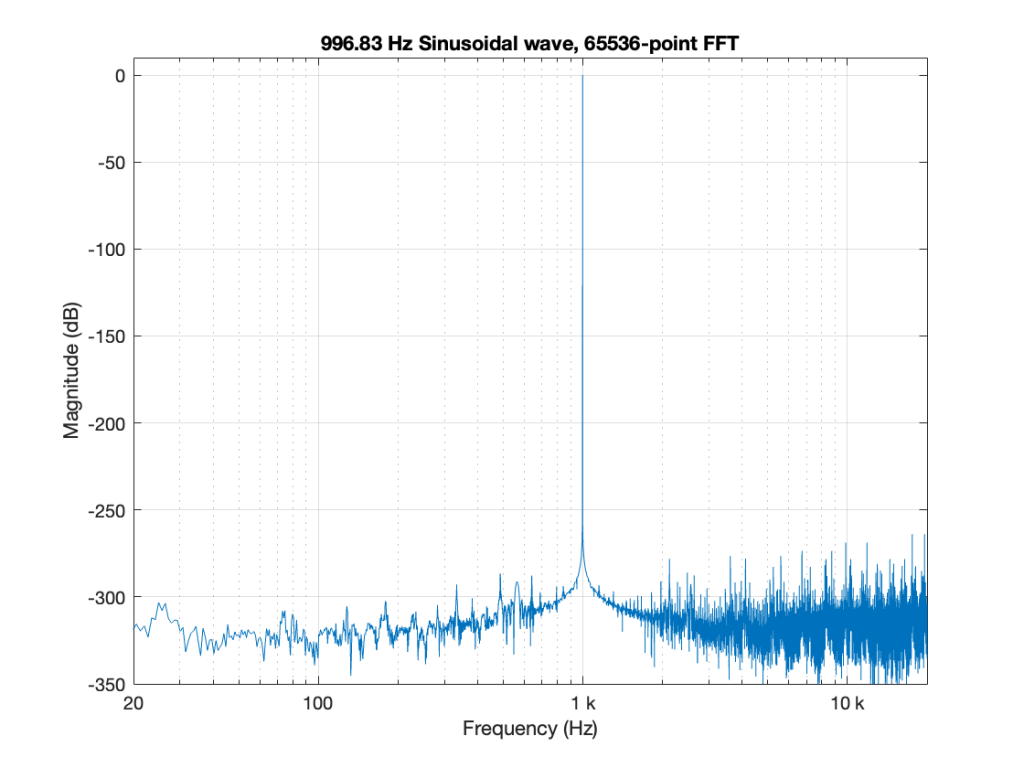
Figure 2. The magnitude response of a 996.8261718750000 Hz sine tone.

Notice that this is not a 997 Hz tone, but a 996.8261718750000 Hz tone instead.

Now the “noise floor” that you see there is the error in my sine wave caused by the precision of my calculator (Matlab). -300 dB is VERY low, and gives me plenty of room to see the errors in the thing that I might be testing (assuming that I can actually get that signal out to my Device Under Test or “DUT” and back in again from it).

Let’s say I were to represent the same sine wave using a 24-bit LPCM signal that has been correctly dithered with TPDF dither, and THEN I do the FFT and calculate the magnitude response. That would look like Figure 3.

Figure 3. The magnitude response of a 996.996.8261718750000 Hz sine tone that has been dithered and quantised with 24 bit precision.

Now, the energy at all the frequencies other than 996.8-ish Hz is the energy in the noise floor generated by the dither. (If you’re wondering why it’s almost 200 dB down, and not 141 dB down (6*24-3), it’s because the total energy in all those FFT bins add up to a noise floor that’s 141 dB below the sine tone.)

Okay. All of those plots show things that I’ve seen before – and are things that I would expect to see when measuring a device.

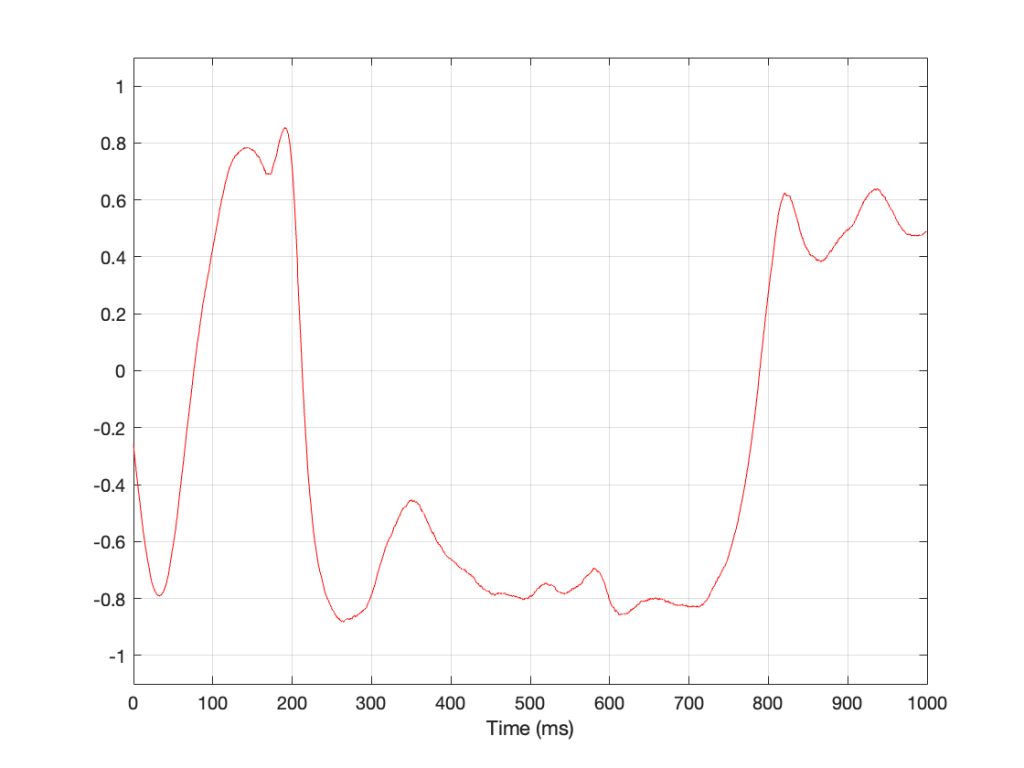
But then, this week, I did a measurement that produced the magnitude response shown in Figure 4.

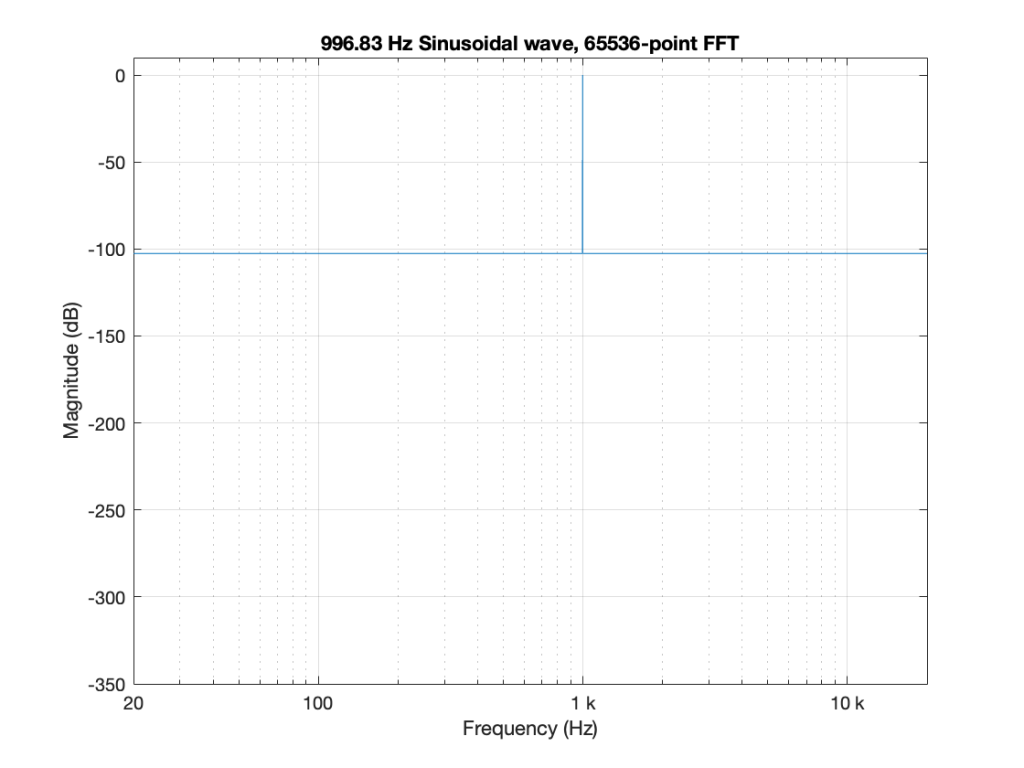
Figure 4. A 996.996.8261718750000 Hz sine tone and something else…

This is NOT something I’ve seen before, so it raised one of my two eyebrows. In retrospect, I should have known what would cause this, but at the time, I was very confused. It’s not a noise floor because it’s too flat. It’s not distortion because it doesn’t have harmonics. So what is it?

The answer is actually really simple.

The sine tone is visible as the spike in the magnitude plot, just like in all the others.
The flat horizontal line is the result of a single-sample click that happened sometime in the 65536 samples that I used to do the FFT.

The sum (or mix) of the sine + click results in the magnitude response plot you see above. If you’re looking at the signal itself, it just means that one of the 65536 samples has an error, and isn’t sitting on the sine curve. I’ve shown an example of this in Figure 5.

Figure 5. The sample with the error is shown in red. All other 65535 samples are behaving as they should

The greater the error of that one sample value, the higher the floor in Figure 4.

Of course, for these plots, I simulated everything in Matlab. However, the actual result was even more interesting / confusing, since the DUT didn’t have a flat magnitude response. So, instead of a nice, horizontal line like the one I’ve shown in Figure 4, I could see something like the response of the system as well, but I’ll stay away from the details of that to keep things simple here.

Tracking a drifting clock

Every once-in-a-while, I have to measure a system to find out whether its clock is behaving, or at the very least, whether its latency is stable over time. There are a number of different ways to do this, but I was trying to find a way that would be quick to implement and simple to analyse, if only as an initial “smoke test” to determine whether the system is working perfectly (which never happens) or which measurements we have to do next in order to figure out what exactly is going on.

Anyone who works in an engineering-type of area knows that the job doesn’t stop when you go home for the day. It percolates in the back of your head until, while you’re distracted by something else, the answer you’ve been looking for bubbles up to the frontal lobe. So, one evening I’m walking the dog in the forest, in the rain, and, like most people do, I was thinking about why we use 997 Hz sine tones to measure digital audio systems (if you don’t know the answer to this, check this posting). And that’s where it hit me. If we use a weird number to try and hit as many quantisation values as possible, what happens if we do the opposite?

Here’s a plot of a 4800 Hz sine tone, sampled at 48 kHz.

Figure 1: A 4.8 kHz sine tone sampled at 48 kHz.

This is the way we normally plot a digital audio signal, but it’s not really fair. What I’m doing there is to connect the sample values. However, when this signal is sent out of a DAC, it will be smoothed by a reconstruction filter so those sharp corners will disappear on their way out to the real world. However, for the purposes of this posting, this doesn’t matter, since what I’m really interested in are the sample values themselves, as shown in Figure 2.

Figure 2: The same signal plotted in Figure 1, showing the individual sample values.

You may notice something curious about this plot. Since I’ve chosen to plot a sine wave whose frequency is exactly 1/10th of the sampling rate, then each period of the waveform is 10 samples long, and the next period is identical to the previous one. This can be shown by connecting every 10th sample as shown in Figure 3.

Figure 3. When Fc = Fs/10, every 10th sample is identical.

Again a reminder: this is the reason we use the “weird” frequency of 997 Hz to test a digital audio system running at 44.1 kHz or 48 kHz.

In this case, testing a 48 kHz system with a 4.8 kHz tone can measure 10 sample values at most. (If I had chosen to start with a different phase, it might have been fewer sample values, since I would have gotten repetitions within a period.)

If I “connect the dots” for all 10 sample values, it will look like Figure 4.

Figure 4. Connecting all 10 sample values, similar to what was shown in Figure 3.

If I then do that for a much longer time window, it will look basically the same; I just won’t be able to see when the lines start and stop because we’ve zoomed out.

Figure 5. The same plot as Figure 4, but for a full second instead of showing only 1 ms.

What will happen to this plot if the clock is drifting? For example, if you’re playing a 4.8 kHz tone through a system that is NOT running at 48 kHz (even though it should), then the samples won’t appear at the right time, and so they will have a different instantaneous amplitude. In other words, a change in time will result in a change in phase, which will show up in a plot like the one in Figure 5 as a change in amplitude.

Let’s pretend that we set up a system like the one shown above, and let’s say that the signal that we record over there on the right hand side produces a plot like the one shown below in Figure 7.

Figure 7. The results of a hypothetical recording made in the test setup shown in Figure 6.

What does Figure 7 show us? Since the recording that we made with the sound card is at exactly 48 kHz, and since these are not horizontal lines, then this means that the recorded signal is not exactly 4.8 kHz.

However, this does not necessarily mean that the source (on the left side of Figure 6) is not transmitting a 4.8 kHz sine tone. It could mean that the clock that is determining the sampling rate in the loudspeaker is incorrect. So, the source “thinks” it’s playing a 4.8 kHz tone, but the loudspeaker is deciding otherwise for some reason. (This is a very normal behaviour. Nothing is perfect, and a Bluetooth speaker is a likely suspect for a number of errors…)

The curves in Figure 7 are sinusoidal. This means that the drift is constant. In other words, the sampling rate is wrong, but not varying, resulting in the wrong frequency of sine wave being played – but at least the frequency is not modulating. We can also see that each of the 10 sinusoidal waves makes about 1 cycle in the 1000 ms of the plot. This means that the clock is drifting by 1 period of the audio sine wave (4.8 kHz) ever 1000 ms. In other words, this is a system that it actually running at either 47990 Hz or 48010 Hz instead of 48000 Hz (because we’re either gaining or losing 10 samples every second). Unfortunately, without a little more attention, we don’t even know whether we’re running too slowly or too fast…

If the playback system’s clock (which controls its sampling rate) is not just incorrect but unstable, then you might see something like Figure 8, where I’ve only connected one of the 10 samples values.

Figure 8. The results of connecting every 10th sample of what should be a 4.8 kHz sine wave being played by a system with a drifting clock. Yes, this is a “real” system. Yes, it’s behaving very badly…

If I were to plot the same slice of time, showing all 10 samples in the sine wave, they would look like Figure 9. Admittedly, this is probably less useful than Figure 8.

Figure 9. The same data shown in Figure 8, but plotting all 10 samples of the 4.8 kHz period.

Obviously, this doesn’t tell us what’s going on other than to say that it’s obvious that this system is NOT behaving. However, we can get a little useful information. For example, we can see that the clock drift is modulating more from 0 ms to 200 ms, and then settles down to a more stable (and more correct) value from 200 to about 600 ms.

It would take more analysis to learn enough about this system to know what’s happening. However, as a smoke test to let you know whether it’s behaving well enough to not worry too much, or to see where you need to “zoom in” to find out more information.

Dynamic Styli Correlator Pt. 5

In the last posting, I showed a scale drawing of a 15 µm radius needle on a 1 kHz sine tone with a modulation velocity of 50 mm/s (peak) on the inside groove of a record. Looking at this, we could see that the maximum angular rotation of the contact point was about 13º away from vertical, so the total range of angular rotation of that point would be about 27º.

I also mentioned that, because vinyl is mastered so that the signal on the groove wall has a constant velocity from about 1 kHz and upwards, then that range will not change for that frequency band. Below 1 kHz, because the mastering is typically ensuring a constant amplitude on the groove wall, then the range decreases with frequency.

We can do the math to find out exactly what the angular rotation the contact point is for a given modulation velocity and groove speed.

Figure 1: A scale drawing of a 15 µm radius needle on a 1 kHz sine tone with a modulation velocity of 50 mm/s (peak) on the inside groove of a record. These two points are the two extremes of the angular rotation of the contact point.

Looking at Figure 1, the rotation is ±13.4º away from vertical on the maximum; so the total range is 26.8º. We convert this to a time modulation by converting that angular range to a distance, and dividing by the groove speed at the location of the needle on the record.

If we repeat that procedure for a range of needle radii from 0 µm to 75 µm for the best-case (the outside groove) and the worst-case (the inside groove), we get the results shown in Figure 2.

Figure 2. The peak-to-peak equivalent “jitter” values of the inside and outside grooves for a range of needle radii.

Dynamic Styli Correlator Pt. 4

Back in Part II of what is turning out to be a series of postings on this topic, I wrote

If this were a digital system instead of an analogue one, we would be describing this as ‘signal-dependent jitter’, since it is a time modulation that is dependent on the slope of the signal. So, when someone complains about jitter as being one of the problems with digital audio, you can remind them that vinyl also suffers from the same basic problem…

As I was walking the dog on another night, I got to thinking whether it would be possible to compare this time distortion to the jitter specifications of a digital audio device. In other words, is it possible to use the same numbers to express both time distortions? That question led me here…

Remember that the effect we’re talking about is caused by the fact that the point of contact between the playback needle and the surface of the vinyl is moving, depending on the radius of the needle’s curvature and the slope of the groove wall modulation. Unless you buy a contact line needle, then you’ll see that the radius of its curvature is specified in µm – typically something between about 5 µm and 15 µm, depending on the pickup.

Now let’s do some math. The information and equations for these calculations can be found here.

We’ll start with a record that is spinning at 33 1/3 RPM. This means that it makes 0.556 revolutions per second.

The Groove Speed relative to the needle is dependent on the rotation speed and the radius – the distance from the centre of the record to the position of the needle. On a 12″ LP, the groove speed at the outside groove where the record starts is 509.8 mm/sec. At the inside groove at the end of the record, it’s 210.6 mm/sec.

Let’s assume that the angular rotation of the contact point (shown in Figure 1) is 90º. This is not based on any sense of scale – I just picked a nice number.

Figure 1. Artists rendition of the range of the point of contact between the surface of the vinyl and the pickup needle.

We can convert that angular shift into a shift in distance on the surface of the vinyl by finding the distance between the two points on the surface, as shown below in Figure 2. Since you might want to choose an angular rotation that is not 90º, you can do this with the following equation:

2 * sin(AngularRotation / 2) * radius

So, for example, for a needle with a radius of 10 µm and a total angular rotation of 90º, the distance will be:

2 * sin(90/2) * 10 = 14.1 µm

Figure 2. The angular range from Figure 1 converted to a linear distance on the vinyl’s surface.

We can then convert the “jitter” as a distance to a jitter in time by dividing it by the distance travelled by the needle each second – the groove speed in µm per second. Since that groove speed is dependent on where the needle is on the record, we’ll calculate it as best-case and a worst-case values: at the outside and the inside of the record.

Jitter Distance / Groove Speed = Jitter in time

For example, at the inside of the record where the jitter is worst (because the wavelength is shortest and therefore the maximum slope is highest), the groove speed is about 210.6 mm/sec or 210600 µm/sec.

Then the question is “what kind of jitter distance should we really expect?”

Figure 3. Scale drawing of a needle on a record.

Looking at Figure 3 which shows a scale drawing of a 15 µm radius needle on a 1 kHz tone with a modulation velocity of 50 mm/s (peak) on the inside groove of a record, we can see that the angular rotation at the highest (negative) slope is about 13.4º. This makes the total range about 27º, and therefore the jitter distance is about 7.0 µm.

If we have a 27º angular rotation on a 15 µm radius needle, then the jitter will be

7.0 / 210600 = 0.0000332 or 33.2 µsec peak-to-peak

Of course, as the radius of the needle decreases, the angular rotation also decreases, and therefore the amount of “jitter” drops. When the radius = 0, then the jitter = 0.

It’s also important to note that the jitter will be less at the outside groove of the record, since the wavelength is longer, and therefore the slope of the groove is lower, which also reduces the angular rotation of the contact point.

Since the groove on records are typically equalised to ensure that you have a (roughly) constant velocity above 1 kHz and a constant amplitude below, then this means that the maximum slope of the signal and therefore the range of angular rotation of the contact point will be (roughly) the same from 1 kHz to 20 kHz. As the frequency of the signal descended from 1 kHz and downwards, the amplitude remains (roughly) the same, so the velocity decreases, and therefore the range of the angular rotation of the contact point does as well.

In other words, the amount of jitter is 0 at 0 Hz, and increases with frequency until about 1 kHz, then it remains the same up to 20 kHz.

As one final thing: as I was drawing Figure 3, I also did a scale drawing of a 20 kHz signal with the same 50 mm/s modulation velocity and the same 15 µm radius needle. It’s shown in Figure 4.

Figure 4. Scale drawing of a needle on a record.

As you can see there, the needle’s 15 µm radius means that it can’t drop into the trough of the signal. So, that needle is far too big to play a CD-4 quad record (which can go all the way up to 45 kHz).

Internal vs. External Volume Control

#93 in a series of articles about the technology behind Bang & Olufsen

A question came to my desk this week from a customer who would like to connect a third-party streaming device to his Beolab 50s. He plans to use a USB-Audio connection and his question was “Should I control the volume of the audio signal in the streamer or in the Beolab 50s?” There are three different ways to configure these two options:

Control the volume in the streamer using its interface, and send a signal that has been volume-regulated to the Beolab 50s, which should then be set to have a start up default volume such that the maximum volume on the streamer results in a level that is as loud as the customer will ever want it to be. In order to do this, the Beolab 50s need to be set to ignore the volume information that is received on the USB-Audio connection.
Set the streamer to output an unregulated signal, and set the Beolab 50s to obey the volume information that is received on the USB-Audio connection, then use the streamer’s interface for the volume control (which would actually be happening inside the Beolab 50s).
Set the streamer to output an unregulated signal, and set the Beolab 50s to disobey the volume information that is received on the USB-Audio connection, then use the Beolab 50’s interface for the volume control (which would actually be happening inside the Beolab 50s).

Of course, one way to answer the question is “where do you want to control the volume?” For example, if it’s with a remote control for the Beolab 50s, then the answer is “use option #3”. If you’d prefer to use the streamer’s app, for example, then the answer is “use option #1 or #2”.

However, the question came to my desk because it was specifically about the technical performance of the audio signal. Which of these three options results in the highest audio “quality”? (I put the word “quality” in quotation marks because it is a loaded term, and might mean different things to different persons…)

The simplest answer without getting into any details is “it probably doesn’t matter“. However, that answer is based on a couple of assumptions that may or may not be wrong.

Hypothetically, the Beolab 50 can output an audio signal that peaks at about 122 dB SPL measured at 1 m in a free field, albeit not at all frequencies present at its output. (This is because there are some physical limitations of how far the woofers can move, which means that you can’t get 122 dB SPL at 20 Hz, for example.) The noise floor of the Beolab 50s is about 0 dB SPL measured in the same place (again, this is frequency-dependent). So, it has a total dynamic range at its output of about 122 dB.

The maximum output level is a result of a combination of the loudspeaker drivers, the amplifiers, and the power supply, however, these have all been chosen to reach their maximum outputs approximately simultaneously, so changing one of the three won’t make a big difference.

The noise floor is a result of the combination of the loudspeaker drivers’ sensitivities, the amplifiers’ noise floors, and the signal that feeds the amplifiers: the DAC outputs’ noise floors. For the purposes of this discussion, I’m sticking with a digital input, so we don’t need to worry about the noise floor of the ADC at the loudspeaker’s input.

If you have an audio signal at one of the digital inputs of the Beolab 50, and that signal is at its loudest possible level (for a sine wave, that’s 0 dB FS; or 0 dB relative to Full Scale). At Beolab 50’s maximum volume setting, this will produce a peak output level of 122 dB SPL (depending on the frequency as I mentioned above).

All digital inputs of the Beolab 50 accept at least a 24 bit word length. This means that the dynamic range of the digital input signal itself is about 6 * 24 – 3 = 141 dB. This in turn means that the hypothetical noise floor of a correctly-dithered 24-bit signal is 19 dB below the noise floor of the loudspeakers even at their maximum volume setting. (because 122 – 141 = -19)

In other words, if we assume that the streamer has a correctly-implemented gain function for its volume control, using TPDF dither implemented at the 24-bit level, then its noise floor will be 19 dB below the “natural” noise floor of the Beolab 50. Therefore, if the volume is controlled in the streamer, any artefacts will be masked by the 50s themselves.

On the other hand, the Beolab 50s volume control is done using a gain function that is performed in a 32-bit floating point calculation, which means that it has a dynamic range of 144 to 150 dB. (See this posting for an explanation and comparison of fixed point and floating point systems.) So the noise generated by the internal volume control will be somewhere between 22 and 26 dB below the “natural” noise floor of the Beolab 50.

So, (assuming my assumptions are correct) the noise floor that is produced by controlling the volume control in either the streamer or the Beolab 50s is FAR below the constant noise floor of the DAC / amplifiers.

In addition, the noise floors have roughly the same spectra (in other words, you don’t have pink noise in one case but white noise in the other; they’re all producing white noise). And since both are so far below, it really doesn’t matter. Arguing about whether the noise is 19 dB lower or 22 dB lower is a waste of good argument time, unless you paid for the four-and-a-half-hour argument instead of the five-minute one…

Important Notes

If the customer was asking about using the analogue input, then the answer MIGHT have been different.

Also, if my assumption about a 24-bit signal coming from the streamer, or that it has a correctly-implemented gain function for its volume control are incorrect, the this answer MIGHT be incorrect as well.

32 is a lot of bits…

Once upon a time, I did a blog posting about why, when we test digital audio systems, we typically use a 997 Hz sine wave instead of a 1000 Hz tone.

The short version of this is the following:

Let’s say that I digitally create a (not-dithered) 1000 Hz sine wave at 0 dB FS in a 16-bit system running at 48 kHz. This means that every second, there are exactly 1000 cycles of the wave, and since there are 48,000 samples per second, this, in turn means that there is one cycle every 48 samples, so sample #49 is identical to sample #1.

So, we are only testing 48 of the possible 2^16 ( = 65,536) quantisation values, right?

Wrong. It’s worse than you think.

If we zoom in a little more, we can see that Sample #1 = 0 (because it’s a sine wave). Sample #25 is also equal to 0 (because 48,000 / 1,000 is a nice number that is divisible by 2).

Unfortunately, 48,000 / 1,000 is a nice number that is also divisible by 4. So what? This means that when the sine wave goes up from 0 to maximum, it hits exactly the same quantisation values as it does on the way from maximum back down to 0. For example, in the figure below, the values of the two samples shown in red are identical. This is true for all symmetrical points in the positive side and the negative side of the wave.

Jumping ahead, this means that, if we make a “perfect” 1 kHz sine wave at 48 kHz (regardless of how many bits in the system) we only test a total of 25 quantisation steps. 0, 12 positive steps, and 12 negative ones.

Not much of a test – we only hit 25 out of a possible 65,546 values in a 16-bit system (or 25 out of 16,777,216 possible values in a 24-bit system).

What if I wanted to make a signal that tested ALL possible quantisation values in an LPCM system? One way to do this is to simply make a linear ramp that goes from the lowest possible value up to the highest possible value, step by step, sample by sample. (of course, there are other ways, but it doesn’t matter… we’re just trying to hit every possible quantisation value…)

How long would it take to play that test signal?

First we convert the number of bits to the number of quantisation steps. This is done using the equation 2^bits. So, you get the following results

Number of Bits	Number of Quantisation Steps
16	65,536
24	16,777,216
32	4,294,967,296

If the value of each sample has a different quantisation value, and we play the file at the sampling rate then we can calculate the time it will take by dividing the number of quantisation steps by the sampling rate. This results in the following:

Sampling Rate (kHz)	16 Bits	24 Bits	32 Bits
44.1	1.5 seconds	6.4 minutes	27.1 hours
48	1.4 seconds	5.8 minutes	24.9 hours
88.2	0.7 seconds	3.2 minutes	13.5 hours
96	0.7 seconds	2.9 minutes	12.4 hours
176.4	0.4 seconds	1.6 minutes	6.8 hours
192	0.3 seconds	1.5 minutes	6.2 hours
352.8	0.2 seconds	47.6 seconds	3.4 hours
384	0.2 seconds	43.7 seconds	3.1 hours
705.6	0.1 seconds	23.8 seconds	1.7 hours
768	0.1 seconds	21.8 seconds	1.6 hours

So, the moral of the story is, if you’re testing the validity of a quantiser in a 32-bit fixed-point system, and you’re not able to do it off-line (meaning that you’re locked to a clock running at the correct sampling rate) you’d either (1) hope that it’s also a crazy-high sampling rate or (2) that you’re getting paid by the hour.

Why I am thinking about this?

I often get asked for my opinion about audio players; these days, network streamers especially, since they’re in style.

Let’s say, for example, that someone asked me to recommend a network streamer for use with their system. In order to recommend this, I need to measure it to make sure it behaves.

One of the tests I’m going to run is to ensure that every sample value on a file is accurately output from the device. Let’s also make it simple and say that the device has a digital output, and I only need to test 3 LPCM audio file formats (WAV, AIFF and FLAC – since those can be relied to give a bit-for-bit match from file to output). (We’ll also pretend that the digital output can support a 32-bit audio word…)

So, to run this test, I’m going to

create test files that I described above (checking every quantisation value at all three bit depths and all 10 sampling rates)
play them
record them
and then compare whether I have a bit-for-bit match from input (the original file) to the output

If you add up all the values in the table above for the 10 sampling rates and the three bit depths, then you get to a total of 4.2 DAYS of play time (playing audio constantly 24 hours a day) per file format.

So, say I wanted to test three file formats for all of the sampling rates and bit depths, then I’m looking at playing & recording 12.6 days of audio – and then I can start the analysis.

REALLY‽

Of course this is silly… I’m not going to test a 32-bit, 44.1 kHz file… In fact, if I don’t bother with the 32-bit values at all, then my time per file format drops from 4.2 days down to 23.7 minutes of play time, which is a lot more feasible, but less interesting if I’m getting paid by the hour.

However, it was fun to calculate – and it just goes to show how big a number 2^32 is…

What is a “virtual” loudspeaker? Part 3

#91.3 in a series of articles about the technology behind Bang & Olufsen

In Part 1 of this series, I talked about how a binaural audio signal can (hypothetically, with HRTFs that match your personal ones) be used to simulate the sound of a source (like a loudspeaker, for example) in space. However, to work, you have to make sure that the left and right ears get completely isolated signals (using earphones, for example).

In Part 2, I showed how, with enough processing power, a large amount of luck (using HRTFs that match your personal ones PLUS the promise that you’re in exactly the correct location), and a room that has no walls, floor or ceiling, you can get a pair of loudspeakers to behave like a pair of headphones using crosstalk cancellation.

There’s not much left to do to create a virtual loudspeaker. All we need to do is to:

Take the signal that should be sent to a right surround loudspeaker (for example) and filter it using the HRTFs that correspond to a sound source in the location that this loudspeaker would be in. REMEMBER that this signal has to get to your two ears since you would have used your two ears to hear an actual loudspeaker in that location.
Send those two signals through a crosstalk cancellation processing system that causes your two loudspeakers to behave more like a pair of headphones.

Figure 1: A block diagram of the system described above.

One nice thing about this system is that the crosstalk cancellation is only there to ensure that the actual loudspeakers behave more like headphones. So, if you want to create more virtual channels, you don’t need to duplicate the crosstalk cancellation processor. You only need to create the binaurally-processed versions of each input signal and mix those together before sending the total result to the crosstalk cancellation processor, as shown below.

Figure 2: You only need one crosstalk cancellation system for any number of virtual channels.

This is good because it saves on processing power.

So, there are some important things to realise after having read this series:

All “virtual” loudspeakers’ signals are actually produced by the left and right loudspeakers in the system. In the case of the Beosound Theatre, these are the Left and Right Front-firing outputs.
Any single virtual loudspeaker (for example, the Left Surround) requires BOTH output channels to produce sound.
If the delays (aka Speaker Distance) and gains (aka Speaker Levels) of the REAL outputs are incorrect at the listening position, then the crosstalk cancellation will not work and the virtual loudspeaker simulation system won’t work. How badly is doesn’t work depends on how wrong the delays and gains are.
The virtual loudspeaker effect will be experienced differently by different persons because it’s depending on how closely your actual personal HRTFs match those predicted in the processor. So, don’t get into fights with your friends on the sofa about where you hear the helicopter…
The listening room’s acoustical behaviour will also have an effect on the crosstalk cancellation. For example, strong early reflections will “infect” the signals at the listening position and may/will cause the cancellation to not work as well. So, the results will vary not only with changes in rooms but also speaker locations.

Finally, it’s worth nothing that, in the specific case of the Beosound Theatre, by setting the Speaker Distances and Speaker Levels for the Left and Right Front-firing outputs for your listening position, then you have automatically calibrated the virtual outputs. This is because the Speaker Distances and Speaker Levels are compensations for the ACTUAL outputs of the system, which are the ones producing the signal that simulate the virtual loudspeakers. This is the reason why the four virtual loudspeakers do not have individual Speaker Distances and Speaker Levels. If they did, they would have to be identical to the Left and Right Front-firing outputs’ values.

What is a “virtual” loudspeaker? Part 2

#91.2 in a series of articles about the technology behind Bang & Olufsen

In Part 1, I talked at how a binaural recording is made, and I also mentioned that the spatial effects may or may not work well for you for a number of different reasons.

Let’s go back to the free field with a single “perfect” microphone to measure what’s happening, but this time, we’ll send sound out of two identical “perfect” loudspeakers. The distances from the loudspeakers to the microphone are identical. The only difference in this hypothetical world is that the two loudspeakers are in different positions (measuring as a rotational angle) as shown in Figure 1.

Figure 1: Two identical, “perfect” loudspeakers in a free field with a single “perfect” microphone.

In this example, because everything is perfect, and the space is a free field, then output of the microphone will be the sum of the outputs of the two loudspeakers. (In the same way that if your dog and your cat are both asking for dinner simultaneously, you’ll hear dog+cat and have to decide which is more annoying and therefore gets fed first…)

Figure 2: The output from the microphone is the sum of the outputs from the two loudspeakers. At any moment in time, the value of the top plot + the value of the middle plot = the value of the bottom plot.

IF the system is perfect as I described above, then we can play some tricks that could be useful. For example, since the output of the microphone is the sum of the outputs of the two loudspeakers, what happens if the output of one loudspeaker is identical to the other loudspeaker, but reversed in polarity?

Figure 3: If the output of Loudspeaker 1 is exactly the same as the output of Loudspeaker 2 except for polarity, then the sum (the output of the microphone) is always 0.

In this example, we’re manipulating the signals so that, when they add together, you nothing at the output. This is because, at any moment in time, the value of Loudspeaker 2’s output is the value of Loudspeaker 1’s output * -1. So, in other words, we’re just subtracting the signal from itself at the microphone and we get something called “perfect cancellation” because the two signals cancel each other at all times.

Of course, if anything changes, then this perfect cancellation won’t work. For example, if one of the loudspeakers moves a little farther away than the other, then the system is broken, as shown below.

Figure 4: A small shift in time in the output of Loudspeaker 2 cases the cancellation to stop working so well.

Again, everything that I’ve said above only works when everything is perfect, and the loudspeakers and the microphone are in a free field; so there are no reflections coming in and ruining everything.

We can now combine these two concepts:

using binaural signals to simulate a sound source in a location (although this would normally be done using playback over earphones to keep it simple) and
using signals from loudspeakers to cancel each other at some location in space as a

to create a system for making virtual loudspeakers.

Let’s suspend our adherence to reality and continue with this hypothetical world where everything works as we want… We’ll replace the microphone with a person and consider what happens. To start, let’s just think about the output of the left loudspeaker.

Figure 5: The output of the left loudspeaker reaches both ears with different time/frequency characteristics caused by the HRTF associated with that sound source location.

If we plot the impulse responses at the two ears (the “click” sound from the loudspeaker after it’s been modified by the HRTFs for that loudspeaker location), they’ll look like this:

Figure 6: The impulse responses of the HRTFs for a sound source at 30º left of centre.

What if were were able to send a signal out of the right loudspeaker so that it cancels the signal from the left loudspeaker at the location of the right eardrum?

Figure 7: What if we could cancel the signal from the left loudspeaker at the right ear using the right loudspeaker?

Unfortunately, this is not quite as easy as it sounds, since the HRTF of the right loudspeaker at the right ear is also in the picture, so we have to be a bit clever about this.

So, in order for this to work we:

Send a signal out of the left loudspeaker.
We know that this will get to the right eardrum after it’s been messed up by the HRTF. This is what we want to cancel…
…so we take that same signal, and
- filter it with the inverse of the HRTF of the right loudspeaker
  (to undo the effects of the HRTF of the right loudspeaker’s signal at the right ear)
- filter that with the HRTF of the left loudspeaker at the right ear
  (to match the filtering that’s done by your head and pinna)
- multiply by -1
  (so that it will cancel when everything comes together at your right eardrum)
- and send it out the right loudspeaker.

Hypothetically, that signal (from the right loudspeaker) will reach your right eardrum at the same time as the unprocessed signal from the left loudspeaker and the two will cancel each other, just like the simple example shown in Figure 3. This effect is called crosstalk cancellation, because we use the signal from one loudspeaker to cancel the sound from the other loudspeaker that crosses to the wrong side of your head.

This then means that we have started to build a system where the output of the left loudspeaker is heard ONLY in your left ear. Of course, it’s not perfect because that cancellation signal that I sent out of the right loudspeaker gets to the left ear a little later, so we have to cancel the cancellation signal using the left loudspeaker, and back and forth forever.

If, at the same time, we’re doing the same thing for the other channel, then we’ve built a system where you have the left loudspeaker’s signal in the left ear and the right loudspeaker’s signal in the right ear; just like a pair of headphones!

However, if you get any of these elements wrong, the system will start to under-perform. For example, if the HRTFs that I use to predict your HRTFs are incorrect, then it won’t work as well. Or, if things aren’t time-aligned correctly (because you moved) then the cancellation won’t work.

on to Part 3

What is a “virtual” loudspeaker? Part 1

#91.1 in a series of articles about the technology behind Bang & Olufsen

Without connecting external loudspeakers, Bang & Olufsen’s Beosound Theatre has a total of 11 independent outputs, each of which can be assigned any Speaker Role (or input channel). Four of these are called “virtual” loudspeakers – but what does this mean? There’s a brief explanation of this concept in the Technical Sound Guide for the Theatre (you’ll find the link at the bottom of this page), which I’ve duplicated in a previous posting. However, let’s dig into this concept a little more deeply.

To begin, let’s put a “perfect” loudspeaker in a free field. This means that it’s in a space that has no surfaces to reflect the sound – so it’s an acoustic field where the sound wave is free to travel outwards forever without hitting anything (or at least appear as this is the case). We’ll also put a “perfect” microphone in the same space.

Figure 1: A loudspeaker and a microphone (the circle) in a free field: an infinite space completely free of reflective surfaces.

We then send an impulse; a very short, very loud “click” to the loudspeaker. (Actually a perfect impulse is infinitely short and infinitely loud, but this is not only inadvisable but impossible, and probably illegal.)

Figure 2: The “click” signal that’s sent to the input of the loudspeaker.

That sound radiates outwards through the free field and reaches the microphone which converts the acoustic signal back to an electrical one so we can look at it.

Figure 3: The “click” signal that is received at the microphone’s location and sent out as an electrical signal.

There are three things to notice when you compare Figure 3 to Figure 2:

The signal’s level is lower. This is because the microphone is some distance from the loudspeaker.
The signal is later. This is because the microphone is some distance from the loudspeaker and sound waves travel pretty slowly.
The general shape of the signals are identical. This is because I said that the loudspeaker and the microphone were both “perfect” and we’re in a space that is completely free of reflections.

What happens if we take away the microphone and put you in the same place instead?

Figure 4: The microphone has been replaced by something more familiar.

If we now send the same click to the loudspeaker and look at the “outputs” of your two eardrums (the signals that are sent to your brain), these will look something like this:

Figure 5: The outputs of your two eardrums with the same “click” signal from the loudspeaker.

These two signals are obviously very different from the one that the microphone “hears” which should not be a surprise: ears aren’t microphones. However, there are some specific things of which we should take note:

The output of the left eardrum is lower than that of the right eardrum. This is largely because of an effect called “head shadowing” which is exactly what it sounds like. The sound is quieter in your left ear because your head is in the way.
The signal at the right eardrum is earlier than at the left eardrum. This is because the left eardrum is not only farther away, but the sound has to go around your head to get there.
The signal at the right eardrum is earlier than the output of the microphone output (in Figure 3) because it’s closer to the loudspeaker. (I put the microphone at the location of the centre of the simulated head.) Similarly the left ear output is later because it’s farther away.
The signal at the right eardrum is full of spikes. This is mostly caused by reflections off the pinna (the flappy thing on the side of your head that you call your “ear”) that arrive at slightly different times, and all add together to make a mess.
The signal at the left eardrum is “smoother”. This is because the head itself acts as a filter reducing the levels of the high frequency content, which tends to make things less “spiky”.
Both signals last longer in time. This is the effect of the ear canal (the “hole” in the side of your head that you should NOT stick a pencil in) resonating like a little organ pipe.

The difference between the signals in Figures 2 and 4 is a measurement of the effect that your head (including your shoulders, ears/pinnae) has on the transfer of the sound from the loudspeaker to your eardrums. Consequently, we geeks call it a “head-related transfer function” or HRTF. I’ve plotted this HRTF as a measurement of an impulse in time – but I could have converted it to a frequency response instead (which would include the changes in magnitude and phase for different frequencies).

Here’s the cool thing: If I put a pair of headphones on you and played those two signals in Figure 5 to your two ears, you might be able to convince yourself that you hear the click coming from the same place as where that loudspeaker is located.

Although this sounds magical, don’t get too excited right away. Unfortunately, as with most things in life, reality tends to get in the way for a number of reasons:

Your head and ears aren’t the same shape as anyone else’s. Your brain has lived with your head and your ears for a long time, and it’s learned to correlate your HRTFs with the locations of sound sources. If I suddenly feed you a signal that uses my HRTFs, then this trick may or may not work, depending on how similar we are. This is just like borrowing someone else’s glasses. If you have roughly the same prescription, then you can see. However, if the prescriptions are very different, you’ll get a headache very quickly.
In reality, you’re always moving. So, even if the sound source is not moving, the specific details of the HRTFs are always changing (because the relative positions and angles to your ears are changing) but my system doesn’t know about this – so I’m simulating a system where the loudspeaker moves around you as you rotate your head. Since this never happens in real life, it tends to break the simulation.
The stuff I showed above doesn’t include reflections, which is how you determine distance to sources. If I wanted to include reflections, each reflection would have to have its own HRTF processing, depending on its angle relative to your head.

However, hypothetically, this can work, and lots of people have tried. The easiest way to do this is to not bother measuring anything. You just take a “dummy head” -a thing that is the same size as an average human head (maybe with an average torso) and average pinnae* – but with microphones where the eardrums are – and you plunk it down in a seat in a concert hall and record the outputs of the two “ears”. You then listen to this over earphones (we don’t use headphones because we want to remove your pinnae from the equation) and you get a “you are there” experience (assuming that the dummy head’s dimensions and shape are about the same as yours). This is what’s known as a binaural recording because it’s a recording that’s done with two ears (instead of two or more “simple” microphones).

If you want to experience this for yourself, plug a pair of headphones into your computer and do a search for the “Virtual Barber Shop” video. However, if you find that it doesn’t work for you, don’t be upset. It just means that you’re different: just like everyone else.* Typically, recordings like this have a strange effect of things sounding very close in the front, and farther away as sources go to the sides. (Personally, I typically don’t hear anything in the front. All of the sources sound like they’re sitting on the back of my neck and shoulders. This might be because I have a fat head (yes, yes… I know…) and small pinnae (yes, yes…. I know…) – or it might indicate some inherent paranoia of which I am not conscious.)

* Of course, depressingly typically, it goes without saying that the sizes and shapes of commercially-available dummy heads are based on averages of measurements of men only. Neither women nor children are interested in binaural recordings or have any relevance to such things, apparently…

on to Part 2

Filters and Ringing: Part 10

There’s one last thing that I alluded to in a previous part of this series that now needs discussing before I wrap up the topic. Up to now, we’ve looked at how a filter behaves, both in time and magnitude vs. frequency. What we haven’t really dealt with is the question “why are you using a filter in the first place?”

Originally, equalisers were called that because they were used to equalise the high frequency levels that were lost on long-distance telephone transmissions. The kilometres of wire acted as a low-pass filter, and so a circuit had to be used to make the levels of the frequency bands equal again.

Nowadays we use filters and equalisers for all sorts of things – you can use them to add bass or treble because you like it. A loudspeaker developer can use them to correct linear response problems caused by the construction or visual design of the device. They can be used to compensate for the acoustical behaviour of a listening room. Or they can be used to compensate for things like hearing loss. These are just a few examples, but you’ll notice that three of the four of them are used as compensation – just like the original telephone equalisers.

Let’s focus on this application. You have an issue, and you want to fix it with a filter.

IF the problem that you’re trying to fix has a minimum phase characteristic, then a minimum phase filter (implemented either as an analogue circuit or in a DSP) can be used to “fix” the problem not only in the frequency domain – but also in the time domain. IF, however, you use a linear phase filter to fix a minimum phase problem, you might be able to take care of things on a magnitude vs. frequency analysis, but you will NOT fix the problem in the time domain.

This is why you need to know the time-domain behaviour of the problem to choose the correct filter to fix it.

For example, if you’re building a room compensation algorithm, you probably start by doing a measurement of the loudspeaker in a “reference” room / location / environment. This is your target.

You then take the loudspeaker to a different room and measure it again, and you can see the difference between the two.

In order to “undo” this difference with a filter (assuming that this is possible) one strategy is to start by analysing the difference in the two measurements by decomposing it into minimum phase and non-minimum phase components. You can then choose different filters for different tasks. A minimum phase filter can be used to compensate a resonance at a single frequency caused by a room mode. However, the cancellation at a frequency caused by a reflection is not minimum phase, so you can’t just use a filter to boost at that frequency. An octave-smoothed or 1/3-octave smoothed measurement done with pink noise might look like you fixed the problem – but you’ve probably screwed up the time domain.

Another, less intuitive example is when you’re building a loudspeaker, and you want to use a filter to fix a resonance that you can hear. It’s quite possible that the resonance (ringing in the time domain) is actually associated with a dip in the magnitude response (as we saw earlier). This means that, although intuition says “I can hear the resonant frequency sticking out, so I’ll put a dip there with a filter” – in order to correct it properly, you might need to boost it instead. The reason you can hear it is that it’s ringing in the time domain – not because it’s louder. So, a dip makes the problem less audible, but actually worse. In this case, you’re actually just attenuating the symptom, not fixing the problem – like taking an Asprin because you have a broken leg. Your leg is still broken, you just can’t feel it.

earfluff and eyecandy

audio, photography, and other stuff

Category: Digital Audio